线段树浅析及其指针式C/C++写法

线段树大家都不陌生，这也是大多数同学接触的第一个高级数据结构，总会有点谈虎色变，我就是这样，之前一直回避线段树，总觉得很难，但是明白了二进制思想后再看线段树，其实就和树状数组(树状数组简单易懂的详解)一样简单。同样地，线段树也只是一种数据结构，数据结构是一种工具，因此解决具体问题时，线段树只是一种提升时空效率的补充手段。

这里不多介绍线段树的具体细节，但给出一些我认为比较好的资源，可以看下，然后我再简单总结介绍线段树的思想，这样效果应该会比较好。

• 维基百科 - 线段树

hihoCoder上有几周专门讲了线段树，如下：

• hiho一下 第十九周
• hiho一下 第二十周
• hiho一下 第二十一周
• hiho一下 第二十二周

如果还是不怎么理解线段树，也可以参考下网上其他的教程，其实线段树说白了就是下面这幅图片：

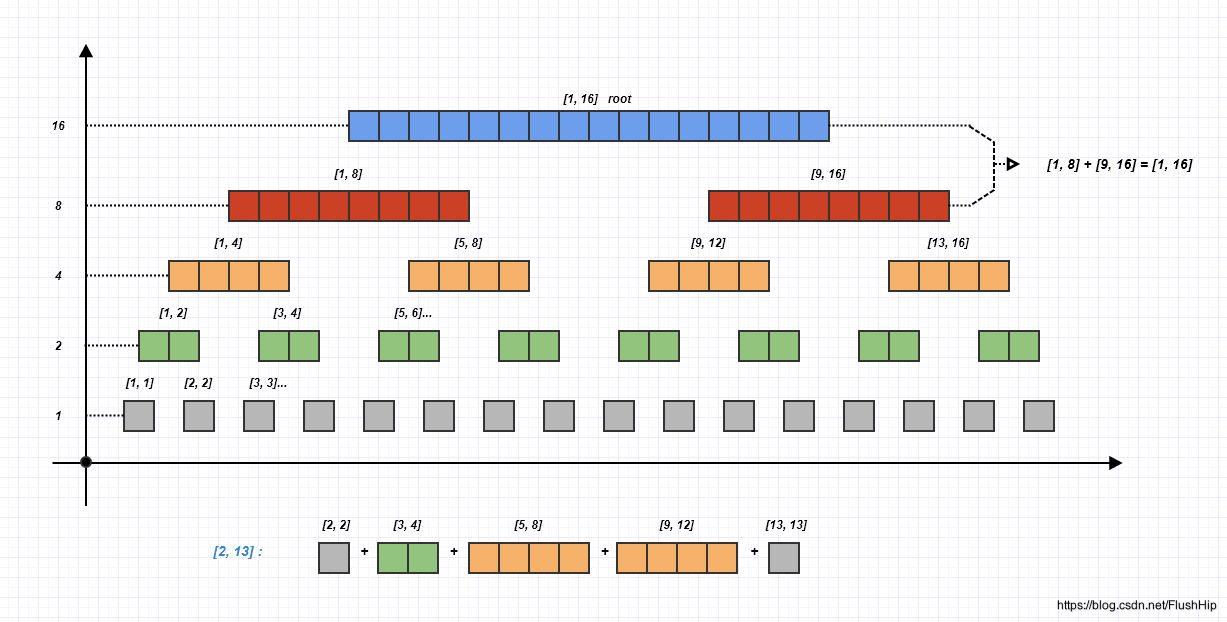
如上图所示，线段树只是帮我们预处理的一些数据，比如求区间[1, 16]的和，线段树会预处理出上图这些子区间的和，处理完之后，现在求子区间[2, 13]的和，那么就可以用到预处理的这些子区间的和，且需要的子区间的个数一定是$logn$，没错，二进制就体现在这个地方；

查询从上往下，那么更新就要从下往上，因为修改了[1, 1]就一定要修改[1, 2], [1, 4], [1, 8], [1, 16]。因此修改的子区间个数也一定是$logn$，因为树高就是$logn$。

线段树的思想就讲完了，精髓还是在图中。说了这么多，线段树在代码中改怎么写呢，大多数时候是以开数组的方式来写的，这种方式好调试，同时也易理解，确实是ACM竞赛中的常青树，但数组式需要多开空间来预防越界风险，当然肯定有不多开空间的方式，这里就不多说了。

而我比较喜欢用指针式的，指针式的好处和数组式反的。下面就来介绍下指针式的写法及其坑点。

结点的数据结构

typedef struct Node {int data;Node *lchs, *rchs;Node (int data = 0, Node *lchs = nullptr, Node *rchs = nullptr) :data(data), lchs(lchs), rchs(rchs) {}~Node() {if (lchs != nullptr)delete lchs;if (rchs != nullptr)delete rchs;}
} *pNode;

• data域就是你要维护的数据，这里我举个例子假设这个data是一个int变量，当然你可以维护不止一个变量；

• lchs和rchs就是结点的左右孩子，都是指向自己的指针类型；

• 写一个构造函数，这个用来建树的时候新建结点赋初值用；

• 为结点指针重定义一个类型pNode，这样在后续函数的形参中可以方便使用这个指针。

• 写一个析构函数，这是为了在多组样例的情况下，能及时释放这颗线段树而不造成内存泄漏，或者你也可以不写析构函数，直接写一个递归函数去释放整颗线段树的内存，类似这样：

  void fail(pNode root)
  {if (root == nullptr)return ;fail(root->lchs);fail(root->rchs);delete root;
  }
  

写析构函数同样能完成这个递归的操作，而且逻辑会清晰很多。

其实这里有更好的做法，C++11的库中出现了智能指针std::shard_ptr，我们可以用这个来代替裸指针，这样子我们不用写析构函数，同时也不用写递归函数了。做法如下：

struct Node {int data;std::shared_ptr<Node> lchs, rchs;Node (int data = 0, std::shared_ptr<Node> lchs = nullptr, std::shared_ptr<Node> rchs = nullptr) :data(data), lchs(lchs), rchs(rchs) {}
};

这样子的做法更简洁。

线段树的基本操作就是

• 建树(build)
• 查询(query)
• 更新(update)

下面有三道例题，可以试做一下，然后没事多对应代码看看上面图片，现在所有的操作都是建立在区间查询，单点更新的基础上，这也是线段树最常用的场景之一，关于线段树其余的操作，比如lazy标记等等，自行学习。

模板题

题面：

给出长度为$n(<10^5)$的序列$a$，$m(<10^5)$次操作，add i j表示$a[i]+=j$；query i j表示询问求子序列$a[i,j]$的和，不用考虑溢出问题。

nclude <iostream>
#include <memory>
#include <string>template<typename T>
struct SgTreeNode;template<typename T>
using spSgTreeNode = std::shared_ptr<SgTreeNode<T>>;template<typename T>
struct SgTreeNode
{T data;spSgTreeNode<T> lchs, rchs;struct SgTreeNode(const T & data, spSgTreeNode<T> lchs = nullptr, spSgTreeNode<T> rchs = nullptr): data(data), lchs(lchs), rchs(rchs){}
};template<typename T>
void build(spSgTreeNode<T> & root, uint32_t lCount, uint32_t rCount)
{root = std::make_shared<SgTreeNode<T>>(0);if (lCount == rCount) return;uint32_t mid = lCount + (rCount - lCount) / 2;build(root->lchs, lCount, mid);build(root->rchs, mid + 1, rCount);
}template<typename T>
T query(spSgTreeNode<T> root, uint32_t lCount, uint32_t rCount, uint32_t lPoint, uint32_t rPoint)
{if (lCount == lPoint && rCount == rPoint) return root->data;uint32_t mid = lCount + (rCount - lCount) / 2;if (rPoint <= mid) return query(root->lchs, lCount, mid, lPoint, rPoint);else if (lPoint >= mid) return query(root->rchs, mid + 1, rCount, lPoint, rPoint);else return query(root->lchs, lCount, mid, lPoint, mid) + query(root->rchs, mid + 1, rCount, mid + 1, rPoint);
}template<typename T>
void update(spSgTreeNode<T> root, uint32_t lCount, uint32_t rCount, uint32_t targetPosition, uint32_t value)
{root->data += value;if (lCount == rCount) return;uint32_t mid = lCount + (rCount - lCount) / 2;if (targetPosition <= mid) update(root->lchs, lCount, mid, targetPosition, value);else update(root->rchs, mid + 1, rCount, targetPosition, value);
}int main()
{for (uint32_t n, m; std::cin >> n >> m; ){spSgTreeNode<uint64_t> root = nullptr;build(root, 1, n);for (uint32_t i = 0; i < n; ++i){uint32_t value;std::cin >> value;update(root, 1, n, i + 1, value);}for (uint32_t loop = 0; loop < m; ++loop){std::string str;uint32_t i, j;std::cin >> str >> i >> j;if (str == "query") std::cout << query(root, 1, n, i, j) << std::endl;else update(root, 1, n, i, j);}}return 0;
}

hihoCoder1116 - hihoCoder挑战赛8 - 计算

题目链接：点这儿。

#include <bits/stdc++.h>using namespace std;const int mod = 10007;typedef struct Node {int sum, product;int pre, suf;Node *lchs, *rchs;Node (int sum = 0, int product = 0, int pre = 0, int suf = 0, Node *lchs = nullptr, Node *rchs = nullptr) :sum(sum), product(product), pre(pre), suf(suf), lchs(lchs), rchs(rchs) {}
} *pNode;void build(pNode &root, int l, int r)
{root = new Node();if (l == r)return ;int mid = (l + r) >> 1;build(root->lchs, l, mid);build(root->rchs, mid + 1, r);
}void update(pNode root, int l, int r, int index, int x)
{if (l == r) {root->sum = root->product = root->pre = root->suf = x % mod;return ;}int mid = (l + r) >> 1;if (index <= mid)update(root->lchs, l, mid, index, x);elseupdate(root->rchs, mid + 1, r, index, x);root->sum = (root->lchs->sum + root->rchs->sum + root->lchs->suf * root->rchs->pre % mod) % mod;root->product = root->lchs->product * root->rchs->product % mod;root->pre = (root->lchs->pre + root->lchs->product * root->rchs->pre % mod) % mod;root->suf = (root->rchs->suf + root->rchs->product * root->lchs->suf % mod) % mod;
}void fail(pNode root)
{if (root == nullptr)return ;fail(root->lchs);fail(root->rchs);delete root;
}int main()
{for (int n, q; EOF != scanf("%d%d", &n, &q); ) {pNode root = nullptr;build(root, 1, n);for (int i = 0, index, x; i < q; i++) {scanf("%d%d", &index, &x);update(root, 1, n, index, x);printf("%d\n", root->sum);}fail(root);}return 0;
}

POJ3368 - Frequent values

题目链接：点这儿。

51NOD1199 - Money out of Thin Air

题目链接：点这儿。

这个题看起来在树上操作，但是，如果你把树转换成先序遍历序列(树的先序遍历序列和后序遍历序列，子树节点都挨在一起，类似RootLeftRight)，那么树就成了区间。对节点的操作就变成了点修改与点查询，对子树的操作就变成了区间修改与区间查询。

在对树的先序遍历过程中给每个节点加上时间戳，并统计好每个节点的子孙数；

查询的时候只要根据节点找到对应时间戳，这个时间戳是查询与修改区间的左端点，查询与修改区间的长度就是该子树的子孙数加一(点修改区间长度为一)。

由于是区间修改，因此加上lazy标记。

#include <bits/stdc++.h>using namespace std;using LL = long long;int n, m;
int num;vector< vector<int> > childs;
vector<int> weight, foundation;vector<int> allSons;
vector<int> indexs;typedef struct Node *pNode;struct Node {LL sum;LL lazy;pNode lchs, rchs;Node(LL sum = 0, LL lazy = 0, pNode lchs = nullptr, pNode rchs = nullptr) : sum(sum),lazy(lazy),lchs(lchs),rchs(rchs) {}~Node() {if (lchs != nullptr)delete lchs;if (rchs != nullptr)delete rchs;}
};int dfs(int root)
{indexs[root] = num++;allSons[root] = 0;for (auto to : childs[root]) {allSons[root] += dfs(to);}return allSons[root] + 1;
}void build(pNode &root, int l, int r)
{root = new Node;if (l + 1 == r) {root->sum = weight[foundation[l]];return ;}int mid = (l + r) >> 1;build(root->lchs, l, mid);build(root->rchs, mid, r);root->sum = root->lchs->sum + root->rchs->sum;
}LL query(pNode root, int l, int r, int a, int b)
{root->sum += (r - l) * root->lazy;if (r - l != 1) {root->lchs->lazy += root->lazy;root->rchs->lazy += root->lazy;}root->lazy = 0;if (l == a && r == b)return root->sum;int mid = (l + r) >> 1;LL ret = 0;if (b <= mid)ret += query(root->lchs, l, mid, a, b);else if (a >= mid)ret += query(root->rchs, mid, r, a, b);elseret += query(root->lchs, l, mid, a, mid) +query(root->rchs, mid, r, mid, b);return ret;
}bool update(pNode root, int l, int r, int a, int b, int tag)
{if (l == a && r == b) {root->lazy += tag;return true;}root->sum += (b - a) * tag;int mid = (l + r) >> 1;if (b <= mid)update(root->lchs, l, mid, a, b, tag);else if (a >= mid)update(root->rchs, mid, r, a, b, tag);elseupdate(root->lchs, l, mid, a, mid, tag),update(root->rchs, mid, r, mid, b, tag);return true;
}int main()
{for (; EOF != scanf("%d%d", &n, &m); ) {childs.clear();childs.resize(n + 1);weight.resize(n + 1);weight[1] = 0;allSons.resize(n + 1, 0);indexs.resize(n + 1);foundation.resize(n + 1);for (int i = 2, w, p; i <= n; ++i) {scanf("%d%d", &p, &w);childs[p + 1].push_back(i);weight[i] = w;}num = 1, dfs(1);for (int i = 1; i < n + 1; foundation[indexs[i]] = i, ++i) {}pNode root = nullptr;build(root, 1, n + 1);for ( ; m--; ) {char C[2];int x, y, z;scanf("%s%d%d%d", C, &x, &y, &z);++x;if (C[0] == 'S') {query(root, 1, n + 1, indexs[x], indexs[x] + 1) < 1LL * y ? update(root, 1, n + 1, indexs[x], indexs[x] + 1, z) : true;} else {query(root, 1, n + 1, indexs[x], indexs[x] + allSons[x] + 1) < 1LL * y * allSons[x] + y ? update(root, 1, n + 1, indexs[x], indexs[x] + allSons[x] + 1, z) : true;}}for (int i = 1; i <= n; ++i)printf("%lld\n", query(root, 1, n + 1, indexs[i], indexs[i] + 1));if (root != nullptr)delete root;}return 0;
}

51NOD1287 - 加农炮

题目链接：点这儿。

我把这个题题面意思换了一下，做成了中南林业科技大学第十一届程序设计竞赛的J题，参见中南林业科技大学第十一届程序设计大赛 - 题解。