本文主要是介绍耶鲁博弈论笔记,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
编辑记录:
1126:开个新坑,耶鲁大学的博弈论课程, 和专业相关不大,纯兴趣,尽量写好一点吧
1.
首先指出博弈论是一种研究策略形式的方法,对于经济学中,完全竞争市场只能被动接受均衡价格,而垄断市场也不用考虑策略,只有处在之中的完全垄断和完全竞争之间的参与者需要面对策略形势
此外,策略形式下的参与者受到的影响既取决于自身行为,也取决于其他参与者的动作
1.1 积分游戏
- 积分游戏的规则就是下图,我和伙伴的选择决定了分数的多少
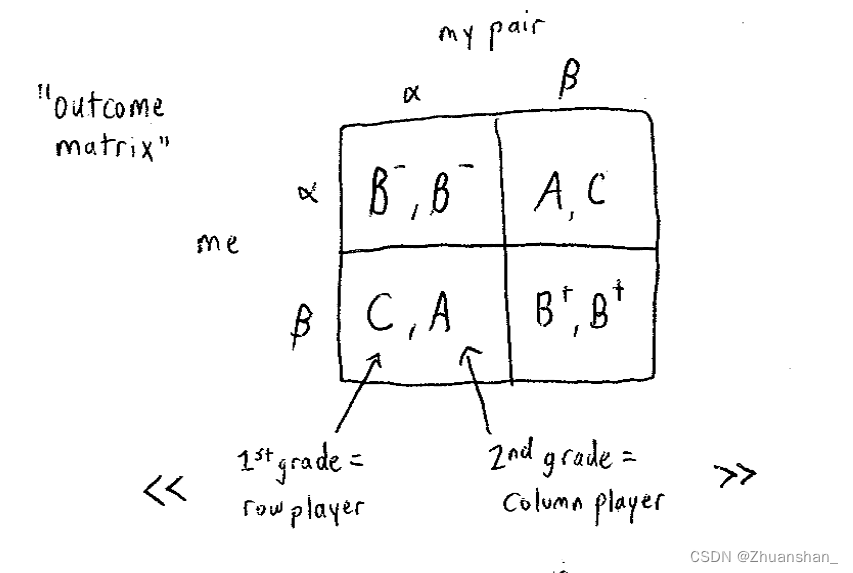
将表格画出后,引出了新的问题,即对于玩家的选择取决于什么呢?即需要一个分数来量化这一选择和结果,那么我们按照“分奴”的想法进行量化,重新画出矩阵
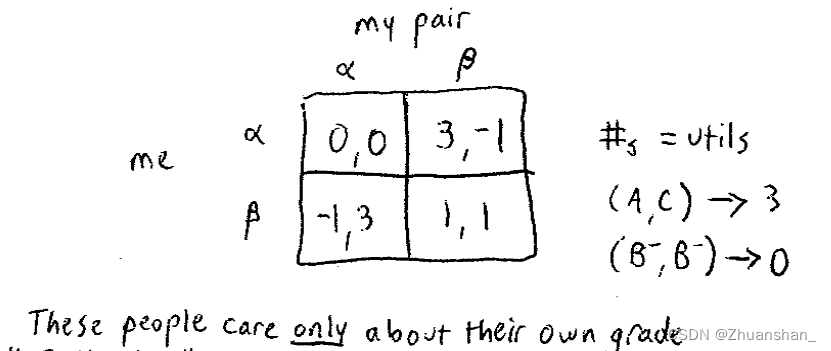
此时,再看这个矩阵就变成了数字比大小的游戏了
因此,从我的角度来看,假设对手选a,那么我选a的得分要比b高——0>-1,而假设对手选b,那么我选a的得分也要比b高——3>1,因此,无论如何,我都要选a
这里,我们引出第一个定义:
严格优势策略 Strictly Dominant Strategy
Def: We say that my strategy α strictly dominates my strategy β if my payoff from α is strictly greater than that from β regardless of what others do.
即a策略的收益在无论对手作何对应的情况下都高于b的策略的收益,则可以说a相对于b为严格优势策略
从定义,我们推导出第一个结论:
Lesson1:不要使用严格优势策略
在游戏中,大家都是理性人,都会追求更高的数字,因此,都选择a时,结果为(0,0),而双方都选b时,结果为(1,1),因此,可以推出结论2
Lesson2:理性选择可能导致更糟的结果
这种囚徒困境的例子还有很多,如宿舍打扫卫生、企业之间的价格战等
如何破解囚徒困境,常见的方法是沟通、但缺乏强制力的情况下,沟通缺乏意义
接下来,我们考虑隔壁神学院的学生会作何选择,他们不再属于分奴,而是会在道德层面上考虑问题
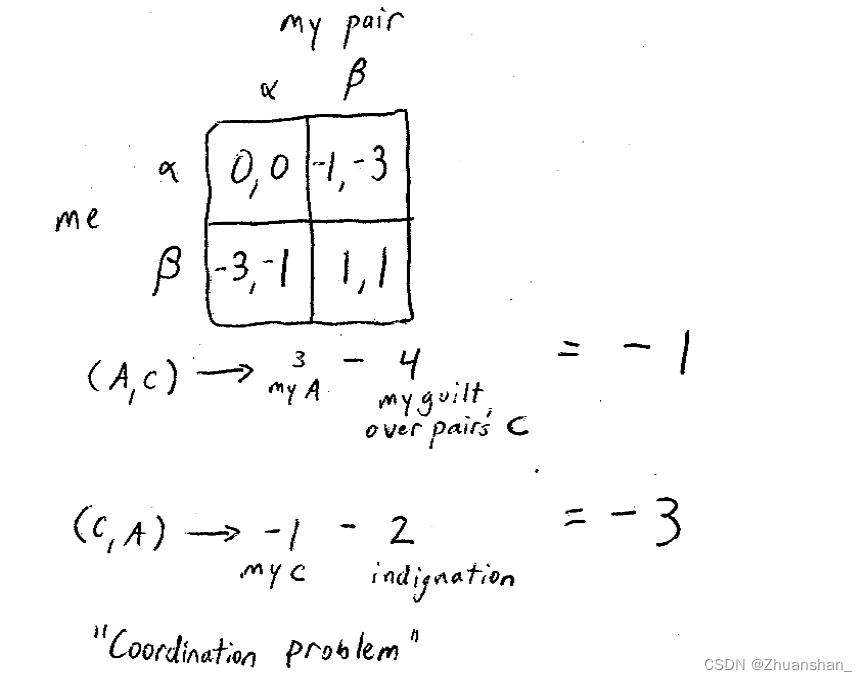
这种情况下,若两位出现了(a,b)组合,则选择a的同学会得到3分,但是因为背叛的罪恶感产生-4的收益,最后变成-1, 原本选择b的同学获得-1的收益,但是他对对方的背叛很生气,产生了-2的情绪收益,最后总体为-1-2=-3
因此两位同学之间就存在了协和谬误(Coordination Problem),a也不再是严格优势策略
这里,得出第三个结论,如果我们不知道一个人或一场博弈中的收益情况,那么就不可能获得收益
Lesson3:汝欲得之,必先知之
参考资料
- 学习博弈论,从入门、进阶到精通,如何列书单?
- 耶鲁大学 博弈论(Game Theory) 笔记1
这篇关于耶鲁博弈论笔记的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







