【TransCad】通过四阶段法进行交通需求预测——1.梳理四阶段法的“前因后果”

前言

道路交通计算机辅助课程接近尾声了，今天学了下怎么利用TC进行交通分配。在具体介绍软件操作前，我想先理一理交通规划四阶段法的前因后果。

交通生成（Trip Generation）

我们知道，在城市规划中，不同的用地有不同的性质，如居住用地的居住性质和工业用地的工作性质等。也这是这些不同的土地利用性质，人们产生了交通需求，如上班、购物等活动。

引用《TransCAD交通需求模型手册》里的话，任何基于家庭的出行被认为是从家庭端产生的，任何不基于家庭的出行被认为是从起始点产生的，而任何以家庭之外的活动场所为目的地的出行被认为是被该场所吸引。

我们把这个场所就当做我们的交通小区（TAZ），那么，该如何预测某一小区会有多少交通量发生，又会有多少交通量吸引呢？

我们一般采用回归方程法，也就是通过大量数据，建立起交通发生量/吸引量，与一些自变量如人口、岗位等的函数关系。这样如果我们预测出了这些自变量，代入我们得到的回归方程，即可求出预测的交通量。

举个栗子，以现在时间2023年为起始，来预测z小区2030年的交通发生\吸引量。

假设交通发生量只与小区的人口有关，而交通吸引量只与小区的岗位数有关。我们调查到了现在2023年的数据（包括每个小区的人口、岗位、交通发生和交通吸引量），我们便可以建立起交通发生\吸引与人口\岗位的函数关系。接着我们只需预测出z小区2030年的人口、岗位，即可求出z小区2030年的交通发生、吸引量。

交通分布（Trip Distribution）

一般来说，现状小区之间的OD量我们通过调查是可以得到的，然后通过上一步的交通生成，我们也有了各小区未来年的发生、吸引量（PA数据）。不过这个PA数据这是某一小区总的发生、吸引量，具体是前往哪个小区和来自哪个小区是不知道的，而这也是需要进行交通分布预测的原因。预测的结果，是各小区之间未来年的OD量。

实现方法之一的增长系数法在我的另一篇博客中有介绍。比较常用的重力模型法，我的这篇——博客有软件操作部分。那我这里提一提我对重力模型法的一点理解。

重力模型法

我这里仅做不严谨的理解。

重力模型法预测考虑了两个交通小区的吸引强度和它们之间的阻力，认为两个交通小区的出行吸引与两个交通小区的出行发生量与吸引量成正比，而与交通小区之间的阻抗成反比。一般可以表示为：
$$q_{ij}=k{P}_i{A}_{j}f(c_{ij})$$

我们可以仿照上一部分交通生成讲过的回归方程法，其实这也是用的回归法来标定里面这些参数。只是这里的稍微复杂些。

这里的P和A就是我们第一步交通生成的交通发生和吸引量（已知），而后面是阻抗函数，一般是关于时间和饱和度的函数，我们可以先不管，因为软件里面会帮我们计算出来，我们只需输入一些参数的值即可。下面是手册里的一些推荐值：

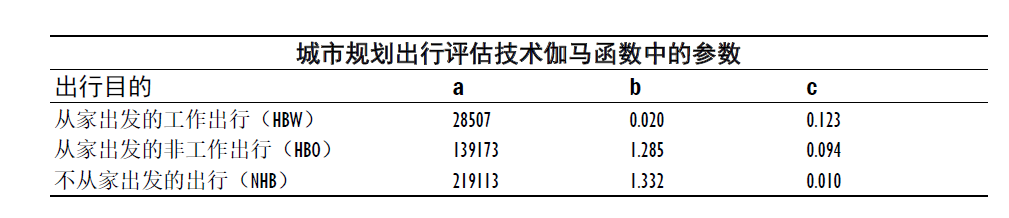
一般我们只需要通过建立路网，得出各个小区的之间的最短通行时间矩阵，再结合平衡后的PA数据，即可完成重力模型分布预测。

交通分配（Traffic Assignment）

好了，通过交通分布，我们未来年的OD也求出来了。但是这只是各个小区之间的交通量，具体这些车辆会走哪条路上还不知道。现在要做的就是把这些OD给它分配到现状的具体路网上去，看看现状的路网能不能支撑未来的交通量。

实际上交通分配前还有一个方式划分（Modal Spilt）,但老师讲那个需要的数据较多，就跳过了。后面有空我自己补上吧。

怎么分呢？国际上通常将交通分配方法分为平衡模型与非平衡模型两大类，并以Wardrop第一、第二原理为划分依据。

• Wardrop第一原理：网络上的交通以这样一种方式分布，就是使所有使用的路线都比没有使用的路线费用小。
• Wardrop第二原理：车辆在网络上的分布，使得网络上所有车辆的总出行时间最少。

满足第一原理的模型称为用户平衡模型（UE,User-Optimized Equilibrium），满足第二原理的称为系统最优模型（SO,System-Optimized Equilibrium），若不使用 Wardrop 原理，则该模型为非平衡模型。

UE模型

1956年Beckmann提出了一种满足Wardrop第一原理的数学规划模型，其核心是交通网络中的用户都试图选择最短路径，而最终使被选择的路径的阻抗最小且相等。

具体数学表达我就不展示了，TC中采用的是 Frank-Wolf 算法进行求解，其步骤如下：

SO模型可通过转换为用户平衡模型来进行求解。除此之外，TC中还可以采用SUE（随机用户平衡法，Stochastic User Equilibrium）来进行分配。

非平衡分配方法

非平衡模型具有结果简单、概念明确、计算简便等优点。

长期以来，多种多样的交通分配模型已经得到开发与应用。许多较为过时的交通分配方法存在很多缺点，应当被新的方法取代而不再应用。但是，在TransCAD 中仍保留了这些过时的模型，以便用户已经建立的模型不需要任何改进就可以在TransCAD中使用，或许这些模型还可以用于学术研究。

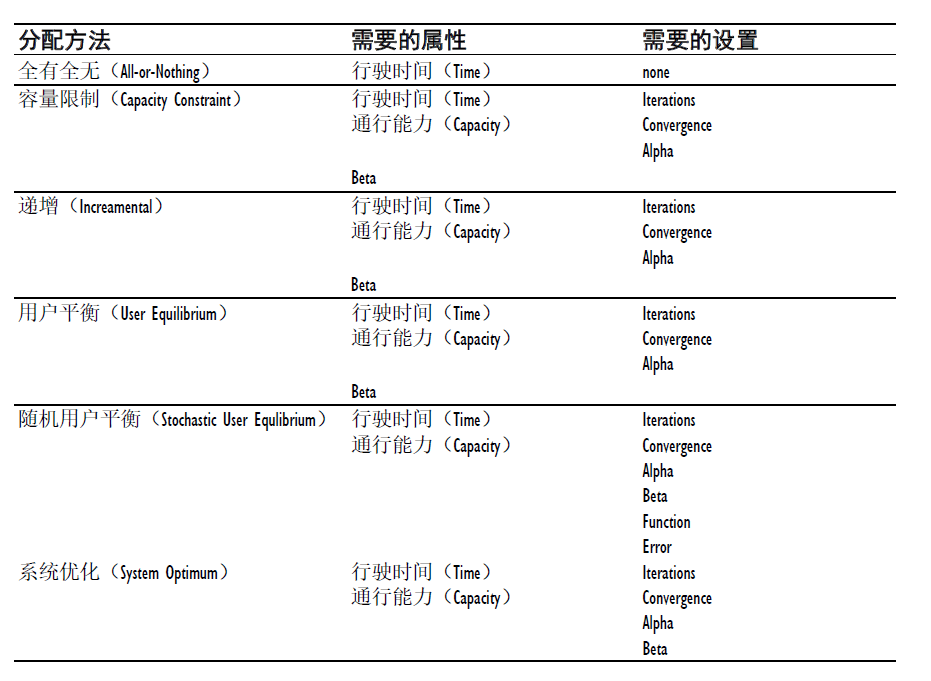
TC中每种分配方法的设置要求如下：

总结

以上就是四阶段法（准确来说是三阶段）在进行交通需求预测时的前因后果，这些也是正确进行软件操作的前提。如果基本原理不去梳理清楚的话，尽管最后凭借记忆和笔记在软件中实现了操作，也仅仅是表面功夫。

我们进行软件操作需要准备的有：

1. 现状路网和小区
2. 各小区的现状人口、岗位以及OD数据
3. 各小区未来的人口、岗位以及PA数据

具体的软件实操部分就放在下一篇博客，我们下期见。