本文主要是介绍数据结构与算法——图篇详解,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目 录
- 1. 图
- 1.1 基本概念
- 1.1.1 顶点与边
- 1.1.2 无向图
- 1.1.3 有向图
- 1.1.4 权和网
- 1.1.5 完全图
- 1.1.6 稠密图和稀疏图
- 1.1.7 子图和生成子图
- 1.1.8 邻接点
- 1.1.9 顶点的度
- 1.1.10 路径与回路
- 1.1.11 连通图和连通分量
- 1.1.12 强连通图和强连通分量
- 1.1.13 生成树和生成森林
- 1.2 图的抽象数据类型
- 1.3 图的存储结构
- 1.3.1 图的类型&存储结构
- 1.3.2 邻接矩阵:定义
- 1.3.3 邻接矩阵:类的描述
- 1.3.4 邻接矩阵:基本操作
- 1)创建图
- 2)创建无向网
- 3)创建有向网
- 4)顶点定位
- 5)查询第一个邻接点
- 6)查找下一个邻接点
- 1.3.5 邻接表:定义
- 1.3.6 邻接表:相关类
- 1.3.6 邻接表:基本操作
- 1)创建无向网
- 2)创建有向网
- 3)顶点定位
- 4)插入边
- 5)第一个邻接点
- 6)查询下一个邻接点
- 1.3.7 练习
- 1.4 图的遍历
- 1.4.1 广度优先搜索
- 1)定义
- 2)算法分析
- 3)算法实现
- 4)性能分析
- 1.4.2 深度优先搜索
- 1)定义
- 2)算法分析
- 3)算法实现
- 4)性能分析
- 1.4.3 练习
- 1)例1
- 2)例2
- 1.5 最小生成树
- 1.5.1 基本概念
- 1)树的特性
- 2)最小生成树
- 1.5.2 克鲁斯卡尔(Kruskal)算法
- 1)概述
- 2)算法分析
- 3)性能分析
- 1.5.3 普里姆(Prim)算法
- 1)概述
- 2)算法分析
- 3)步骤分析
- 4)代码实现
- 5)性能分析
- 1.5.4 两个算法对比
- 1.5.5 练习
- 1.6 最短路径
- 1.6.1 某个顶点到其余各顶点的最短路径
- 1)概述
- 2)实例
- 3)迪杰斯特拉(Dijkstra)算法:概述
- 4)迪杰斯特拉(Dijkstra)算法:算法分析
- 5)迪杰斯特拉(Dijkstra)算法:代码实现
- 6)迪杰斯特拉(Dijkstra)算法:性能分析
- 7)练习
- 1.6.2 每一对顶点之间的最短路径
- 1)概述
- 2)佛洛依德(Floyed) 算法:概述
- 3)佛洛依德(Floyed) 算法:算法分析
- 4)佛洛依德(Floyed) 算法:代码实现
- 5) 练习
- 1.7 拓扑排序
- 1.7.1 拓扑排序:基本概念
- 1.7.2 拓扑排序:分析
- 1.7.3 拓扑排序:步骤
- 1.7.4 拓扑排序:实现
- 1.7.5 拓扑排序:性能分析
- 1.7.6 练习
- 1.8 关键路径
- 1.8.1 现实问题
- 1.8.2 相关概念
- 1.8.3 算法分析
- 1.8.4 算法步骤
- 1.8.5 算法实现
- 后记
1. 图
- 图 Graph 是一种更为复杂的数据结构,图形结构中,每一个数据元素都可以和其他任意的数据元素相关。
1.1 基本概念
1.1.1 顶点与边
-
图是有
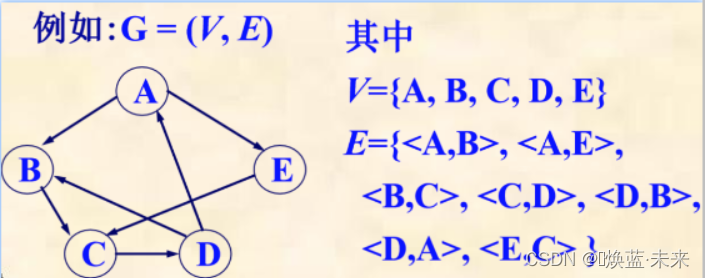
顶点集和边集组成。- 图:一般使用G表示
- 顶点集:一般使用V表示,是一个有穷非空集合。由
顶点组成,例如:u,v 等顶点。 - 边集:一般使用E表示,是一个有穷集合,可以是空集。由
边组成,例如:e等边。 - 记作:G = (V, E)
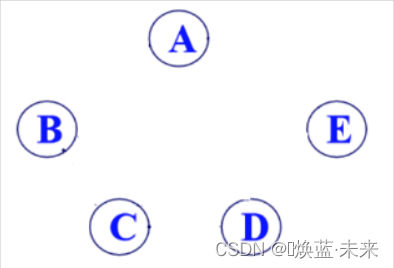
- 零图:E可以是空集,此时图G只有顶点没有边,称为零图。
-
例如:
-
零图:
1.1.2 无向图
-
无向边:顶点u和顶点v,在没有方向的情况下形成的边,简称为边。
- 记作:(u, v) = (v, u),也就是 (u, v) 和 (v, u) 是等同的。
-
无向图(Undirected Graph):全部由无向边构成的图。
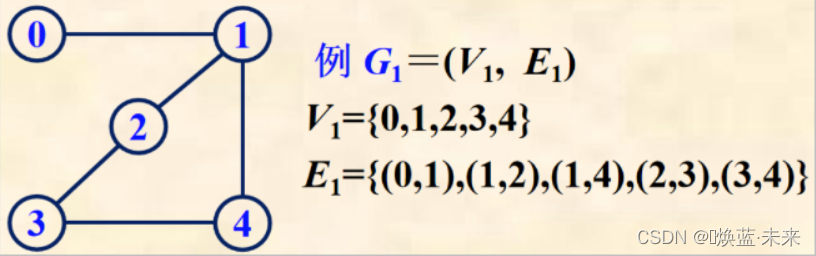
1.1.3 有向图
-
有向边:按照方向,从顶点u到顶点v形成的边,简称为弧。
- 记作:<u, v>、<v, u> ,也就是<u, v> 和 <v, u> 是不同的。
- 顶点u称为始点(Initial Node),或弧尾(Tail)。
- 顶点v称为终点(Terminal Node),或弧头(Head)。
-
有向图(Directed Graph):全部由有向边构成的图。

1.1.4 权和网
- 权(Weight):在一个图中,每条边可以标上具有某种含义的数值,此数值称为该边上的权。
- 通常权是一个非负实数。
- 权可以表示从一个顶点到另一个顶点的距离、时间或代价等含义。
- 网(Network):边上标识权的图。

1.1.5 完全图
-
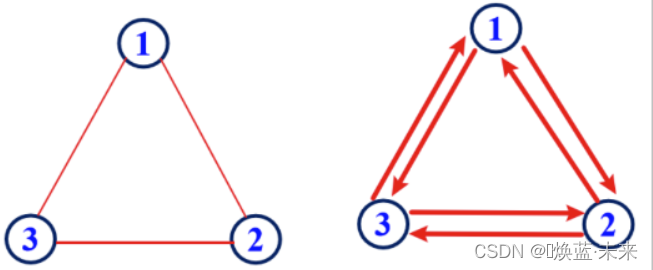
无向完全图:每两个顶点之间都存在一条边。

-
有向完全图:每两个顶点之间都存在着方向相反的两条边。
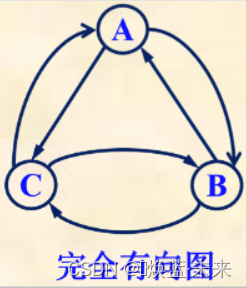
-
完全图有n个顶点,e条边,两者关系:
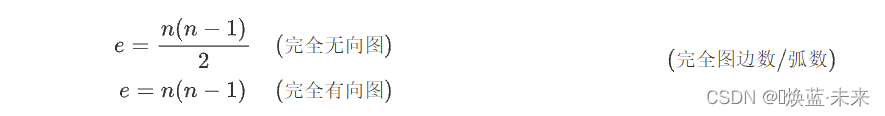
1.1.6 稠密图和稀疏图
- 在具有n个顶点、e条边的图G中,若含有较少的边,称为图G为稀疏图(Sparse Graph)。
- 反之称为稠密图(Dense Graph)


1.1.7 子图和生成子图
- 子图(Subgraph)
- 设有两个图 G=(V, E) 和 G’=(V’, E’),若V‘是V的子集,即V’ ∈ V,并且E‘ 是 E的子集,即E’ ∈ E,则称 G‘ 为G的子图,记为 G’ ∈ G。
- 生成子图(Spanning Subgraph)
- 若G‘ 为G的子图,并且V’ = V,则称G‘ 为G的生成子图,即包含原图中所有顶点的子图。

1.1.8 邻接点
-
在一个无向图中,若存在一条边(u,v),则称顶点u与v互为邻接点。
-
边(u,v)是顶点u和v关联的边
-
顶点u和v是边(u,v)关联的顶点。
-
例如:以
顶点1为端点的3条边是(0,1),(1,2),(1,4),顶点1的3个邻接点分别为0,2,4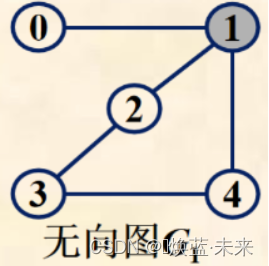
-
-
在一个有向图中,若存在一条弧<u,v>,则称顶点u邻接到v,顶点v邻接自u。
-
弧<u,v>和顶点u、v关联。
-
例如:顶点v0有2条出边<v0,v1>,<v0,v2>,1条入边<v3,v0>,顶点v0邻接到v1和v2,顶点v0邻接自v3
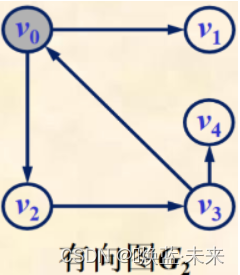
-
1.1.9 顶点的度
-
顶点的度(Degree):图中与该顶点相关联边的数目。顶点v的度记为 D(v)。
-
若一个图有n个顶点和e条边,则该图
所有顶点的度之和与边数满足如下关系:
e = 1 2 ∑ i = 0 n − 1 D ( v i ) ( ) e = \frac{1}{2}\sum_{i=0}^{n-1}D(v_i) \tag{} e=21i=0∑n−1D(vi)()- 每条边关联两个顶点,对顶点的度贡献为2,所有全部顶点的度之和为所有边数的2倍。
-
无向图顶点的度:以该顶点为一个端点的边的数目,即该顶点的边的数目。
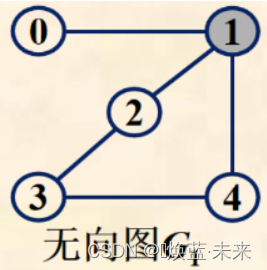
D ( 0 ) = 1 D ( 1 ) = 3 D ( 2 ) = 2 D ( 3 ) = 2 D ( 4 ) = 2 e = 1 2 ∑ i = 0 n − 1 D ( v i ) = 1 + 3 + 2 + 2 + 2 2 = 5 ( ) D(0)=1 \\ D(1)=3 \\ D(2)=2 \\ D(3)=2 \\ D(4)=2 \\ e = \frac{1}{2}\sum_{i=0}^{n-1}D(v_i) = \frac{1+3+2+2+2}{2} = 5 \tag{} D(0)=1D(1)=3D(2)=2D(3)=2D(4)=2e=21i=0∑n−1D(vi)=21+3+2+2+2=5()
-
有向图顶点的度
- 入度(in degree):顶点v的入边数目,称为该顶点的入度,记为 ID(v)。
- 以v为终点的弧的数目称为入度。
- 出度(out degree):顶点v的出边数目,称为该顶点的出度,记为 OD(v)。
- 以v为起点的弧的数目称为出度。
- 顶点v的度:等于它的入度和出度之和。记作 D(v) = ID(v) + OD(v)
- 入度(in degree):顶点v的入边数目,称为该顶点的入度,记为 ID(v)。
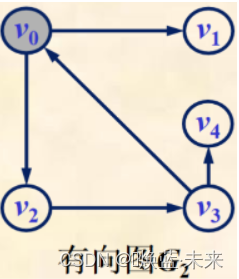
D ( v 0 ) = I D ( v 0 ) + O D ( v 0 ) = 1 + 2 = 3 D ( v 1 ) = I D ( v 1 ) + O D ( v 1 ) = 1 + 0 = 1 D ( v 2 ) = I D ( v 2 ) + O D ( v 2 ) = 1 + 1 = 2 D ( v 3 ) = I D ( v 3 ) + O D ( v 3 ) = 1 + 2 = 3 D ( v 4 ) = I D ( v 4 ) + O D ( v 4 ) = 1 + 0 = 1 e = 1 2 ∑ i = 0 n − 1 D ( v i ) = 3 + 1 + 2 + 3 + 1 2 = 5 ( ) D(v_0) = ID(v_0) + OD(v_0) = 1 + 2 = 3 \\ D(v_1) = ID(v_1) + OD(v_1) = 1 + 0 = 1 \\ D(v_2) = ID(v_2) + OD(v_2) = 1 + 1 = 2 \\ D(v_3) = ID(v_3) + OD(v_3) = 1 + 2 = 3 \\ D(v_4) = ID(v_4) + OD(v_4) = 1 + 0 = 1 \\ e = \frac{1}{2}\sum_{i=0}^{n-1}D(v_i) = \frac{3+1+2+3+1}{2} = 5 \tag{} D(v0)=ID(v0)+OD(v0)=1+2=3D(v1)=ID(v1)+OD(v1)=1+0=1D(v2)=ID(v2)+OD(v2)=1+1=2D(v3)=ID(v3)+OD(v3)=1+2=3D(v4)=ID(v4)+OD(v4)=1+0=1e=21i=0∑n−1D(vi)=23+1+2+3+1=5()
1.1.10 路径与回路
-
路径(Path):在一个图中,路径是从顶点u到顶点v所经过的顶点序列。
u=vi0,vi1,…vim = v
-
路径长度:该路径上边的数目。
-
回路:第一个顶点和最后一个顶点相同的路径,称为回路或环。
-
初等路径:序列中顶点不重复出现的路径。
-
初等回路:除了第一个顶点和最后一个顶点之外,其余顶点不重复出现的回路。
-
实例1:
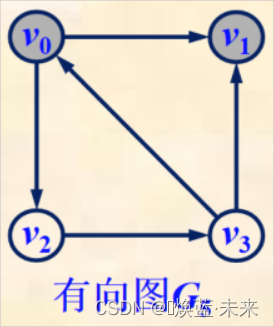
路径 (v0, v2, v3, v1) 是初等路径,其路径长度为3。
路径 (v0, v2, v3, v0, v1) 不是初等路径,其路径长度为4。
路径 (v0, v2, v3, v0) 是初等回路,其路径长度为3。
-
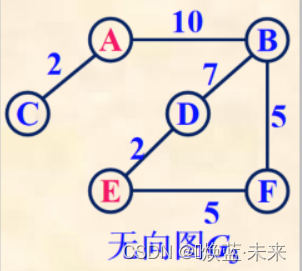
网中的路径长度:在网中,从始点到终点的路径上各边的权值之和,称为路径长度。
-
实例2:从
顶点A到顶点E的一条路径(A, B, D, E) --> 路径长度:10 + 7 + 2 = 19
-
1.1.11 连通图和连通分量
-
连通:在无向图中,若从顶点u到顶点v有路径,则称u和v是连通的。
-
连通图:若无向图中的任意两个顶点均是连通的,则称该图是连通图。

-
连通分量:若无向图为非连通图,则图中各个
极大连通子图称为此图的连通分量。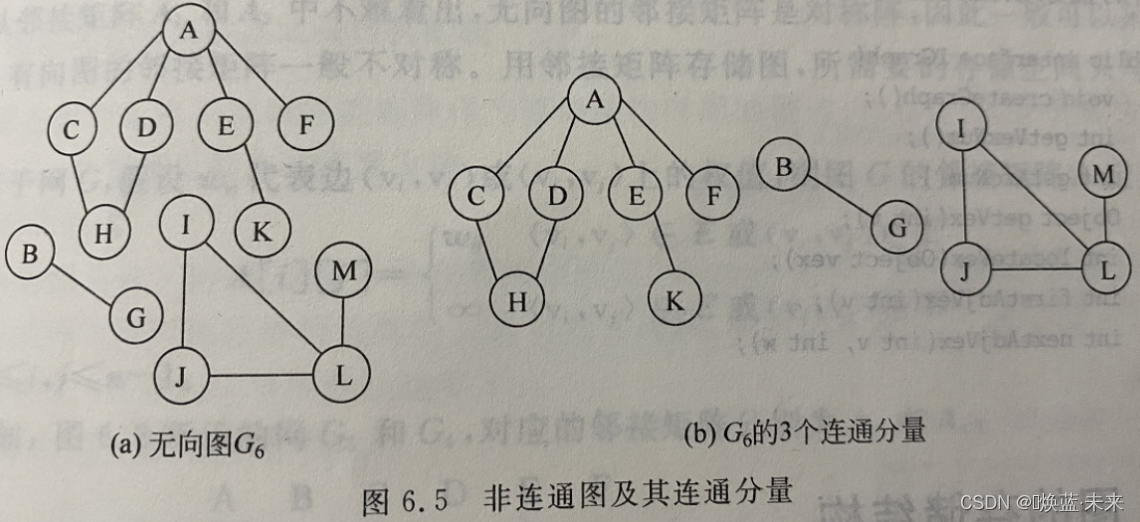
1.1.12 强连通图和强连通分量
-
强连通图:在有向图中,若任意两个顶点均连通(一条有向路径),则称该图是强连通图。
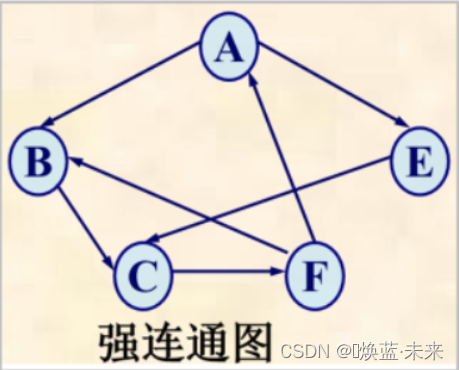
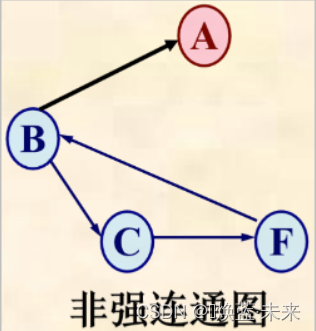
-
强连通分量:有向图中的
极大强连通子图。强连通图只有一个强连通分量,即其本身。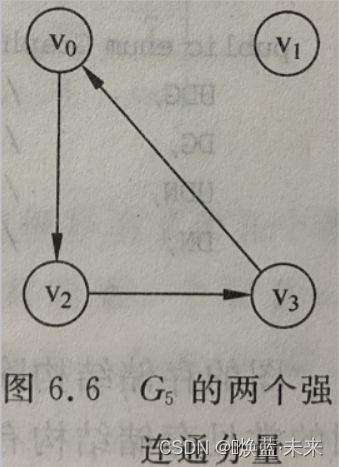
1.1.13 生成树和生成森林
-
生成树:假设一个连通图有n个顶点和e条边,其中
n-1条边和n个顶点构成一个极小连通子图,称该极小连通子图为此连通图的生成树。生成树是一种特殊的生成子图。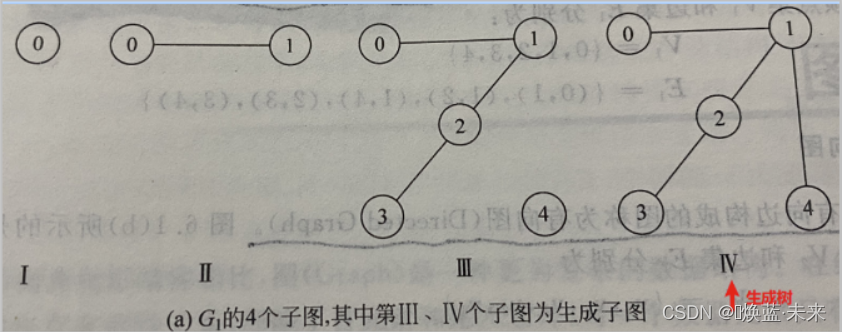
-
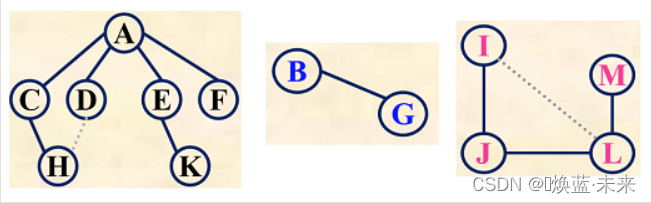
生成森林:对非连通图,则称由各个连通分量的生成树的集合,称为此非连通图的生成森林。

-
三个联通分量的生成树,构成了生成森林
-
1.2 图的抽象数据类型
public interface IGraph {void createGraph(); //创建一个图int getVexNum(); //返回图中的顶点数(vertex)int getArcNum(); //返回图中的边数(arc弧数)Object getVex(int v); //给定顶点的位置,返回对应的顶点值int locateVex(Object vex); //给定定制的值,返回在图中的位置,如果不在图中返回-1int firstAdjVex(int v); //返回v的第一个邻接点,如果没有邻接点返回-1 int nextAdjVex(int v, int w);//返回v相对于w的下一个邻接点,若w是v的最后一个邻接点返回-1// (Adjacent vertex) 相邻顶点
}
1.3 图的存储结构
1.3.1 图的类型&存储结构
-
图的类型主要有4种:无向图、有向图、无向网和有向网。可以用枚举表示:
public enum GraphKind{UDG, //无向图(UnDirected Graph)DG, //有向图(Directed Graph)UDN, //无向网(UnDirected Network)DN, //有向网(Directed Network) } -
图有多种存储结构,每种存储结构都能表示上面的4种的类型。
-
图的存储结构除了存储图中各个顶点的信息外,还需要存储与顶点相关的边的信息。
-
常见图的存储结构:
- 邻接矩阵
- 邻接表
- 邻接多重表
- 十字链表
1.3.2 邻接矩阵:定义
-
图的邻接矩阵:用来表示顶点之间相邻关系的矩阵。
- 图G=(V, E)具有n(n >= 1)个顶点,顶点的顺序依次为{v0,v1,…,vn-1}
- 则图G的邻接矩阵A是一个n阶方阵,定义如下:
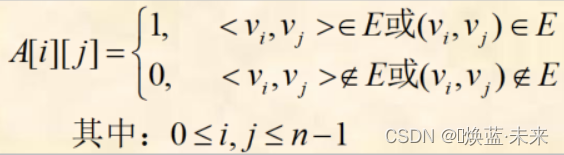
-
无向图的邻接矩阵是对称的,一般可以采用压缩存储。
- 顶点vi的度是第i行或第i列中非零元素的个数。
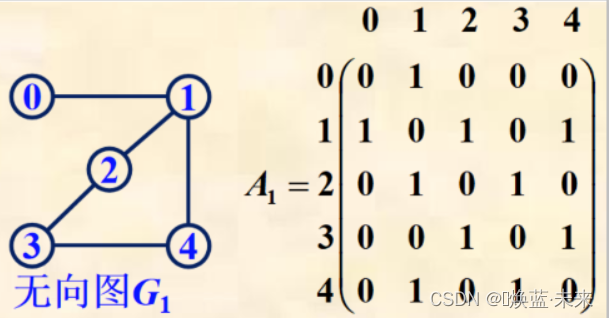
-
有向图的邻接矩阵不一定为对称矩阵。
- 每一行中非零个数为该顶点的出度。
- 每一列中非零个数为该顶点的入度。
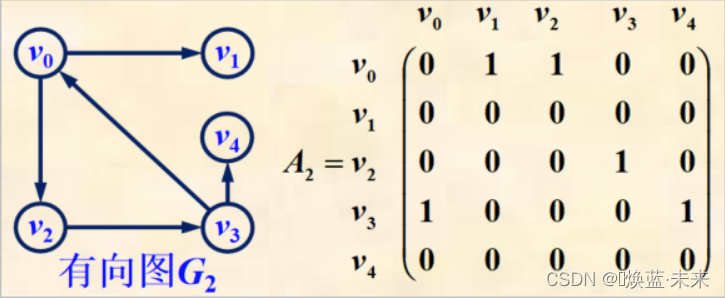
-
网的邻接矩阵的定义:
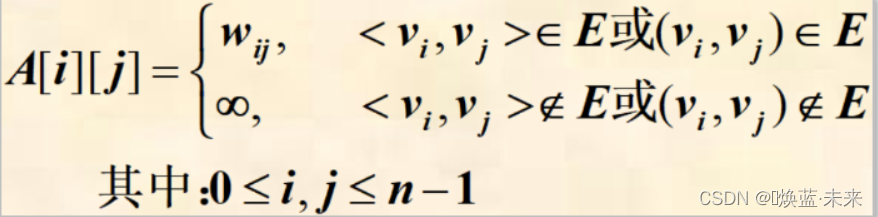
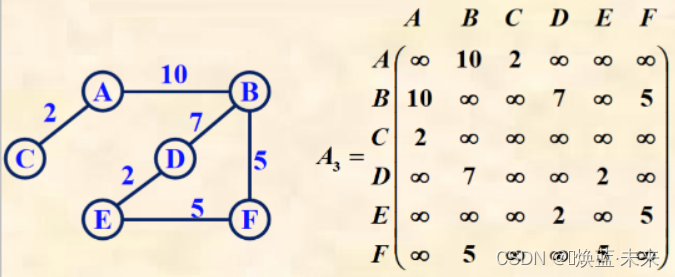
- 练习:有向图的邻接矩阵
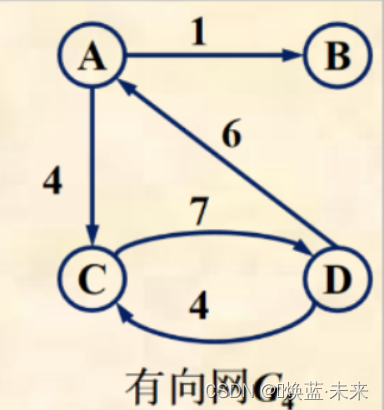

1.3.3 邻接矩阵:类的描述
public class MGraph implements IGraph {public final static int INFINITY = Integer.MAX_VALUE;private GraphKind kind; //图的种类标志private int vexNum, arcNum; //图的当前顶点数和边数private Object[] vexs; //顶点集private int[][] arcs; //邻接矩阵(边集)public void createGraph(){} //创建图private void createUDG() {} //创建无向图private void createDG() {} //创建有向图private void createUDN() {} //创建无向网private void createDN() {} //创建有向网public int getVexNum() { //返回定点数return vexNum;}public int getArcNum() { //返回边数return arcNum;}// 给定顶点的值vex,返回其在图中的位置,如果图中不包含此顶点,则返回-1public int locateVex(Object vex) {}// 返回v表示结点的值,0 <= v <= vexNumpublic Object getVex(int v) throws Exception {}// 返回v的第一个邻接点,若v没有邻接点则返回-1。其中 0 <= v <= vexNumpublic int firstAdjVex(int v) throws Exception {}// 返回v相对于w的下一个邻接点,若w是v的最后一个邻接点,则返回-1。其中 0 <= v,w <= vexNumpublic int nextAdjVex(int v, int w) throws Exception {}
}
1.3.4 邻接矩阵:基本操作
1)创建图
// 创建图public void createGraph() {// 获得用户输入的图的类型Scanner sc = new Scanner(System.in);System.out.println("请输入图的类型:");GraphKind kind = GraphKind.valueOf(sc.next()); //通过字符串获得对应枚举类型switch (kind) { //根据不同的枚举值,选择不同的图或网的创建case UDG:createUDG(); // 构建无向图return;case DG:createDG(); // 构建有向图return;case UDN:createUDN(); // 构建无向网return;case DN:createDN(); // 构建有向网return;}}
2)创建无向网
-
输入图的顶点、边及权值构造无向图,步骤:
- 输入顶点数或边数
- 根据图的顶点数构建邻接矩阵
- 根据图的边数,确定输入边的数目
- 根据输入每条边的顶点再邻接矩阵相应位置保存每条边的权值。
-
代码
private void createUDN() {//初始化变量Scanner sc = new Scanner(System.in);System.out.println("请分别输入图的顶点数、图的边数:");vexNum = sc.nextInt();//顶点数narcNum = sc.nextInt();//边数e//输入图中各顶点vexs = new Object[vexNum]; //顶点集对应的数组System.out.println("请分别输入图的各个顶点:");for (int v = 0; v < vexNum; v++) //通过循环依次输入各个顶点vexs[v] = sc.next();//定义邻接矩阵arcs = new int[vexNum][vexNum];// 初始化邻接矩阵for (int v = 0; v < vexNum; v++)for (int u = 0; u < vexNum; u++)arcs[v][u] = INFINITY; //初始为无穷大//输入边信息System.out.println("请输入各个边的两个顶点及其权值:");for (int k = 0; k < arcNum; k++) {int v = locateVex(sc.next()); //顶点int u = locateVex(sc.next()); //顶点arcs[v][u] = arcs[u][v] = sc.nextInt(); //权值, 对称}
}
初始化变量: O ( 1 ) 输入图中各顶点: O ( n ) 定义邻接矩阵: O ( n 2 ) 输入边信息: O ( e × n ) 总的时间复杂度: O ( n 2 + n + e × n + 1 ) = O ( n 2 + e n ) 初始化变量:O(1) \\ 输入图中各顶点:O(n) \\ 定义邻接矩阵:O(n^2) \\ 输入边信息:O(e×n) \\ 总的时间复杂度:O(n^2+n+e×n+1) = O(n^2+en) 初始化变量:O(1)输入图中各顶点:O(n)定义邻接矩阵:O(n2)输入边信息:O(e×n)总的时间复杂度:O(n2+n+e×n+1)=O(n2+en)
3)创建有向网
// 构建有向网private void createDN() {Scanner sc = new Scanner(System.in);System.out.println("请分别输入图的顶点数、图的边数:");vexNum = sc.nextInt();arcNum = sc.nextInt();vexs = new Object[vexNum];System.out.println("请分别输入图的各个顶点:");for (int v = 0; v < vexNum; v++)//构造顶点向量vexs[v] = sc.next();arcs = new int[vexNum][vexNum];for (int v = 0; v < vexNum; v++)// 初始化邻接矩阵for (int u = 0; u < vexNum; u++)arcs[v][u] = INFINITY;System.out.println("请输入各个边的两个顶点及其权值:");for (int k = 0; k < arcNum; k++) {int v = locateVex(sc.next());int u = locateVex(sc.next());arcs[v][u] = sc.nextInt(); //仅设置顶点v-->顶点u,不是对称的,只需要设置一个}}
4)顶点定位
-
根据顶点信息vex,取得其在顶点数组中的位置,若图中无此顶点,则返回-1。
-
代码
// 根据顶点信息vex,取得其在顶点数组中的位置,若图中无此顶点,则返回-1。public int locateVex(Object vex) {// 遍历顶点数组for (int v = 0; v < vexNum; v++)if (vexs[v].equals(vex))return v;return -1;} -
时间复杂度:O(n)
5)查询第一个邻接点
-
步骤:
- 判断v的合法性
- 顶点v的索引号,对应邻接矩阵的第v行,遍历第v行,查找是否有非0、非无穷大值的元素
-
代码
// 已知图中的一个顶点v,返回v的第一个邻接点,如果v没有连接点,则返回-1,其中0 <= v < vexNum public int firstAdjVex(int v) throws Exception {if (v < 0 || v >= vexNum)throw new Exception("第" + v + "个顶点不存在!");for (int j = 0; j < vexNum; j++)if (arcs[v][j] != 0 && arcs[v][j] < INFINITY)return j;return -1; } -
时间复杂度:O(n)
6)查找下一个邻接点
-
步骤:
- 判断v的合法性
- 从邻接矩阵第v行第w+1列开始遍历查找是否有非0、非无穷大值的元素
-
代码
public int nextAdjVex(int v, int w) throws Exception {if (v < 0 || v >= vexNum)throw new Exception("第" + v + "个顶点不存在!");for (int j = w + 1; j < vexNum; j++)if (arcs[v][j] != 0 && arcs[v][j] < INFINITY)return j;return -1; } -
时间复杂度:O(n)
1.3.5 邻接表:定义
-
邻接表是图的一种链式存储方法
-
邻接表由一个顺序存储的顶点表和n个链式存储的边表组成。
-
顶点表由顶点结点组成
-
边表:
- 无向图:由边结点组成的一个单链表,表示所有依附于顶点vi的边。
- 有向图:由弧结点组成的一个单链表,表示所有以顶点vi为始点的弧。
-
链式存储结点:
-
图结点由2部分组成:第一个邻接点、下一个邻接点
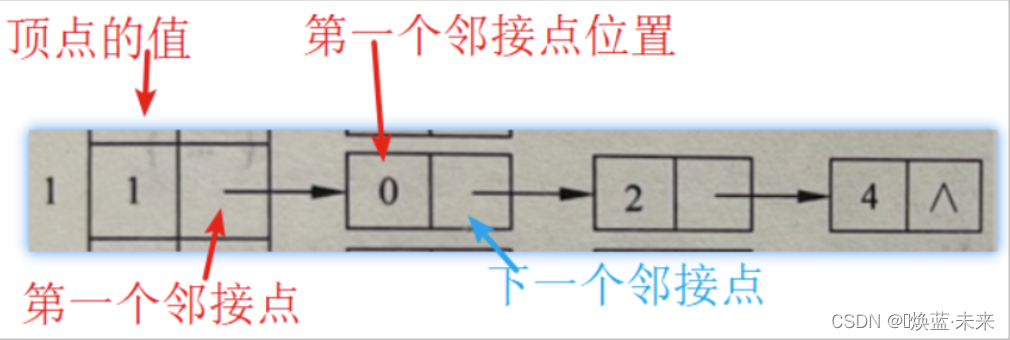
-
网结点有3部分组成:第一个邻接点、权值、下一个邻接点
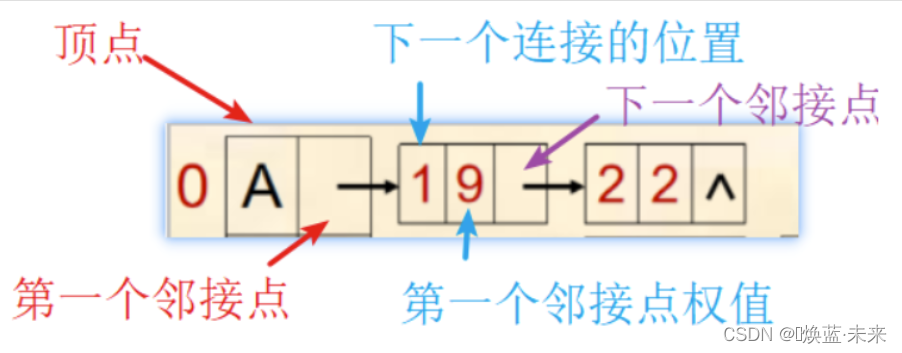
-
-
-
无向图:对应的邻接表某行上边结点个数为该行表示结点的度。
- 如果无向图(网)中有e条边,则对应邻接表有2e个边结点。
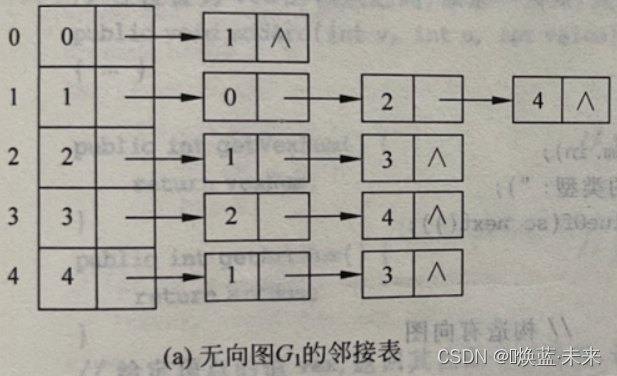
- 无向网邻接表
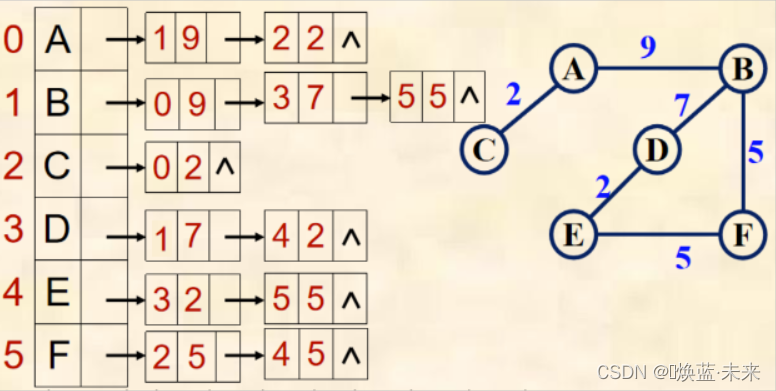
-
有向图:
- 邻接表:边表表示所有以vi为始点的弧。
- 对应的邻接表某行上边结点个数为该结点的出度。
- 在有向图的邻接表中不易找到指向该顶点的弧。
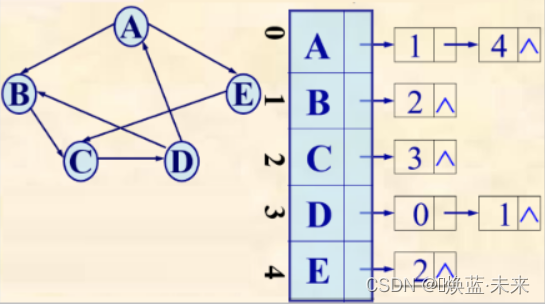
-
逆邻接表:边表表示所有以vi为终点的弧。
- 对应的逆邻接表某行上边结点个数为该结点的入度。
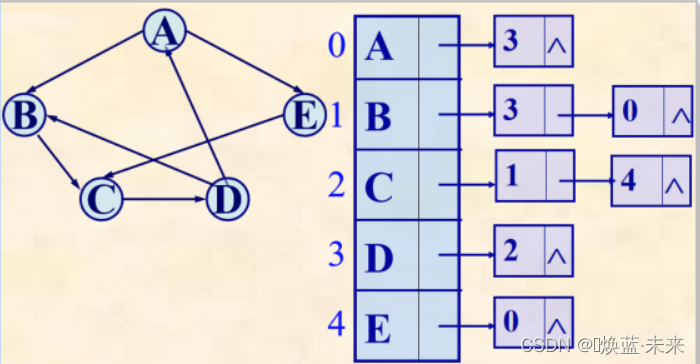
-
如果有向图(网)中有e条边,则对应邻接表有e个边结点。

- 邻接表:边表表示所有以vi为始点的弧。
-
邻接表与邻接矩阵对比:
- 对于稀疏图,邻接表比邻接矩阵节省存储空间
- 邻接表上很容易找到任意一个顶点,的邻接点和,但若要判定任意两个邻接点是否有边相连,则需遍历单链表,不如邻接矩阵方便。
1.3.6 邻接表:相关类
-
顶点结点类

//图的邻接表存储表示中的顶点结点类 public class VNode {public Object data; //顶点信息public ArcNode firstArc; //指向第一个依附于该顶点的弧 } -
边(弧)结点类

//图的邻接表存储表示中的边(弧)结点类 public class ArcNode {public int adjVex; //该弧所指向的顶点位置public int value; //边(或弧)的权值public ArcNode nextArc; //指向下一条弧 } -
邻接表类
//创建邻接表 public class ALGraph implements IGraph {private GraphKind kind; //图的种类标志private int vexNum, arcNum; //图的当前顶点数和边数private VNode[] vexs; //顶点private void createUDN() { //创建无向网}private void createDN() { //创建有向网}// 给定顶点的值vex,返回其在图中的位置,若图中不包含该顶点的,则返回-1public int locateVex(Object vex) {}// 在图中插入边结点public void addArc(int v, int u, int value) {}// 返回v的第一个邻接点,若v没有邻接点则返回-1。其中 0 <= v <= vexNumpublic int firstAdjVex(int v) throws Exception {}// 返回v相对于w的下一个邻接点,若w是v的最后一个邻接点,则返回-1。其中 0 <= v,w <= vexNumpublic int nextAdjVex(int v, int w) throws Exception {} }
1.3.6 邻接表:基本操作
1)创建无向网
- 步骤:
- 输入顶点数和边数
- 构建顶点向量
- 根据图的边数,确定输入边的数目
- 根据输入的每条边生成结点,并在相应位置插入边结点
- 代码
// 无向网的创建算法
private void createUDN() {//初始化变量Scanner sc = new Scanner(System.in);System.out.println("请分别输入图的顶点数、图的边数:");vexNum = sc.nextInt(); //顶点数narcNum = sc.nextInt(); //边数e//输入图中各顶点vexs = new VNode[vexNum];System.out.println("请分别输入图的各顶点:");// 构造顶点向量for (int v = 0; v < vexNum; v++)vexs[v] = new VNode(sc.next());//输入图中各边信息System.out.println("请输入各边的顶点及其权值:");for (int k = 0; k < arcNum; k++) {int v = locateVex(sc.next()); // 弧尾int u = locateVex(sc.next()); // 弧头int value = sc.nextInt(); // 权值addArc(v, u, value); //加入边addArc(u, v, value); //加入边}
}
2)创建有向网
// 创建有向网private void createDN() {Scanner sc = new Scanner(System.in);System.out.println("请分别输入图的顶点数、图的边数:");vexNum = sc.nextInt();arcNum = sc.nextInt();vexs = new VNode[vexNum];System.out.println("请分别输入图的各顶点:");for (int v = 0; v < vexNum; v++)// 构建顶点向量vexs[v] = new VNode(sc.next());System.out.println("请输入各边的顶点及其权值:");for (int k = 0; k < arcNum; k++) {int v = locateVex(sc.next());// 弧尾int u = locateVex(sc.next());// 弧头int value = sc.nextInt();addArc(v, u, value); // 一个方向}}
3)顶点定位
// 给定顶点的值vex,返回其在图中的位置,若图中不包含该顶点的,则返回-1public int locateVex(Object vex) {for (int v = 0; v < vexNum; v++)if (vexs[v].data.equals(vex))return v;return -1;}
4)插入边
-
核心思想:往链式存储的边表头插入一个新结点
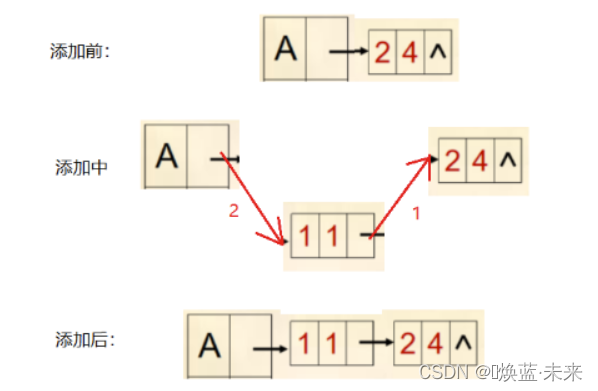
// 在图中插入边结点public void addArc(int v, int u, int value) {ArcNode arc = new ArcNode(u, value); //u为边的终点,生成边结点arc.nextArc=vexs[v].firstArc; //v为边的起点,将边结点插入顶点v 的链表表头vexs[v].firstArc=arc; //生成新表头}
5)第一个邻接点

// 已知图中的一个顶点v,返回v的第一个邻接点,如果v没有连接点,则返回-1,其中0 <= v < vexNumpublic int firstAdjVex(int v) throws Exception {if (v < 0 || v >= vexNum)throw new Exception("第" + v + "个顶点不存在!");VNode vex = vexs[v];if (vex.firstArc != null)return vex.firstArc.adjVex;elsereturn -1;}
6)查询下一个邻接点
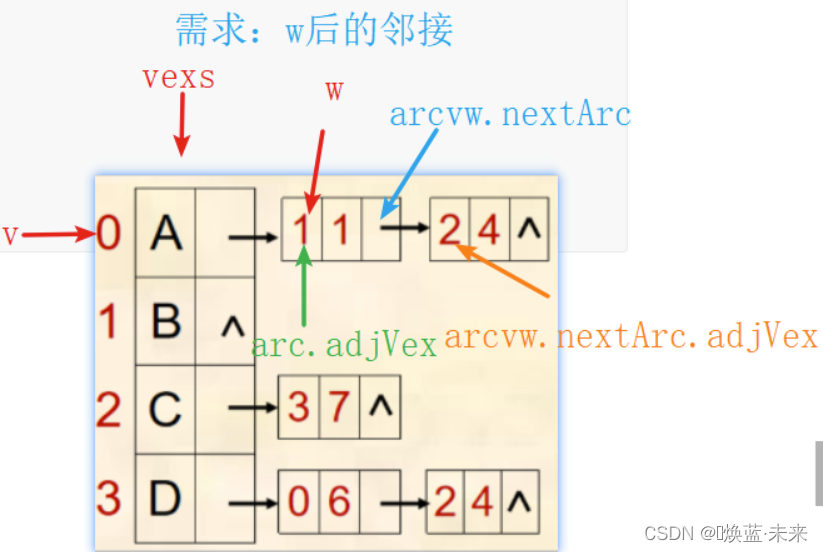
public int nextAdjVex(int v, int w) throws Exception {if (v < 0 || v >= vexNum)throw new Exception("第" + v + "个顶点不存在!");VNode vex = vexs[v];ArcNode arcvw = null;// 获得w结点在链表中所在的位置for (ArcNode arc = vex.firstArc; arc != null; arc = arc.nextArc)if (arc.adjVex == w) {arcvw = arc;break;}// 返回w的下一个邻接点if (arcvw != null && arcvw.nextArc != null)return arcvw.nextArc.adjVex;elsereturn -1;}
1.3.7 练习
- 给出下图的邻接表和邻接矩阵
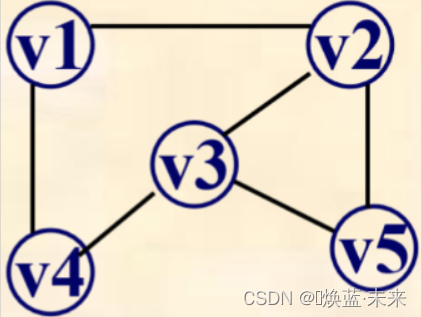
-
邻接矩阵
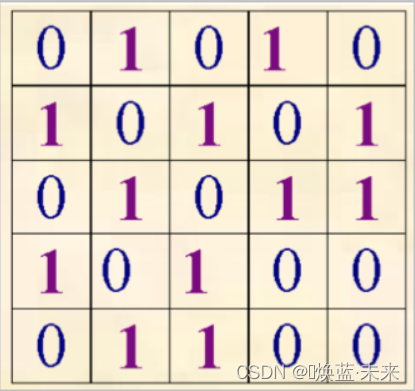
-
邻接表
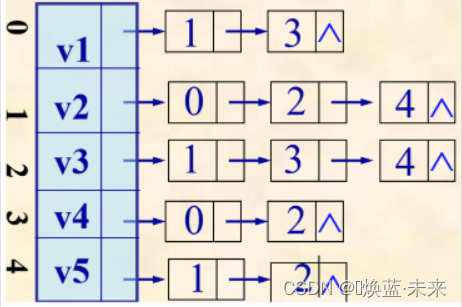
1.4 图的遍历
- 图的遍历:指从图中的某个顶点出发,对图中的所有顶点访问且仅访问一次的过程。
- 常见的遍历方式:
- 广度优先搜索 BFS (Breadth First Search),类似于树的层次遍历,是树的层次遍历的推广。
- 深度优先搜索 DFS (Depth First Search),类似于树的先根遍历,是树的先根遍历的推广。
1.4.1 广度优先搜索
1)定义
-
从图中的某个顶点v开始,先访问该顶点再依次访问该顶点的每一个未被访问过的邻接点 w1、w2、…
-
然后按此顺序访问顶点w1、w2、…的各个还未被访问过的邻接点。
-
重复上述过程,直到图中的所有顶点都被访问过为止。
-
实例:
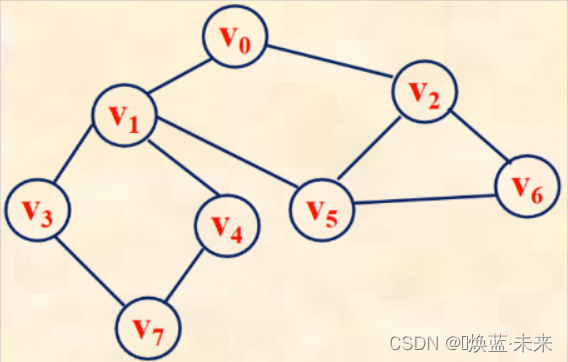
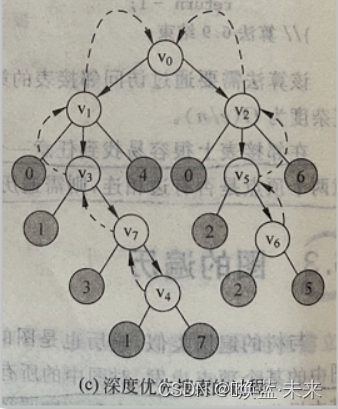
访问次序:v0、v1、v2、v3、v4、v5、v6、v7
-
对于一个图,从某个顶点出发可得到
多种搜索遍历结果,即一个图的BFS序列不唯一。 -
但给定
起始点及图的存储结构时,BFS算法所给出的BFS序列是唯一的。 -
练习:
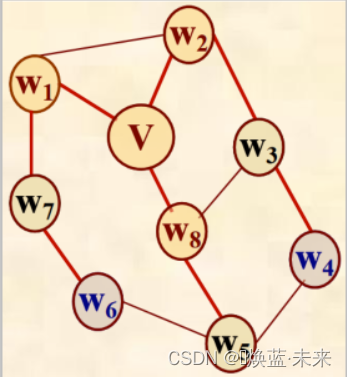
访问次序:v、w1、w2、w8、w7、w3、w5、w6、w4
2)算法分析
- 核心思想:使用队列记录所有的结点,只要进入到队伍,表示被访问。

- 总结:广度优先搜索遍历中,需要使用队列,依次记住被访问过的顶点,因此,算法开始时,访问起始点V,并将其插入队列中,以后每次从队列中删除一个数据元素,就依次访问它的每一个未被访问过的邻接点,并将其插入队列中。这样当队列为空的时候,表明所有与起始点相通的顶点都已被访问完毕,算法结束。
- 顶点的出队顺序,就是广度优先搜索遍历的序列。
3)算法实现
- 算法核心:
- 使用一个队列记录当前节点,所有未被访问的邻接点。
- 使用一个visited数组,记录顶点是否被访问
public class BTraverser {private static boolean[] visited;// 访问标志数组// 对图G做广度优先遍历public static void BFSTraverse(IGraph G) throws Exception {visited = new boolean[G.getVexNum()];// 访问标志数组for (int v = 0; v < G.getVexNum(); v++)// 访问标志数组初始化visited[v] = false;for (int v = 0; v < G.getVexNum(); v++)if (!visited[v]) // v尚未访问BFS(G, v);}private static void BFS(IGraph G, int v) throws Exception {visited[v] = true;System.out.print(G.getVex(v).toString() + " ");LinkQueue Q = new LinkQueue();// 辅助队列QQ.offer(v);// v入队列while (!Q.isEmpty()) {int u = (Integer) Q.poll();// 队头元素出队列并赋值给ufor (int w = G.firstAdjVex(u); w >= 0; w = G.nextAdjVex(u, w))if (!visited[w]) {// w为u的尚未访问的邻接顶点visited[w] = true;System.out.print(G.getVex(w).toString() + " ");Q.offer(w);}}}public static void main(String[] args) throws Exception {ALGraph G = GenerateGraph.generateALGraph();BTraverser.BFSTraverse(G);}
}
4)性能分析
- 广度优先搜索遍历图的过程,实际上就是寻找队列中顶点的邻接点的过程。
- 假设图中有n个顶点和e条边
- 时间复杂度
- 当图的存储结构采用
邻接矩阵时,需要扫描邻接矩阵的每一个顶点,其时间复杂度为O(n2) - 当图的存储结构采用
邻接表时,需要扫描邻接表中的每一个单链表,其时间复杂度为O(e)
- 当图的存储结构采用
- 空间复杂度
- 需要使用队列,依次记住被访问过的顶点,每一个顶点最多入队、出队一次,空间复杂度为O(n)
- 增设一个辅助数组visited,空间复杂度为O(n)。
- 时间复杂度
1.4.2 深度优先搜索
1)定义
- 连通图的深度优先搜索遍历
- 从图中某个顶点v0出发,访问此顶点,然后依次从v0的各个未被访问的邻接点出发深度优先搜索遍历图,直到图中所有和v0有路径想通的顶点都被访问到。
- 非连通图处理方法:
- 访问完一个连通分量后,再在图中选一个未曾被访问的顶点作为始点继续进行深度优先搜索遍历。
2)算法分析
-
一个图的DFS序列不是唯一的,但给定
起始点及图的存储结构时,DFS算法所给出的序列是唯一的。 -
练习:从顶点v0开始遍历
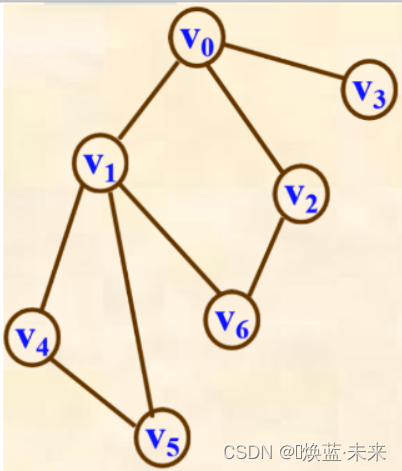
序列1:v0、v1、v4、v5、v6、v2、v3
序列2:v0、v2、v6、v1、v5、v4、v3

3)算法实现
- 算法核心:递归
public class DTraverser {private static boolean[] visited;// 访问标志数组// 对图G做深度优先遍历public static void DFSTraverse(IGraph G) throws Exception {visited = new boolean[G.getVexNum()];for (int v = 0; v < G.getVexNum(); v++)// 访问标志数组初始化visited[v] = false;for (int v = 0; v < G.getVexNum(); v++)if (!visited[v])// 对尚未访问的顶点调用DFSDFS(G, v);}// 从第v个顶点出发递归地深度优先遍历图Gpublic static void DFS(IGraph G, int v) throws Exception {visited[v] = true;System.out.print(G.getVex(v).toString() + " ");// 访问第v个顶点//对顶点v的每一个未被访问的邻接点进行DFS操作for (int w = G.firstAdjVex(v); w >= 0; w = G.nextAdjVex(v, w))if (!visited[w])// 对v的尚未访问的邻接顶点w递归调用DFSDFS(G, w);}public static void main(String[] args) throws Exception {ALGraph G = GenerateGraph.generateALGraph();DTraverser.DFSTraverse(G);}
}
4)性能分析
- 深度优先搜索遍历图的时间复杂度和广度优先遍历相同,不同之处仅在于对顶点的访问顺序不同。
- 图的存储结构采用
邻接矩阵时,时间复杂度为O(n2)。 - 图的存储结构采用
邻接表时,时间复杂度为O(e)。
1.4.3 练习
1)例1
已知一个图,若从顶点v1出发,分别写出一种按深度优先搜索和广度优先搜索进行遍历的遍历序列。
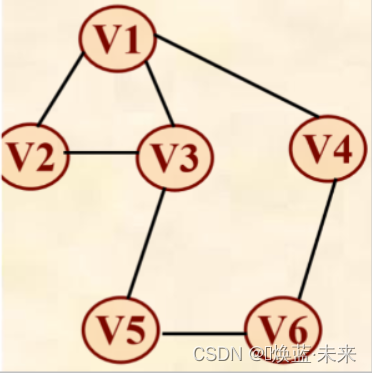
深度优先搜索遍历序列:V1、V2、V3、V5、V6、V4
广度优先搜索遍历序列:V1、V2、V3、V4、V5、V6
2)例2
已知一个图的邻接表存储结构,如下图,若从顶点v1出发,分别写出有向图按深度优先搜索法进行遍历和按广度优先搜索法进行遍历得到的顶点序列
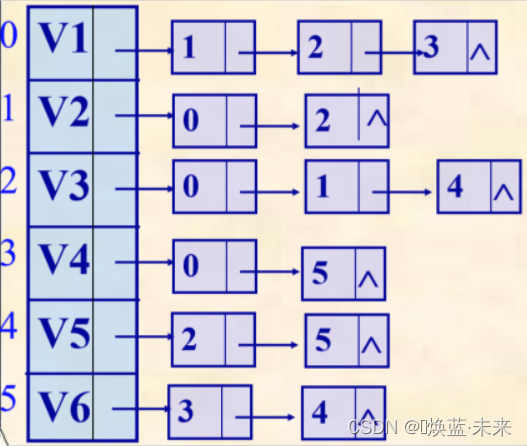

深度优先搜索法遍历序列:V1、V2、V3、V5、V6、V4
广度优先搜索法遍历序列:V1、V2、V3、V4、V5、V6
1.5 最小生成树
1.5.1 基本概念
1)树的特性
-
连通图的生成树(Spanning Tree)
-
是图的极小连通子树,它包含图中的全部顶点,但只有构成一颗树的边
(极小连通子树:边是最少的,不能在少,否则不连通)
-
生成树又是图的极大无回路子图,它的边集是关联图中的所有顶点而又没有形成回路的边。
(极大无回路子图:边不能在多,再多,就回路)
-
一个有n个顶点的连通图的生成树只能有n-1条边。
- 若有n个顶点而少于n-1条边,则是非连通图。
- 若多余n-1条边,则一定形成回路。
- 有n-1条边的生成子图并不一定是生成树。
-
图的生成树不是唯一的。
-
-
连通图生成树,根据遍历方式分为:
- 由广度优先遍历得到的生成树,称为广度优先生成树。
- 由深度优先遍历得到的生成树,称为深度优先生成树。

-
非连通图的生成森林
- 对于非连通图,每一个连通分量中的顶点集和遍历时经过的边一起构成若干棵生成树,这些生成树组成了该非连通图的生成森林。
-
非连通图生成森林,根据遍历方式分为:
- 由广度优先遍历得到的生成森林,称为广度优先生成森林。
- 由深度优先遍历得到的生成森林,称为深度优先生成森林。
2)最小生成树
-
问题:
假设要在n个城市之间建立通讯联络网,则连通n个城市只需要修建n-1条线路,如何在最节省经费的前提下建立这个通讯网?
-
等效问题:
构建网的一颗最小生成树,即:在e条带权的边中选取n-1条边(不构成回路),使权值之和为最小?
-
最小生成树:
- 在一个网的所有生成树中,权值总和最小的生成树称为最小代价生成树,也称为最小生成树。
-
构建最小生成树的准则:
- 只能使用该图中的边构造最小生成树
- 当且仅当使用n-1条边来连接图中的n个顶点
- 不能使用产生回来的边。
-
求图的最小生成树的典型算法:
- 克鲁斯卡尔(Kruskal)算法
- 普里姆(Prim)算法
(考虑问题的出发点相同:为使生成树上边的权值之和达到最小,则应使生成树中每一条边的权值尽可能的小)
1.5.2 克鲁斯卡尔(Kruskal)算法
1)概述
- 先构造一个只含n个顶点的子图SG,然后从权值最小的边开始,若它的添加不使SG中产生回路,则在SG上加上这条边,如此重复,直至加上n-1条边为止。
2)算法分析
- 设图G=(V, E) 是一个具有n个顶点的连通无向图,T=(V, TE)是图G的最小生成树。
- V是T的顶点集
- TE是T的边集
- 构建最小生成树的步骤:
- T的初始化状态 T = (V, 空 ) ,即最小生成树T是图G的生成零图。
- 将图G中的边按照权值从小到大的顺序排序
- 依次选取每条边,若选取的边未使生成树T形成回路,则加入TE中,否则舍弃。直至TE中包含n-1条边为止
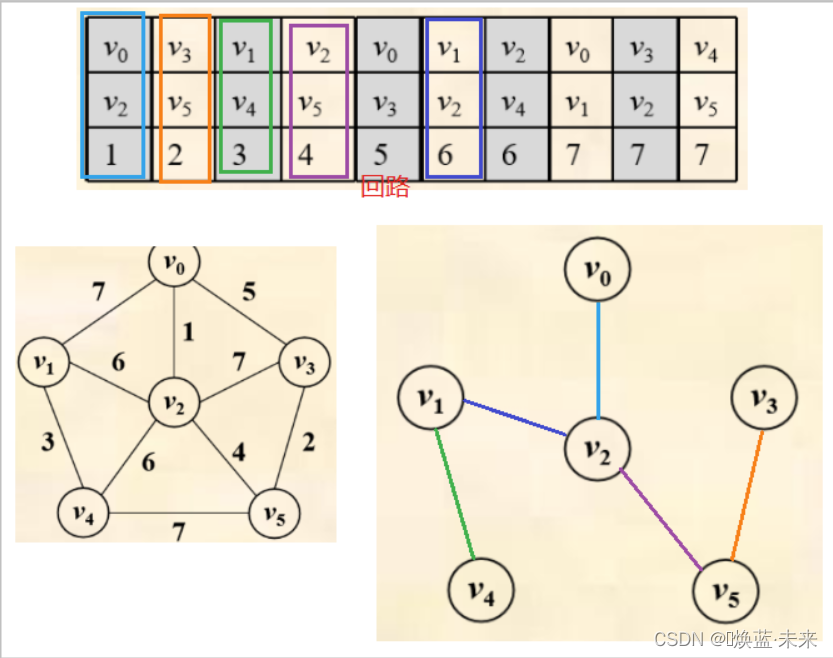
-
PPT动画演示
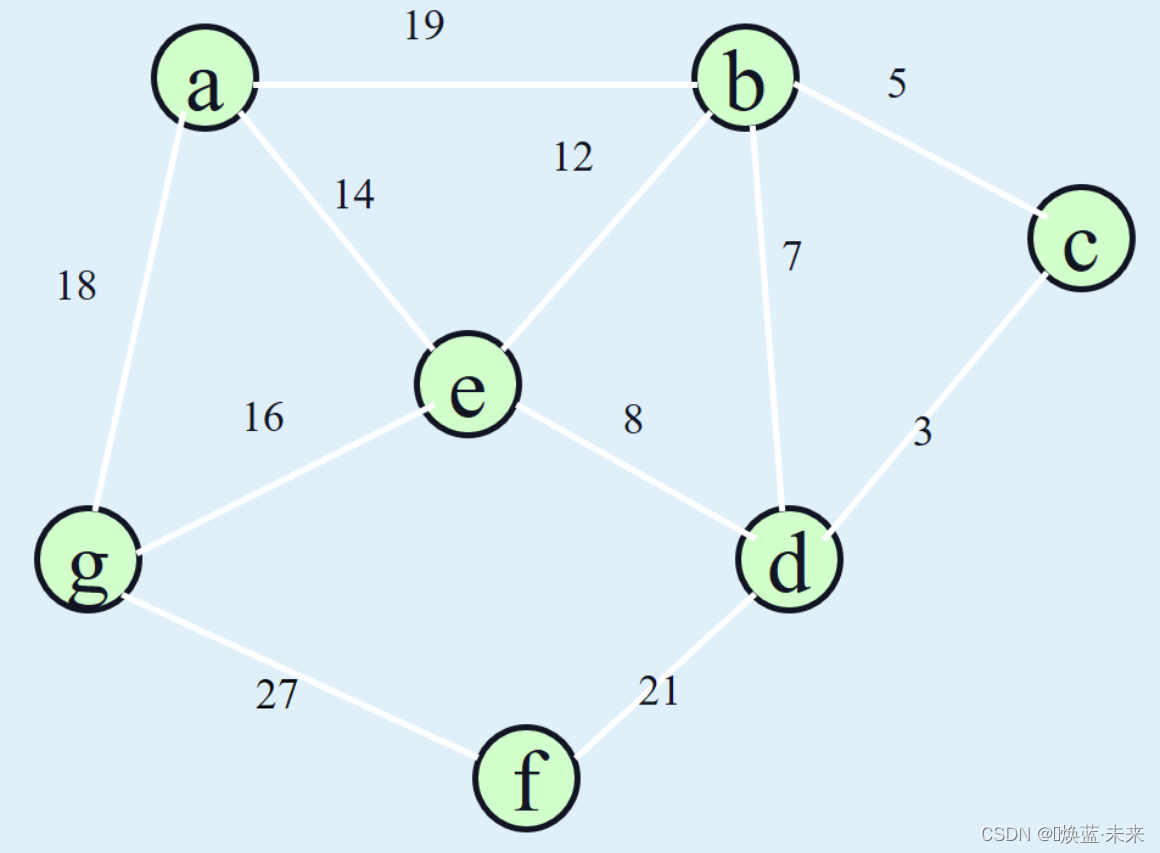

3)性能分析
- 构建最小生成树时,尽可能选择权值最小的边,但并不是每一条权值最小的边都必然可选,有可能构成回路。
- 最小生成树不是唯一的,因为同一时候可能有多重选择。
- 算法的时间复杂度:O(elge) ,即克鲁斯卡尔算法的执行时间主要取决于图的边数。
- 该算法适用于针对稀疏图的操作。
1.5.3 普里姆(Prim)算法
1)概述
- 取图中任意一个顶点v作为生成树的根,之后往生成树上添加新的顶点w。
- 在添加顶点w和已经在生成树上的顶点v之间必定存在一条边,并且该边的权值在所有连通顶点v和w之间的边中取值最小。
- 之后继续往生成树上添加顶点,直至生成树上含有n-1个顶点为止。
2)算法分析
-
PPT演示
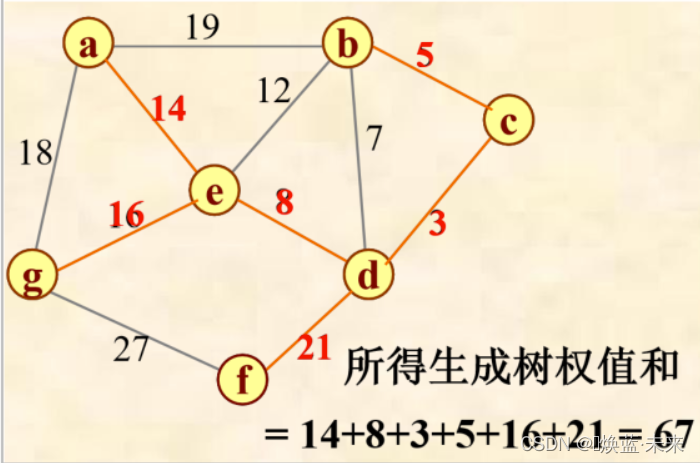
-
补充概念
-
两个顶点之间的距离:指将顶点邻接到的关联边的权值
记为:|u,v|
-
顶点到顶点集合之间的距离:指顶点到顶点集合中所有顶点之间的距离中的最小值。
记为:|u, V| = min |u,v|
-
两个顶点集合之间的距离:指顶点集合到顶点集合中所有顶点之间的距离中的最小值。
记为:|U, V| = min |u, V|
-

3)步骤分析
-
在生成树的构造过程中,图中n个顶点分属两个集合:
已落在生成树上的顶点集合U和尚未落在生成树上的顶级集合V-U,则应在所有连通U中顶点和V-U中的顶点的边中选取权值最小的边。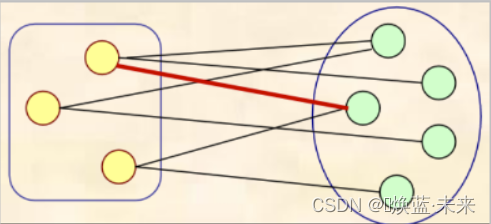
-
设图G=(V, E) 是一个具有n个顶点的连通无向图,T=(V, TE) 是图G的最小生成树。
- 从V中任意取一顶点,将它并入U中,
- 每次选择U内顶点到V-U所有边中最小的,
- 并将另一个不在U内的顶点并入U,相应的边并入TE中,
- 直到所有顶点都并入U中。
-
PPT动画演示
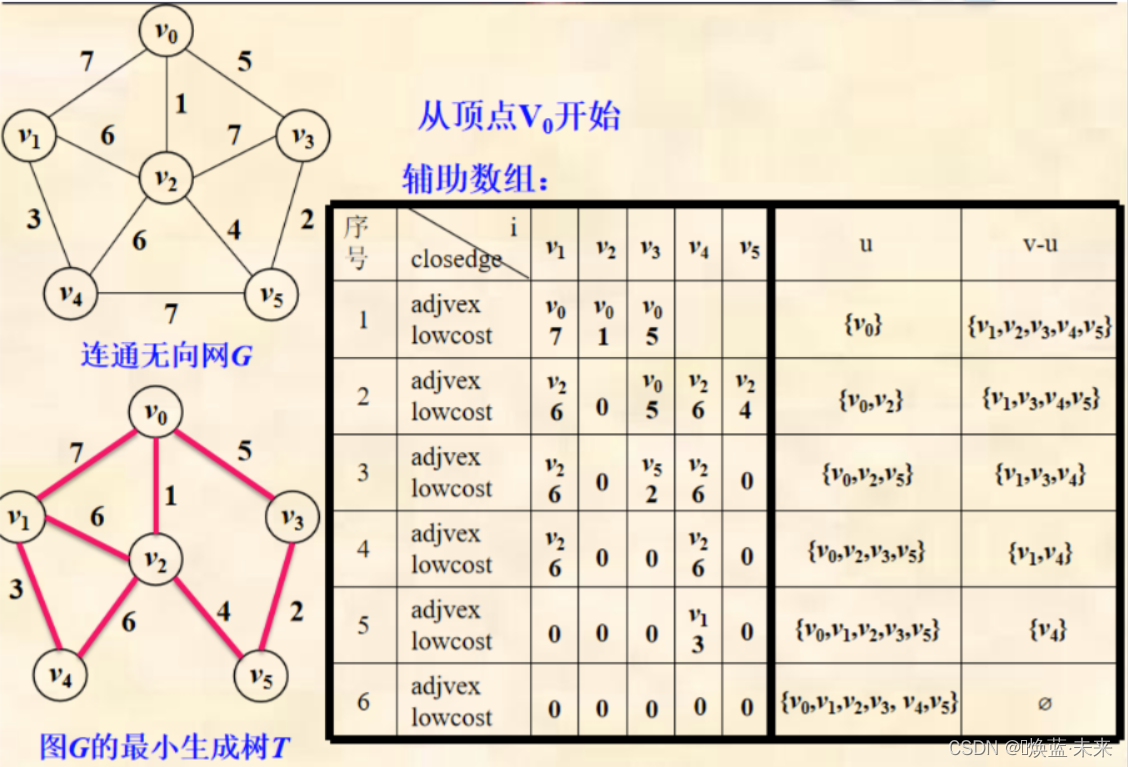
4)代码实现
-
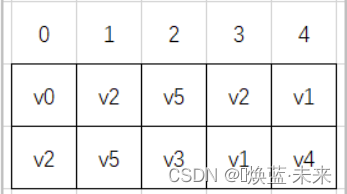
程序最后运行结果
-
辅助数组
-
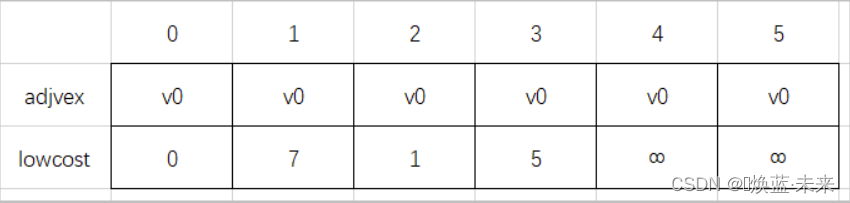
初始化数据
-
第一轮处理(v0与v1连通)
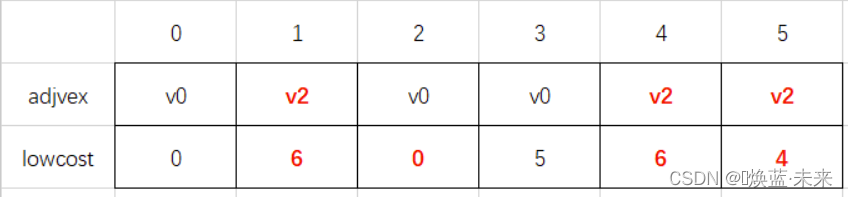
-
-
算法
public class MiniSpanTree_PRIM {// 内部类辅助记录从顶点U到V-U的代价最小的边private class CloseEdge {Object adjVex;int lowCost;public CloseEdge(Object adjVex, int lowCost) {this.adjVex = adjVex; //顶点this.lowCost = lowCost; //两个顶点之间最下的权值,}}// 用普里姆算法从第u个顶点出发构造网G的最小生成树T,返回由生成树边组成的二维数组public Object[][] PRIM(MGraph G, Object u) throws Exception {// 用于记录最小生成树的顶点,例如:tree[0][0]="v0",tree[0][1]="v2"Object[][] tree = new Object[G.getVexNum() - 1][2];int count = 0; // 初始化数据CloseEdge[] closeEdge = new CloseEdge[G.getVexNum()];int k = G.locateVex(u); //当前节点在for (int j = 0; j < G.getVexNum(); j++) // 辅助数组初始化if (j != k)closeEdge[j] = new CloseEdge(u, G.getArcs()[k][j]);// 当最小权值为0时,表示当前节点已经在树中closeEdge[k] = new CloseEdge(u, 0); // 初始,U={u}for (int i = 1; i < G.getVexNum(); i++) { // 选择其余G.vexnum - 1个顶点k = getMinMum(closeEdge); // 求出T的下一个结点:第k个顶点tree[count][0] = closeEdge[k].adjVex; // 生成树的边放入数组tree[count][1] = G.getVexs()[k]; //count++;closeEdge[k].lowCost = 0; // 第k个顶点并入U集for (int j = 0; j < G.getVexNum(); j++) //新顶点并入U后重新选择最小边if (G.getArcs()[k][j] < closeEdge[j].lowCost)closeEdge[j] = new CloseEdge(G.getVex(k), G.getArcs()[k][j]);}return tree;}//在closeEdge中选出lowCost最小且不为0的顶点private int getMinMum(CloseEdge[] closeEdge) {int min = Integer.MAX_VALUE;int v = -1;for (int i = 0; i < closeEdge.length; i++)if (closeEdge[i].lowCost != 0 && closeEdge[i].lowCost < min){min = closeEdge[i].lowCost;v = i;}return v;}
}
- 测试类
package book.ch06;public class Example6_4 {public final static int INFINITY = Integer.MAX_VALUE;public static void main(String[] args) throws Exception {Object vexs[] = { "v0", "v1", "v2", "v3", "v4", "v5" };// 各顶点之间边的关系int[][] arcs = { { 0, 7, 1, 5, INFINITY, INFINITY },{ 7, 0, 6, INFINITY, 3, INFINITY }, { 1, 6, 0, 7, 6, 4 },{ 5, INFINITY, 7, 0, INFINITY, 2 },{ INFINITY, 3, 6, INFINITY, 0, 7 },{ INFINITY, INFINITY, 4, 2, 7, 0 } };MGraph G = new MGraph(GraphKind.UDG, 6, 10, vexs, arcs);Object[][] T = new MiniSpanTree_PRIM().PRIM(G, "v1");for (int i = 0; i < T.length; i++)System.out.println(T[i][0] + " - " + T[i][1]);}
}
// 开始顶点v1 调试结果:
// v1 - v4
// v1 - v2
// v2 - v0
// v2 - v5
// v5 - v3// 开始顶点v0 调试结果:
//v0 - v2
//v2 - v5
//v5 - v3
//v2 - v1
//v1 - v4
5)性能分析
- 普利姆算法的时间复杂度为:O(n2),执行时间主要取决于图的顶点数,与边数无关。
- 该算法适用于稠密图的操作。
1.5.4 两个算法对比
| 算法名 | 普里姆算法 | 克鲁斯卡尔算法 |
|---|---|---|
| 时间复杂度 | O(n2) | O(eloge) |
| 适应范围 | 稠密图 | 稀疏图 |
1.5.5 练习
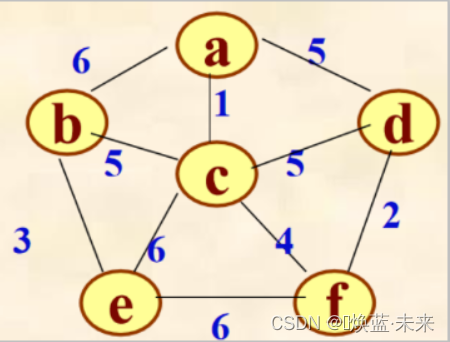
- 分别使用克鲁斯卡尔算法和普利姆算法构建相应的最小生成树
1.6 最短路径
1.6.1 某个顶点到其余各顶点的最短路径
1)概述
- 网经常用于描述一个城市或城市间的交通运输网络。
- 以顶点表示一个城市或某个交通枢纽
- 以边表示两地之间的交通状况
- 边上的权值表示各种相关信息
- 当两个顶点之间存在多条路径时,其中必然存在一条“最短路径”
- 名词:
- 源点(Source):路径中的第一个顶点
- 终点(Destination):最后一个顶点
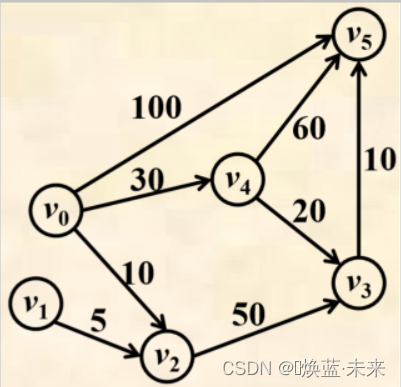
2)实例
-
从源点v0到终点v5存在多条路径
(v0, v5) 的长度为 100
(v0, v4, v5) 的长度为 90
(v0,v4,v3 v5) 的长度为 60 //最短路径
(v0, v2,v3, v5) 的长度为 70
-
从源点v0到各终点的最短路径:
v0到终点v1不存在路径
(v0,v2) 的最短路径长度为10
(v0,v4,v3) 的最短路径长度为50
(v0,v4) 的最短路径长度为30
(v0,v4,v3,v5) 的最短路径长度为60
3)迪杰斯特拉(Dijkstra)算法:概述
- 算法描述:
- 用于求解某个源点到其余各顶点的最短路径。
- 按最短路径长度递增的次序求解
- 类似于普利姆算法
- 每一条最短路径必定只有两种情况:
- 由源点直接到达终点
- 只经过已经求得最短路径的顶点到达终点
- 迪杰斯特拉算法解决的问题:如何实现“按最短路径长度递增的次序”求解
- 解决方法:
- 每次选出当前的一条最短路径
- 算法中需要引入一个辅助向量D,它的每个分类D[i]存放当前所找到的从源点到各个终点vi的最短路径长度。
4)迪杰斯特拉(Dijkstra)算法:算法分析
- 初始若从源点v到各个终点有弧,则存在一条路径,路径长度即为该弧上的权值,保存于D中
- 求得一条到达某个终点的最短路径,即当前路径中的最小值,该顶点即为w
- 检查是否存在经过顶点w的其他路径,若存在,判断其长度是否比当前求得的路径长度短,若是,则修改D中当前最短路径。
- 重复上面的2和3
-
PPT演示
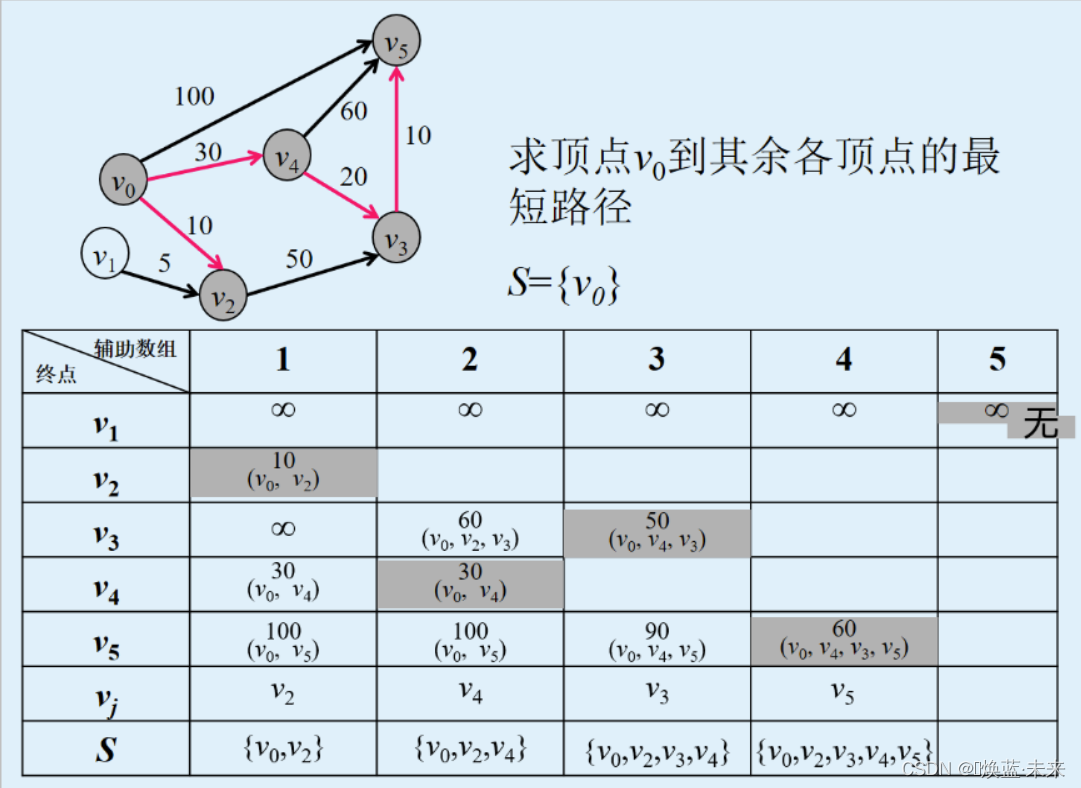
5)迪杰斯特拉(Dijkstra)算法:代码实现
-
测试数据
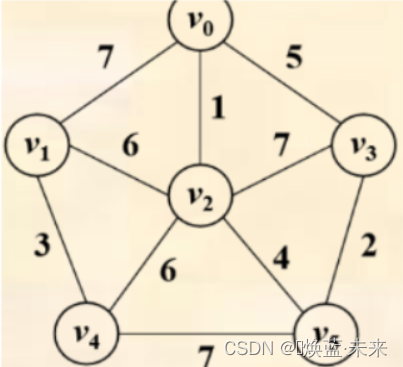
-
处理后的数组P的内容
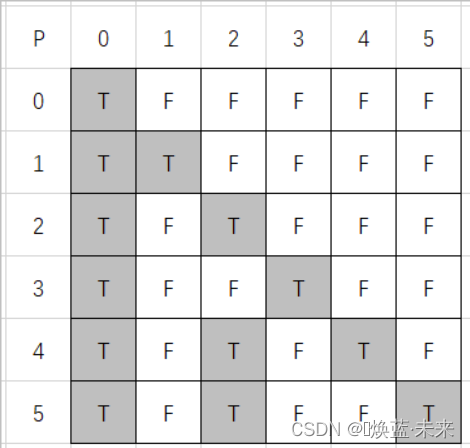
-
处理后数组D的内容
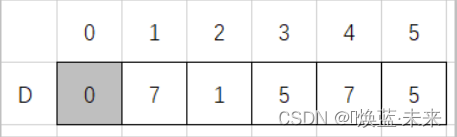
-
算法
package ch06;public class ShortestPath_DIJ {private boolean[][] P;// v0到其余顶点的最短路径, 若P[v][w]为true,则w是从v0到v当前求得最短路径上的顶点private int[] D;// v0到其余顶点的带权长度public final static int INFINITY = Integer.MAX_VALUE;// 用Dijkstra算法求有向网G的v0顶点到其余顶点v的最短路径P[v]及其权值D[v]public void DIJ(MGraph G, int v0) {int vexNum = G.getVexNum();P = new boolean[vexNum][vexNum]; // 用于记录经过的顶点D = new int[vexNum]; // 用于记录到达某顶点需要的最短路径和boolean[] finish = new boolean[vexNum];// finish[v]为true当且仅当v属于S,即已经求得从v0到v的最短路径// 数据初始化for (int v = 0; v < vexNum; v++) {finish[v] = false;D[v] = G.getArcs()[v0][v]; // D 记录v0到所有各个边的权值for (int w = 0; w < vexNum; w++)P[v][w] = false; // 设空路径,及设置默认值if (D[v] < INFINITY) {P[v][v0] = true; // 在P数组的第v行,标记v0被访问P[v][v] = true; // 在P数组的第v行,标记邻接点被访问}}D[v0] = 0;// 初始化,v0顶点属于S集finish[v0] = true;int v = -1;// 开始主循环,每次求得v0到某个v顶点的最短路径,并加v到S集for (int i = 1; i < vexNum; i++) {// 其余G.getVexNum-1个顶点int min = INFINITY;// 当前所知离v0顶点的最近距离for (int w = 0; w < vexNum; w++)if (!finish[w])if (D[w] < min) {v = w;min = D[w];}finish[v] = true;// 离v0顶点最近的v加入S集for (int w = 0; w < vexNum; w++)// 更新当前最短路径及距离if (!finish[w] && G.getArcs()[v][w] < INFINITY&& (min + G.getArcs()[v][w] < D[w])) { // 修改D[w]和P[w],w属于V-SD[w] = min + G.getArcs()[v][w];// w在v的基础上继续前行,所以将v经过的内容拷贝到w上System.arraycopy(P[v], 0, P[w], 0, P[v].length);P[w][w] = true;}}}public int[] getD() {return D;}public boolean[][] getP() {return P;}public static void main(String[] args) throws Exception {MGraph G = GenerateGraph.generateMGraph();ShortestPath_DIJ dij = new ShortestPath_DIJ();dij.DIJ(G, 0);dij.display(G);}// 用于输出最短路径上的各个顶点及权值public void display(MGraph G) throws Exception {if (D != null) {System.out.println("各个顶点到v0的最短路径上的点及最短距离分别是:");for (int i = 0; i < P.length; i++) {System.out.print("v0 - " + G.getVex(i) + ": ");for (int j = 0; j < P[i].length; j++) {if (P[i][j])System.out.print(G.getVex(j) + "\t");}System.out.println("最短距离为: " + D[i]);}}}}// 调试结果:
// 各个顶点到v0的最短路径上的点及最短距离分别是:
// v0 - v0: v0 最短距离为: 0
// v0 - v1: v0 v1 最短距离为: 7
// v0 - v2: v0 v2 最短距离为: 1
// v0 - v3: v0 v3 最短距离为: 5
// v0 - v4: v0 v2 v4 最短距离为: 7
// v0 - v5: v0 v2 v5 最短距离为: 5
6)迪杰斯特拉(Dijkstra)算法:性能分析
- 算法的时间复杂度:O(n2)
- 找一条从源点到某一特定终点之间的最短路径问题和求源点到各个终点的最短路径一样复杂,其时间复杂度仍为O(n2)
- 若希望得到图中任意两个顶点之间的最短路径,只要依次将每一个顶点设为源点,并调用迪杰斯特拉算法,其时间复杂度为 O(n3)
7)练习
- 练习1:
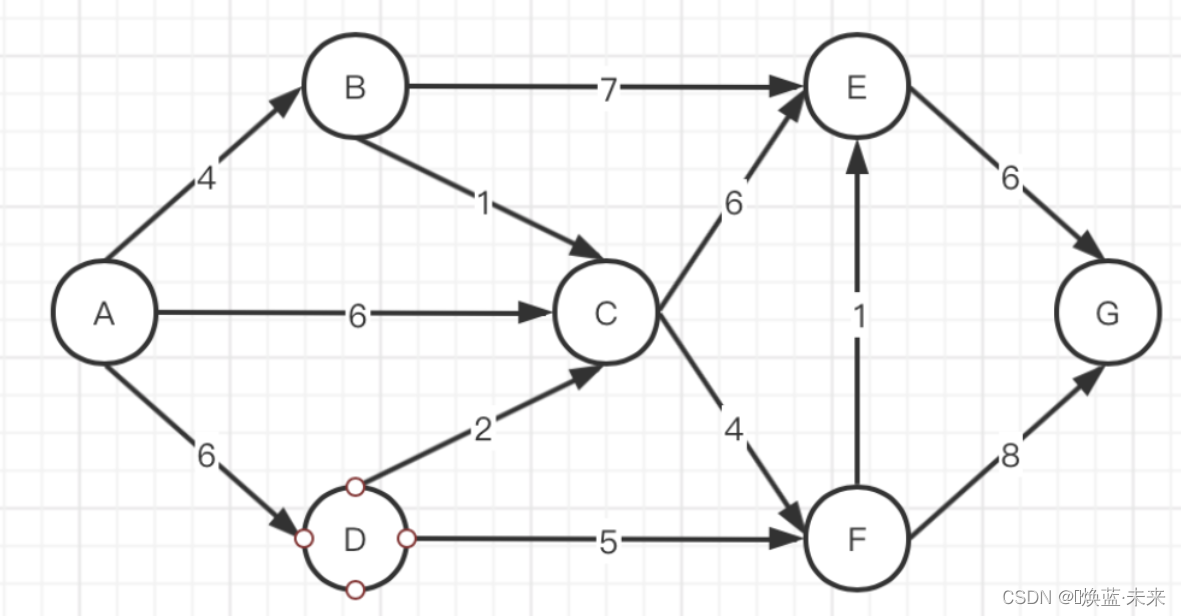
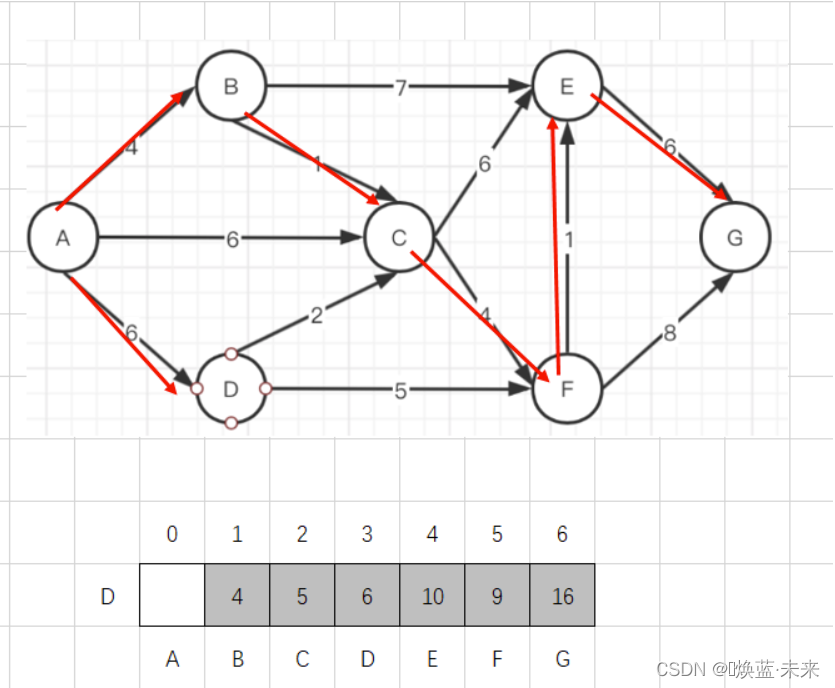
-
练习2
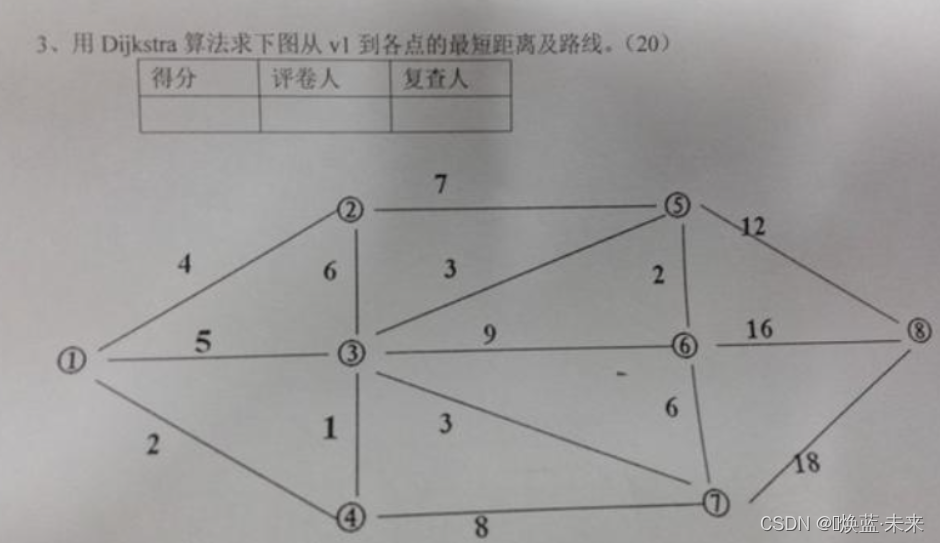
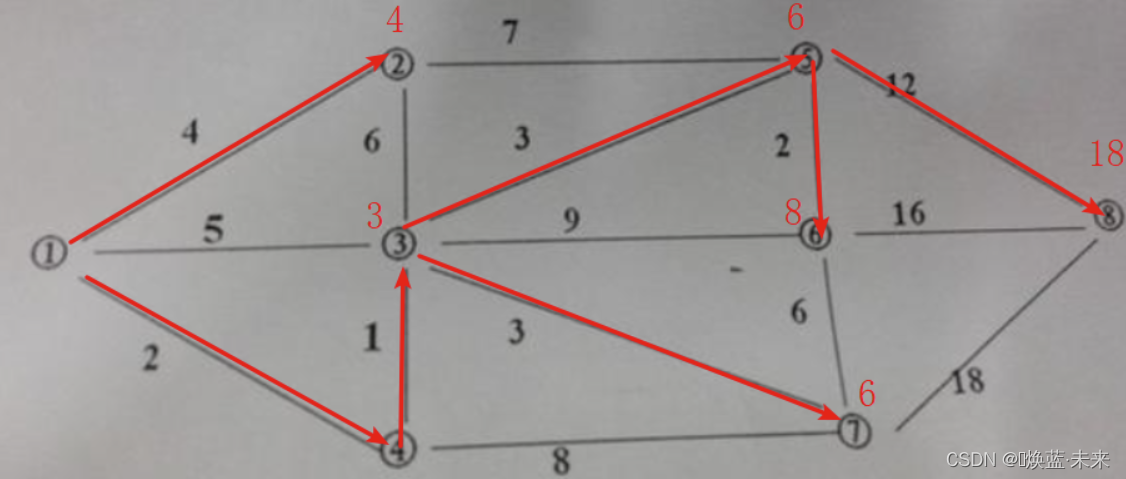
①②③④⑤⑥⑦⑧
(①,②) 最短路径:4
(①,④) 最短路径:2
(①,④,③) 最短路径:3
(①,④,③,⑤) 最短路径:6
(①,④,③,⑦) 最短路径:6
(①,④,③,⑤,⑥) 最短路径:8
(①,④,③,⑤,⑧) 最短路径:18
1.6.2 每一对顶点之间的最短路径
1)概述
-
若希望得到图中任意两个定点之间的最短路径,只要依次将每一个定点设为源点,调用迪杰斯克拉算法n次便可求得,其时间复杂度为O(n3) 。
-
佛洛依德(Floyed)提出了另外一个算法,虽然时间复杂度也是O(n3),但是算法的形式更为简单。
2)佛洛依德(Floyed) 算法:概述
- D是路径长度序列
- P是路径序列
- 求的一个n阶方阵序列:D(-1),D(0),D(1),D(2),… ,D(k),…,D(n-1)
- D(-1)[i][j]表示从顶点vi出发,不经过其他顶点【直接】到达顶点vj的路径长度。
- D(k)[i][j]表示从顶点vi到vj的中间只可能经过v0,v1,…,vk , 而不可能经过 vk+1,vk+2, … ,vn-1等顶点的最短路径长度。
- D(n-1)[i][j]表示从顶点vi到顶点vj的最短路径的长度。
3)佛洛依德(Floyed) 算法:算法分析
-
算法关键操作
// k 表示在路径中新增的顶点号 // i 表示路径的源点 // j 表示路径的终点 if(D[i][k] + D[k][j] < D[i][j]) {D[i][j] = D[i][k] + D[k][j]; //更新最短路径长度P[i][j] = P[i][k] + P[k][j]; //更新最短路径 } -
有向图
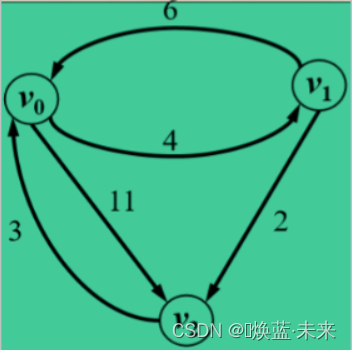
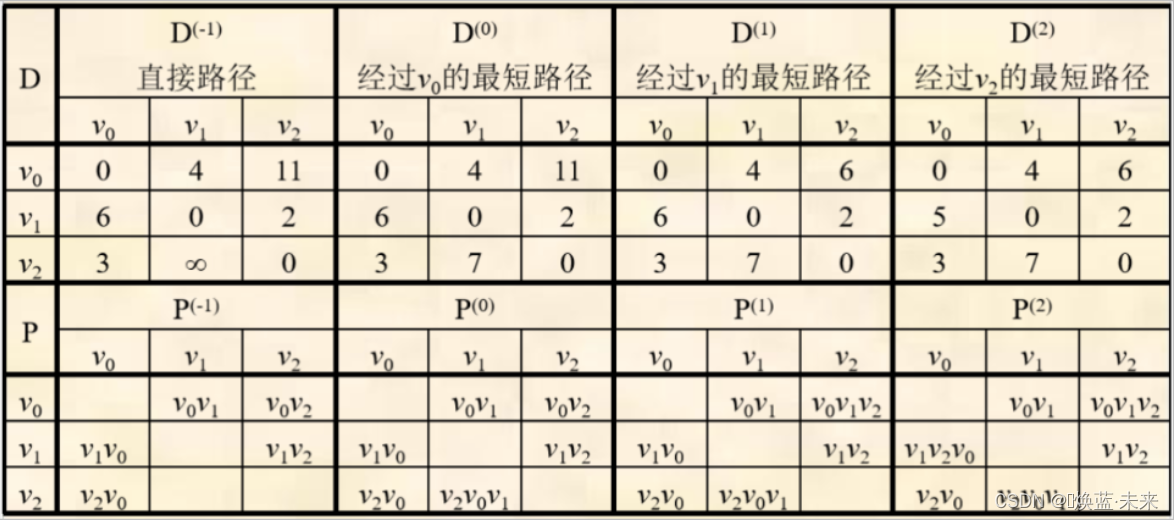
4)佛洛依德(Floyed) 算法:代码实现
- 类似于对每一个顶点进行迪杰斯特拉算法
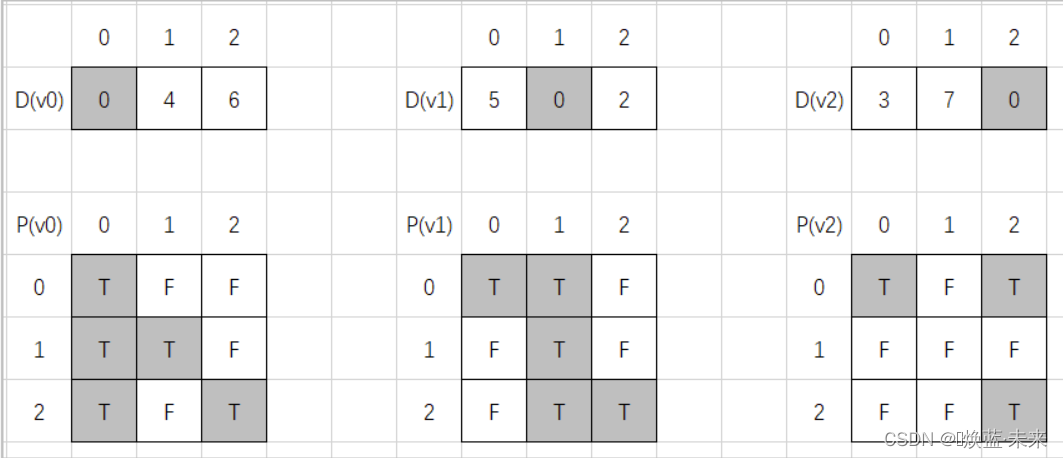
- 算法实现
package ch06;public class ShortestPath_FLOYD {private boolean[][][] P;// 顶点v和w之间的最短路径P[v][w],若P[v][w][u]为true,则u是从v到w当前求得最短路径上的顶点private int[][] D;// 顶点v和w之间最短路径的带权长度D[v][w]public final static int INFINITY = Integer.MAX_VALUE;// 用Dijkstra算法求有向网G的v0顶点到其余顶点v的最短路径P[v]及其权值D[v]public void FLOYD(MGraph G) {int vexNum = G.getVexNum();P = new boolean[vexNum][vexNum][vexNum];D = new int[vexNum][vexNum];for (int v = 0; v < vexNum; v++) // 各对结点之间初始化已知路径及距离for (int w = 0; w < vexNum; w++) {D[v][w] = G.getArcs()[v][w];for (int u = 0; u < vexNum; u++)P[v][w][u] = false;if (D[v][w] < INFINITY) {// 从v到w有直接路径P[v][w][v] = true;P[v][w][w] = true;}}for (int u = 0; u < vexNum; u++)for (int v = 0; v < vexNum; v++)for (int w = 0; w < vexNum; w++)if (D[v][u] < INFINITY && D[u][w] < INFINITY&& D[v][u] + D[u][w] < D[v][w]) { // 从v经u到w的一条路径最短D[v][w] = D[v][u] + D[u][w];for (int i = 0; i < vexNum; i++)P[v][w][i] = P[v][u][i] || P[u][w][i];}}public int[][] getD() {return D;}public boolean[][][] getP() {return P;}}
- 测试程序
package book.ch06;public class Example6_5_G9 {public final static int INFINITY = Integer.MAX_VALUE;public static void main(String[] args) throws Exception {Object vexs[] = { "v0", "v1", "v2" };int[][] arcs = { { 0, 4, 11},{ 6, 0, 2},{ 3, INFINITY,0}};MGraph G = new MGraph(GraphKind.DN, vexs.length, 5, vexs, arcs);ShortestPath_FLOYD floyd = new ShortestPath_FLOYD();floyd.FLOYD(G);display(floyd.getD());}// 输出各村的最短路径长度public static void display(int[][] D) {System.out.println("各顶点之间的最短路径长度为:");for (int v = 0; v < D.length; v++) {for (int w = 0; w < D.length; w++)System.out.print(D[v][w] + "\t");System.out.println();}}}
// 调试结果:
//各顶点之间的最短路径长度为:
// 0 4 6
// 5 0 2
// 3 7 05) 练习
- 练习1:
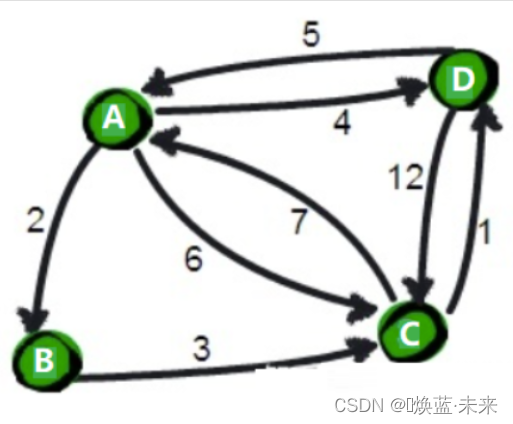
- 推导过程

-
练习2:
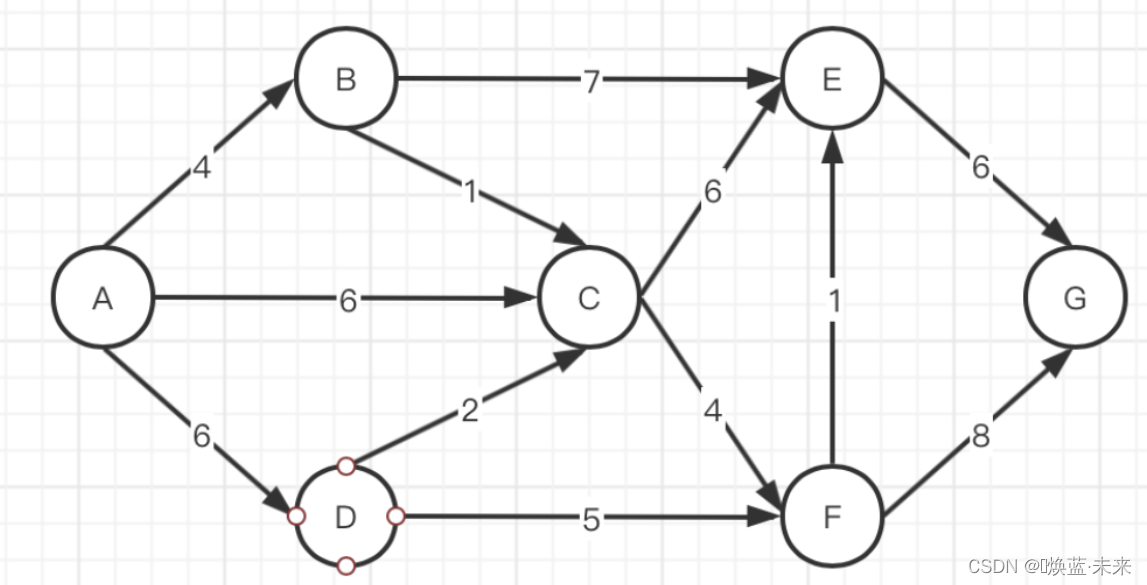
1.7 拓扑排序
1.7.1 拓扑排序:基本概念
-
问题:
- 假设以有向图表示一个工程的施工图或程序的数据流图,则图中不允许出现回路。
-
检查有向图是否存在回路的方法之一,是对有向图进行拓扑排序。
-
一个无环的有向图称为有向无环图(Directed Acycline Graph),简称为DAG图。
-
通常我们用一个有向图的顶点表示活动,边表示活动间先后关系,这样的有向图称为顶点活动网(Activity On Vertex network),简称AOV网。
- 工程是否顺利进行
- 完成整个工程所必须的最短时间
- 在AOV网表示工程的施工图,若出现环,标明该工程的施工设计图存在问题。
- 若AOV网表示的是数据流图,若出现环,标明存在死循环。
-
拓扑排序:对一个有向图构建拓扑序列的过程。
1.7.2 拓扑排序:分析
-
判断有向网是否存在有向环的一个方法:(对AOV网进行拓扑排序)
-
构造一个包含图中所有顶点的”拓扑排序序列“。
-
若在AOV网中存在一条从顶点u到顶点v的弧,则在拓扑有序序列中顶点u必然优先于顶点v。
-
若在AOV网中顶点u和顶点w之间没有弧,则在拓扑有序序列中,这两个顶点的先后次序关系可以随意
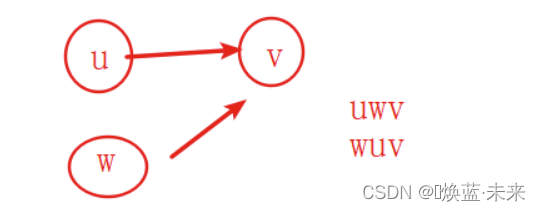
-
-
现有如下课程,并能够绘制下方有向图:
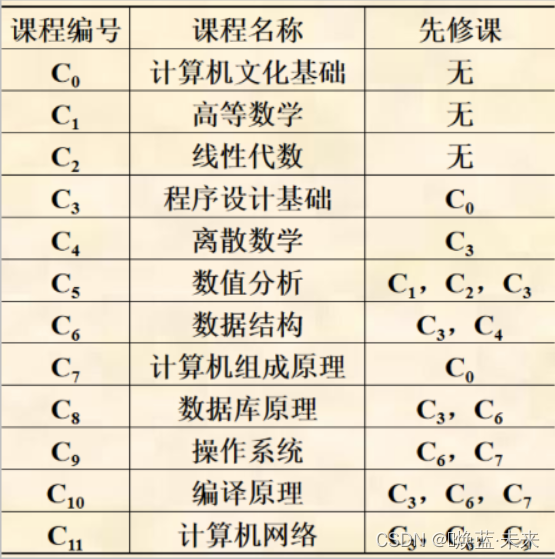
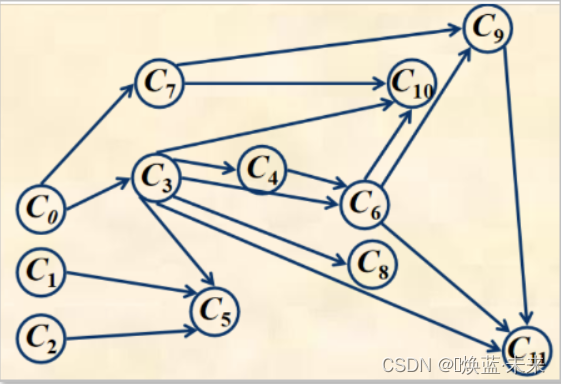
对上图的 A O V 网可以得到多个拓扑有序序列,如: C 0 、 C 1 、 C 2 、 C 3 、 C 4 、 C 5 、 C 6 、 C 7 、 C 8 、 C 9 、 C 10 、 C 11 或 C 0 、 C 1 、 C 2 、 C 7 、 C 3 、 C 5 、 C 4 、 C 6 、 C 9 、 C 8 、 C 11 、 C 10 ( ) 对上图的AOV网可以得到多个拓扑有序序列,如: \\ C_0、C_1、C_2、C_3、C_4、C_5、C_6、C_7、C_8、C_9、C_{10}、C_{11} \\ 或 \\ C_0、C_1、C_2、C_7、C_3、C_5、C_4、C_6、C_9、C_8、C_{11}、C_{10} \\ \tag{} 对上图的AOV网可以得到多个拓扑有序序列,如:C0、C1、C2、C3、C4、C5、C6、C7、C8、C9、C10、C11或C0、C1、C2、C7、C3、C5、C4、C6、C9、C8、C11、C10()
-
实例1:存在拓扑序列
abcefdgh,说明不存在环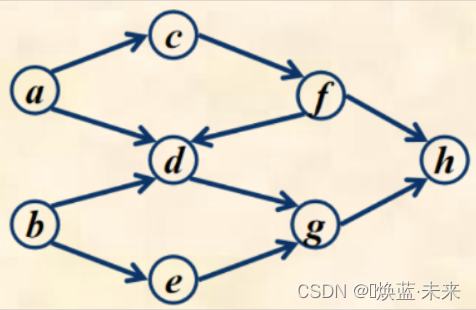
-
实例2:不存在拓扑序列,说明存在环
fdghf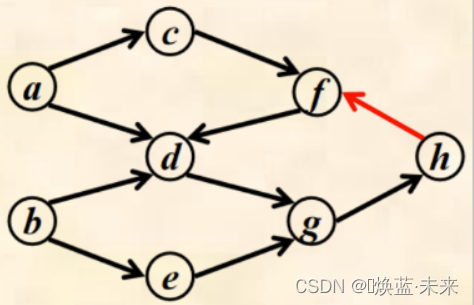
1.7.3 拓扑排序:步骤
-
步骤:
- 在AOV网中选择一个没有前驱的顶点并输出
- 从AOV网中删除该顶点以及从它出发的弧
- 重复1和2直到AOV网为空(即已输出所有的顶点),或剩余子图中不存在没有前驱的顶点。后一种情况说明该AOV网中存在有向环。
-
算法要考虑的问题:
- “没有前驱”如何判断
- “删除顶点及以它为尾的弧”如何操作
-
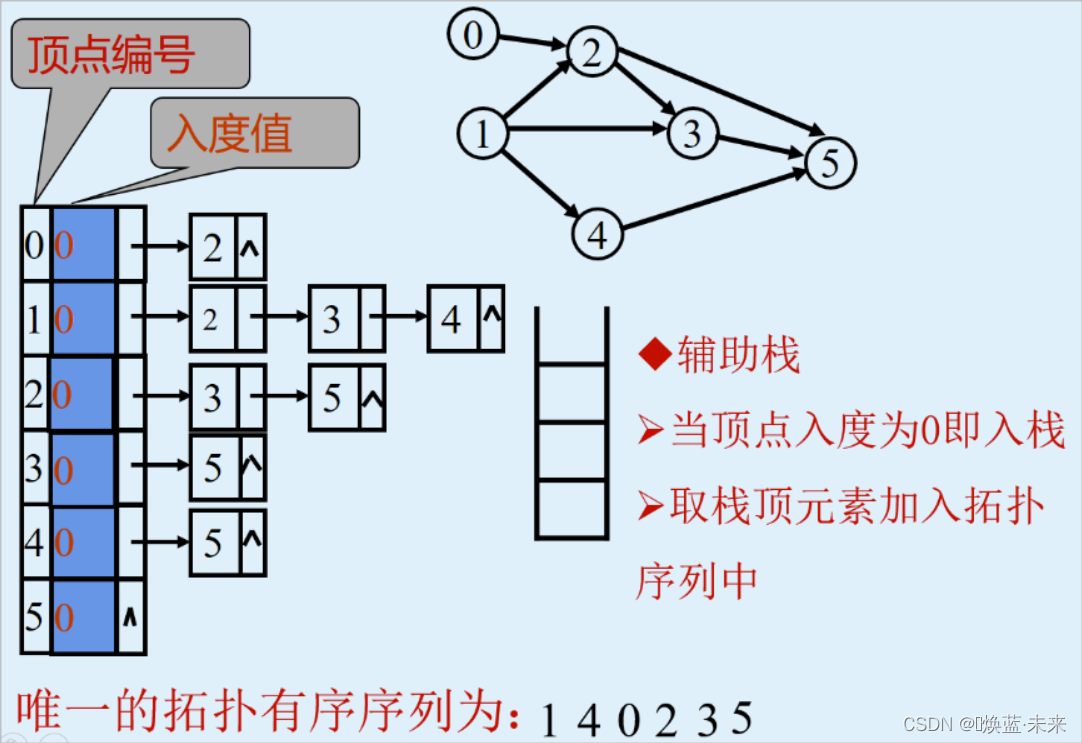
解决方法:
- 以入度为零作为没有前驱的量度
- 算法中预设一个栈,用于保存当前出现的入度为零的顶点
- 删除顶点及以它为尾的弧的这类操作,可用“弧头顶点的入度减1”的办法来替代。
-
PPT演示
1.7.4 拓扑排序:实现
- 由于拓扑排序中对图的主要操作是“找从顶点出发的弧”,并且AOV网在多数情况下是稀疏图,因此存储结构取邻接表为宜。
package ch06;import ch03.LinkStack;public class TopologicalSort {// 拓扑排序public static boolean topologicalSort(ALGraph G) throws Exception {int count = 0;// 输出定点计数int[] indegree = findInDegree(G);// 求各顶点入度LinkStack S = new LinkStack();// 建零入度顶点栈for (int i = 0; i < G.getVexNum(); i++)if (indegree[i] == 0)// 入度为0者进栈S.push(i);while (!S.isEmpty()) {int i = (Integer) S.pop(); // 栈不空 取栈顶元素System.out.print(G.getVex(i) + " ");// 输出V号顶点 并 计数++count;for (ArcNode arc = G.getVexs()[i].firstArc; arc != null; arc = arc.nextArc) {int k = arc.adjVex;if (--indegree[k] == 0)// 对i号顶点的每个邻接点的入度减1S.push(k);// 若入度减为0,则入栈}}if (count < G.getVexNum())return false;//该有向图有回路elsereturn true;}//求各顶点入度 算法6.11public static int[] findInDegree(ALGraph G) throws Exception {int[] indegree = new int[G.getVexNum()];for (int i = 0; i < G.getVexNum(); i++)for (ArcNode arc = G.getVexs()[i].firstArc; arc != null; arc = arc.nextArc)++indegree[arc.adjVex];// 入度增加1return indegree;}public static void main(String[] args) throws Exception {ALGraph G = GenerateGraph.generateALGraph();TopologicalSort.topologicalSort(G);}
}// 调试结果:
// v1 v2 v3 v5 v7 v4 v6 v8 v9
1.7.5 拓扑排序:性能分析
- 拓扑排序算法总的时间复杂度:O(n+e)
1.7.6 练习
-
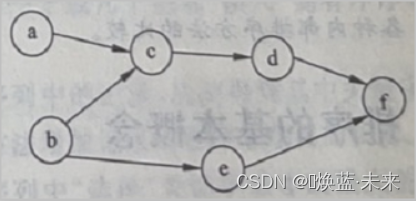
试列出下图中,全部可能的拓扑有序序列
-
参考答案:abcdef、abcedf、abecdf、bacdef、bacedf、baecdf、beacdf
1.8 关键路径
1.8.1 现实问题
-
问题:
- 假设以有向图表示一个施工流图,弧上的权值表示完成该项子工程所需时间。
- 问:整个工程完成的最短时间?以及哪些活动将是影响整个工程如期完成的关键所在?
-
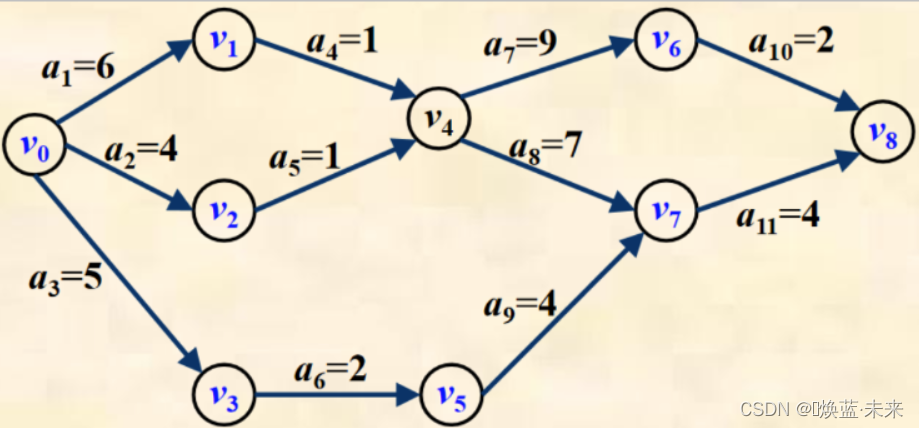
使用图描述上面情况
- 弧表示活动
- 弧上的数字表示完成该项活动所需的时间
1.8.2 相关概念
-
AOE(Activity On Edge)网:若以弧表示活动,弧上的权值表示进行该项活动所需的时间,以顶点表示事件Event,称这种有向网为边活动网络,简称为AOE。
-
事件:是一个关于某几项活动开始或完成的断言。
- 指向它的弧表示的活动已经完成。
- 而从它出发的弧表示的活动开始进行
- 整个有向图也表示了活动之间的优先关系
- 这样的有向网也是不允许存在环的
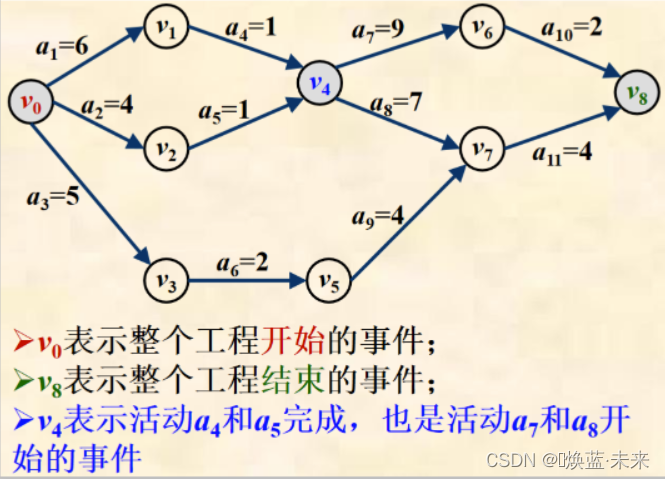
-
源点和汇点:
-
源点:表示工程开始事件的顶点的入度为零。
-
汇点:表示工程结束事件的顶点的出度为零。
-
一个工程AOE网应该是只有一个源点和一个汇点的有向无环图。
-
-
关键路径和关键活动
- 关键路径:由于AOE网中某些活动可以并行进行,故完成整个工程的最短时间即为从源点到汇点最长路径的长度,这个路径称为关键路径。
- 关键活动:构成关键路径的弧即为关键活动。
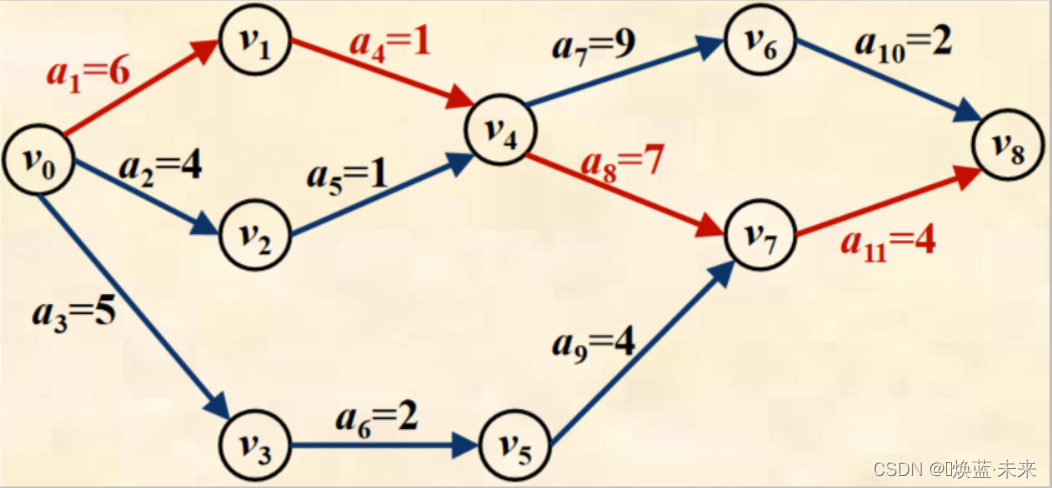
- 实例:下图工程从开始到完成需要18天
- a1、a4、a8和a11四项活动必须按时开始并按时完成,否则将延误整个工程的工期,使整个工程不能在18天内完成。
- 于是,称a1、a4、a8和a11为AOE图的关键活动。
- 由a1、a4、a8和a11构成的路径称为关键路径。
1.8.3 算法分析
-
相关概念
- 假设顶点v0为源点,vn-1 为汇点
- 时间v0的发生时刻为0时刻
- 从v0到vi的最长路径叫做事件vi的最早发生时间
- 用e(i)表示活动的最早开始时间。(这个时间决定了所有以vi为尾的弧所表示活动的最早开始时间)
- 用l(i)表示活动的最晚开始时间。
- 两者之差l(i)-e(i)意味着完成活动ai的时间余量
- 当l(i)=e(i)时的活动成为关键活动。
- 用ve(j)表示事件vj的最早开始时间。
- 用vl(j)表示事件vj的最晚开始时间。
-
关键路径和非关键路径分析
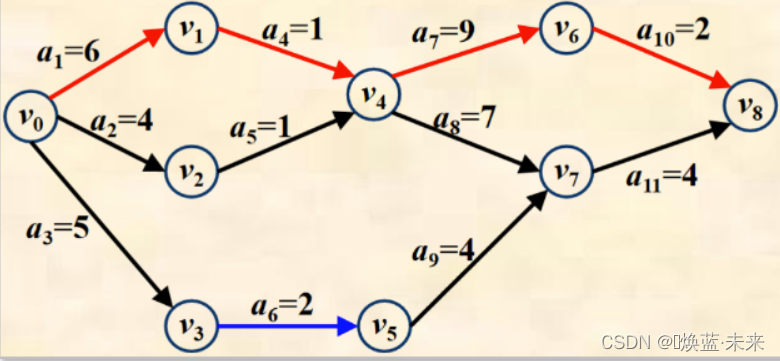
- 顶点v0到v8的一条关键路径是:(v0, v1, v4, v6, v8) ,路径长度为18。
- 活动a6不是关键活动,它的最早开始时间为5,最晚开始时间为8,时间余量为3。也就是说a6延迟3天,并不会影响整个工程的完成。
-
总结:
- 要缩短整个工程,必须先找到关键路径,提高关键活动的工效。
- 由于关键路径上的活动都是关键活动,所以,提前完成非关键活动并不能加快工程的进度。
1.8.4 算法步骤
-
从源点v0触发,令ve(0) = 0,按拓扑有序序列求其余各顶点的ve(j)=maxi {ve(i) + |vi, vj| } , <vi, vj> ∈ T,其中:T是所有以vj为头的弧的集合。若得到的拓扑有序序列中顶点的个数小于网中的顶点个数n,则说明网中有环,不能求出关键路径,算法结束。

-
从汇点vn-1出发,令vl(n-1) = ve(n-1) ,按逆拓扑有序序列求其余各顶点的 vl(i)=minj {vl(j) - |vi, vj| } , <vi, vj> ∈ S,其中:S是所有以vj为尾的弧的集合。

-
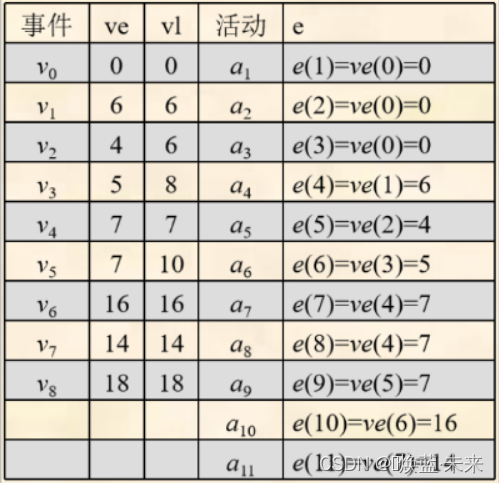
求每一项活动ai(1<=i<=n)的最早开始时间e(i)=ve(j),vj是ai的起点。
-
求每一项活动ai的最晚开始时间l(i) = vl(j) - |vi, vj| , vi是ai的起点, vj是ai的终点。
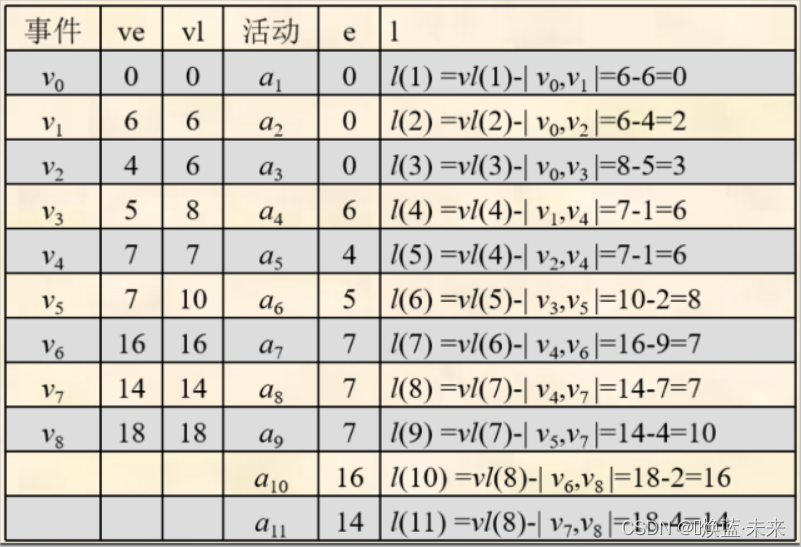
-
若对于满足e(i) = l (i) ,则它是关键活动

-
两条关键路径:
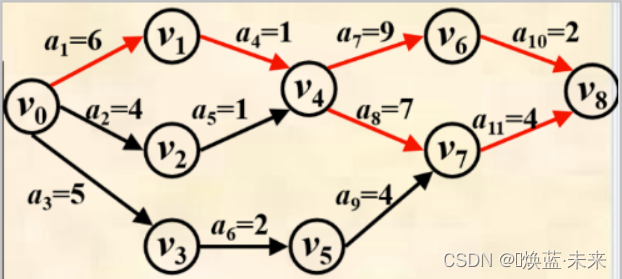
(v0, v1, v4, v6, v8)
和
(v0, v1, v4, v7, v8)
1.8.5 算法实现
package book.ch06;import book.ch03.LinkStack;public class CriticalPath {private LinkStack T = new LinkStack(); // 拓扑逆序列顶点栈private int[] ve, vl; // 各顶点的最早发生时间和最迟发生时间// 有向图G采用邻接表存储,求各顶点的最早发生时间ve,若G无回路,则用栈T返回G的一个拓扑序列,且函数返回true,否则为falsepublic boolean topologicalOrder(ALGraph G) throws Exception {int count = 0; // 输出顶点计数int[] indegree = TopologicalSort.findInDegree(G); // 求各个顶点的入度LinkStack S = new LinkStack(); // 建零入度顶点栈Sfor (int i = 0; i < G.getVexNum(); i++)if (indegree[i] == 0) // 入度为0者进展S.push(i);ve = new int[G.getVexNum()]; // 初始化while (!S.isEmpty()) {int j = (Integer) S.pop();T.push(j); // j号顶点入T栈并计数++count;for (ArcNode arc = G.getVexs()[j].firstArc; arc != null; arc = arc.nextArc) {int k = arc.adjVex;if (--indegree[k] == 0) // 对j号顶点的每个邻接点的入度减1S.push(k); // 若入度减为0,则入栈if (ve[j] + arc.value > ve[k])ve[k] = ve[j] + arc.value;}}if (count < G.getVexNum())return false; // 该有向图有回路elsereturn true;}// G为有向图,输出G的各项关键活动public boolean criticalPath(ALGraph G) throws Exception {if (!topologicalOrder(G))return false;vl = new int[G.getVexNum()];for (int i = 0; i < G.getVexNum(); i++)// 初始化顶点时间的最迟发生时间vl[i] = ve[G.getVexNum() - 1];while (!T.isEmpty()) { // 按拓扑逆序列求各顶点的vl值int j = (Integer) T.pop();for (ArcNode arc = G.getVexs()[j].firstArc; arc != null; arc = arc.nextArc) {int k = arc.adjVex;int value = arc.value;if (vl[k] - value < vl[j])vl[j] = vl[k] - value;}}System.out.println("ve:事件最早发生时间、vl事件最晚发生时间");System.out.println("事件ve\tvl");for (int j = 0; j < G.getVexNum(); j++) {int ee = ve[j];int el = vl[j];System.out.println(G.getVex(j) + "\t" + ee + "\t" + el); // 输出关键事件}System.out.println("e:活动最早开始时间、l:活动最晚开始时间");System.out.println("源点-->\t汇点权值\te\tl\tl-e\t关键活动");for (int j = 0; j < G.getVexNum(); j++)// 求ee,el和关键活动for (ArcNode arc = G.getVexs()[j].firstArc; arc != null; arc = arc.nextArc) {int k = arc.adjVex;int value = arc.value;int ee = ve[j];int el = vl[k] - value;char tag = (ee == el) ? '*' : ' ';System.out.println(G.getVex(j) + "\t->\t" + G.getVex(k) + "\t"+ value + "\t" + ee + "\t" + el + "\t" + (el-ee) + "\t" + tag); // 输出关键活动}return true;}public static void main(String[] args) throws Exception {ALGraph G = GenerateGraph.generateALGraph();CriticalPath p = new CriticalPath();p.criticalPath(G);}
}// 调试结果:
//ve:事件最早发生时间、vl事件最晚发生时间
//事件 ve vl
//v0 0 0
//v1 6 6
//v2 4 6
//v3 5 8
//v4 7 7
//v5 7 10
//v6 16 16
//v7 14 14
//v8 18 18
//e:活动最早开始时间、l:活动最晚开始时间
//源点--> 汇点 权值 e l l-e 关键活动
//v0 -> v3 5 0 3 3
//v0 -> v2 4 0 2 2
//v0 -> v1 6 0 0 0 *
//v1 -> v4 1 6 6 0 *
//v2 -> v4 1 4 6 2
//v3 -> v5 2 5 8 3
//v4 -> v7 7 7 7 0 *
//v4 -> v6 9 7 7 0 *
//v5 -> v7 4 7 10 3
//v6 -> v8 2 16 16 0 *
//v7 -> v8 4 14 14 0 *=========================================================
后记

好啦,以上就是本期全部内容,能看到这里的人呀,都是能人。
十年修得同船渡,大家一起点关注。
我是♚焕蓝·未来,感谢各位【能人】的:点赞、收藏和评论,我们下期见!
各位能人们的支持就是♚焕蓝·未来前进的巨大动力~
注:如果本篇Blog有任何错误和建议,欢迎能人们留言!
这篇关于数据结构与算法——图篇详解的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





