POJ-2870 Light Up + DFS(1级DFS+1级DFS) + Python

参考链接：poj2870Light Up(迭代加深搜索)_ophunter的专栏-CSDN博客

一 说明：

1.1 题目大致意思是：放置灯以照亮整个矩阵，返回所需灯的最小数量。

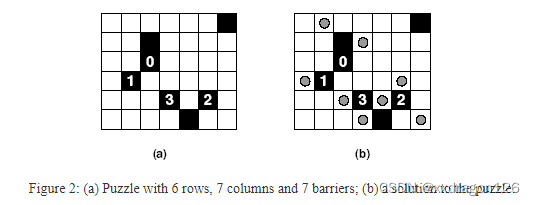
         给定一个矩阵如图(a)所示，其中黑色方框表示障碍物，障碍物的编号表示其周围需要的灯的数量(无编号的障碍物所需的灯数不限)；除此之外，空白网格所在行列也需要有灯存在，以便于照亮该空白网格。

1.2 由于涉及寻找所有方案，所以确定本题用DFS解决。

1.2.1 将问题分解为两级DFS：

        第一级：以障碍物所需灯数为目标，寻找所有“照亮障碍物“”的安灯方案

        第二级：对第一级结果中的每一个方案进行安灯，以“照亮剩余的空白网格”。

        因此，两级方案所需的最小灯数，即为答案。

1.2.2 设计原理及注意事项

## 0 程序设计时，用不同数值的元素值反映各个信息：

        空白用-10表示，

        照亮后的行、列空白用-20表示，

        点灯位置赋值为-30。
## 1 编号为0的障碍物的4邻域为禁区，不能放置灯；
## 2 以编号最大的障碍物的邻接点为初始顶点，进行DFS搜索；
## 3 对当前障碍物的邻点放置灯时，该灯周围如果有其他障碍物，也将被照亮；
## 4 本题分为2级DFS：第一级，为障碍物点灯，寻找所有可行的方案；第二级，对各个可行方案中的空白点灯
## 4.1 在确定障碍物的点灯方案后，当对空白网格进行点灯时，灯的周围不能有障碍物，否则将使得障碍物的点灯方案有误。
## 4.1.1 如果为空白网格点灯时，其周围存在障碍物，则将该位置赋值为-100；再继续对其他空白进行点灯，直到无-10存在。最后，判断是否有-100，无-100说明点灯成功。
# # 5. 终止条件
# # 第一级dfs：所有障碍物的所需点灯均已安装完毕
# # 第二级dfs:  所有空白格均已点灯完毕
# # 6 本程序需要查询所有方案，不能使用return True or False，而是使用 return。

1.2.3 其他注意事项：

1.3 关键问题在于实施细节。

1.3.1 本人用了整整3天才做完。太菜了。代码超长。

1.3.2 我觉得应该绘制一个思维导图，用于呈现本题的程序流程，否则数天之后，本人将不记得这程序的设计逻辑。

1.4 思维导图有点可怕：

1.4.1 总图

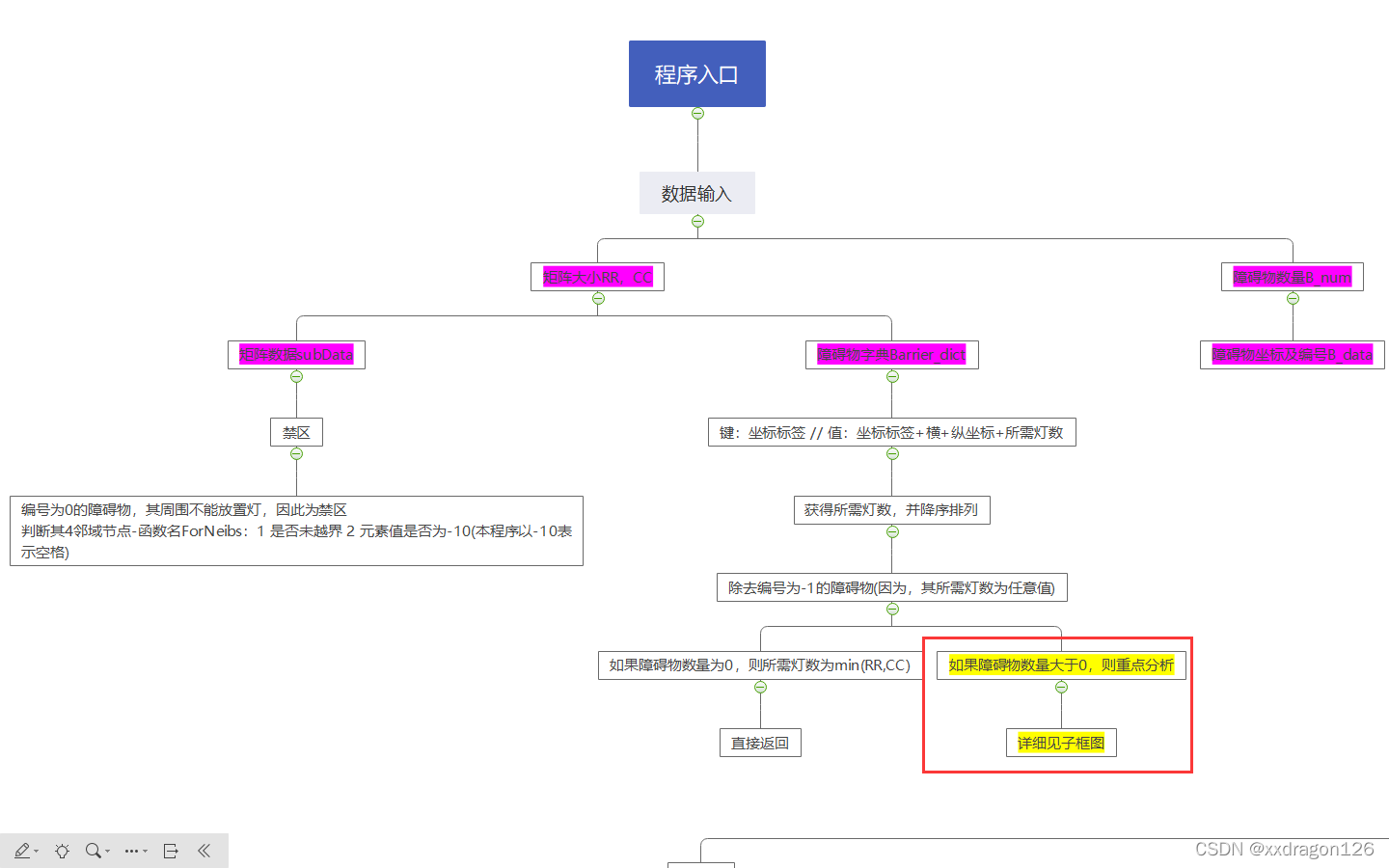
 1.4.2 

查看PDF吧，实在是太庞大了。

POJ-2870LightUp+DFS(1级DFS+1级DFS)+Python-思维导图-互联网文档类资源-CSDN下载

1.4.3 或许应该写成Word文档。

二 代码实现

# poj2870Light Up(迭代加深搜索)
# https://blog.csdn.net/ophunter_lcm/article/details/9318079?locationNum=10&fps=1&utm_medium=distribute.pc_relevant.none-task-blog-2~default~baidujs_title~default-0.no_search_link&spm=1001.2101.3001.4242.1
## 结果正确，但是，太耗时了。考虑，将重复的方案去掉。
##
# 试一试吧 20211221 2108
## 0 程序设计时，用不同大小的元素值反映各个信息：空白用-10表示，照亮后的行。列空白用-20表示，点灯位置赋值为-30。
## 1 编号为0的障碍物的邻域为禁区，不能放置灯
## 2 以编号最大的障碍物的邻接点为初始顶点，进行DFS搜索
## 3 对当前障碍物的邻点放置灯时，该灯周围如果有其他障碍物，也将被照亮
## 4 本题分为2级DFS：第一级，为障碍物点灯，寻找所有可行的方案；第二级，对各个可行方案中的空白点灯
## 4.1 在确定障碍物的点灯方案后，当对空白网格进行点灯时，灯的周围不能有障碍物，否则将使得障碍物的点灯方案有误。
## 4.1.1 如果为空白网格点灯时，其周围存在障碍物，则将该位置赋值为-100；再继续对其他空白进行点灯，直到无-10存在。最后，判断是否有-100，无-100说明点灯成功。
# 5. 终止条件
# # 第一级dfs：所有障碍物的所需点灯均已安装完毕
# # 第二级dfs:所有空白格均已点灯完毕
# 6 需要查询所有方案的时候，应该不能使用return True or False，而是使用 return# # 一些约束条件：
# 1. 障碍旁边的灯的个数与其编号相同
# 2. 同一行或列最多是有一个灯，即已经被点亮的地方，不能再放置灯
# 3. 所有的空白均被照亮
# 4. 灯可以照亮未被障碍堵塞的整行或整列# 8 迭代返回和终止的条件是什么？
import collections
import math
#1.1 数据转化
# 1.1 注意障碍数是否为0
# 1.2 注意将障碍的横纵坐标均减去1，再进行赋值
def sub2Dict(RR,CC,B_num,B_data):##subData = [[-10]*CC for i in range(RR)] # # # 空白用-10表示## 1 将障碍添加到数据矩阵中，同时获得障碍矩阵Barrier_dict = collections.defaultdict(list)if B_num > 0:for bi in range(B_num):rr,cc,kk = map(int,B_data[bi].strip().split(' '))subData[rr-1][cc-1] = kk # 横纵坐标减去1，使之从下表0开始编号# Barrier_dict[kk] = [str(rr-1)+';'+str(cc-1),rr-1,cc-1,kk] # 坐标索引，横坐标、纵坐标、所需的灯数 # 隐患：只保存一次-1障碍，本字典记录的障碍数小于实际数Barrier_dict[str(rr - 1) + ';' + str(cc - 1)] = [str(rr - 1) + ';' + str(cc - 1), rr - 1, cc - 1, kk]## 将数据转化为dictData_dict = collections.defaultdict(list)Stop_dict = collections.defaultdict(list) # 需要提前设置该空值for ri in range(RR):for ci in range(CC):# 0 获得元素坐标Data_dict[str(ri)+';'+str(ci)] = subData[ri][ci]## 1 查找编号为0的元素的邻域，它的空位置领域，不能放置灯，即得到禁区的坐标if subData[ri][ci] == 0:Stop_dict = ForNeibs(ri, ci, RR, CC, subData)return subData,Data_dict,Stop_dict,Barrier_dict
## 查找节点的可用邻域
def ForNeibs(ri,ci,RR,CC,subData):Neib_Dict = collections.defaultdict(list)## 查找当前节点的有效的4邻域，且只有其为空格时才属于有效的潜在置灯位置## 是否加入，不属于禁区呢？if 0 <= ri + 1 <= RR - 1 and subData[ri + 1][ci] == -10:node1 = str(ri + 1) + ';' + str(ci)Neib_Dict[node1] = [subData[ri + 1][ci]]if 0 <= ri - 1 <= RR - 1 and subData[ri - 1][ci] == -10:node1 = str(ri - 1) + ';' + str(ci)Neib_Dict[node1] = [subData[ri - 1][ci]]if 0 <= ci + 1 <= CC - 1 and subData[ri][ci + 1] == -10:node1 = str(ri) + ';' + str(ci + 1)Neib_Dict[node1] = [subData[ri][ci + 1]]if 0 <= ci - 1 <= CC - 1 and subData[ri][ci - 1] == -10:node1 = str(ri) + ';' + str(ci - 1)Neib_Dict[node1] = [subData[ri][ci - 1]]return Neib_Dict
## 查找节点的可用邻域
def ForNeibs2(ri,ci,RR,CC,subData,stop_keys):Neib_Dict = collections.defaultdict(list)## 查找当前节点的有效的4邻域，且只有其为空格时才属于有效的潜在置灯位置## 是否加入，不属于禁区呢？if 0 <= ri + 1 <= RR - 1 and subData[ri + 1][ci] == -10 and str(ri + 1) + ';' + str(ci) not in stop_keys:node1 = str(ri + 1) + ';' + str(ci)Neib_Dict[node1] = [subData[ri + 1][ci]]if 0 <= ri - 1 <= RR - 1 and subData[ri - 1][ci] == -10 and str(ri - 1) + ';' + str(ci) not in stop_keys:node1 = str(ri - 1) + ';' + str(ci)Neib_Dict[node1] = [subData[ri - 1][ci]]if 0 <= ci + 1 <= CC - 1 and subData[ri][ci + 1] == -10 and str(ri) + ';' + str(ci + 1) not in stop_keys:node1 = str(ri) + ';' + str(ci + 1)Neib_Dict[node1] = [subData[ri][ci + 1]]if 0 <= ci - 1 <= CC - 1 and subData[ri][ci - 1] == -10 and str(ri) + ';' + str(ci - 1) not in stop_keys:node1 = str(ri) + ';' + str(ci - 1)Neib_Dict[node1] = [subData[ri][ci - 1]]return Neib_Dict
##
class Solution:def DFS(self):# 2 获得禁区字典temp = []for stop_keys in Stop_dict.keys():temp.append(stop_keys)self.stop_keys = temp# 3 获得障碍区字典temp = []temp2 = []for barrier_keys in Barrier_dict.keys():temp.append(barrier_keys)temp2.append(Barrier_dict[barrier_keys][3])self.barrier_keys = temp####1 以障碍区的编号数为基准进行第一轮搜索self.keys_queue = sorted(set(temp2), reverse=True)  # 降序排列if -1 in set(self.keys_queue):  # 则不考虑-1障碍周围的灯数self.keys_queue = self.keys_queue[:-1]## 判断长度是否为0if len(self.keys_queue) == 0:  # 即没有任何障碍return min(RR, CC)elif len(self.keys_queue) > 0:## 这里新设置一个障碍字典，用来存放以“障碍序号”为键值的障碍信息，其中不包括编号为-1的障碍new_Barrier_dict = collections.defaultdict(list)for ki in Barrier_dict.keys():if Barrier_dict[ki][3] in self.keys_queue:new_Barrier_dict[Barrier_dict[ki][3]] = Barrier_dict[ki]# if 0 not in set(self.keys_queue):  # 当不存在0障碍时，则不能使用禁区字典Stop_dict#     Stop_Flag = False# subData,Data_dict,Stop_dict,Barrier_dict## 开始处理：## 以编号最大的障碍的可用邻域作为初始点，分别计算各初始点情况下，所能获得的最小值。node = self.keys_queue[0]node_rr, node_cc = new_Barrier_dict[node][1], new_Barrier_dict[node][2]  # 当前障碍点的坐标Neib_Dicts = ForNeibs(node_rr, node_cc, RR, CC, subData)  # 当前障碍点的可用的邻域self.waysOFbarrier = []self.lampsOFwys = []# ans_step = [math.inf]if len(Neib_Dicts)>= new_Barrier_dict[node][3]:# 说明可以放置灯for ni in Neib_Dicts.keys():  # 4邻域中的可用坐标点# 判断是否不位于禁区if ni not in self.stop_keys:  # 不位于禁区# 0 设置所需灯数的初始值self.Barrier_lamps = math.inf # 障碍灯数# 1 获得当前的坐标ni_rr, ni_cc = map(int, ni.strip().split(';'))Init_lamps = []# Flag,steps = self.dfs(node,ni_rr,ni_cc,subData, Data_dict,new_Barrier_dict, Init_lamps)self.dfs(ni_rr, ni_cc, subData, new_Barrier_dict, Init_lamps)# ans_step.append(self.Max_lamps)# 这里应该存储并比较dfs的返回结果# Flag表示当前的节点下，是否存在可行的方案# steps表示当前节点下，可能方案的灯数。else:# 说明不足以放置所需数目的灯return math.inf## 接下来，再对获得方案进行第二轮dfs处理，实现对所有空格的点亮##ANS_steps = []Len_ans = len(self.waysOFbarrier)## 剔除重复方案Ans_ways_set = set()# Ans_ways_set.add('None')Ans_ways_final = []Ans_ways_lampa = []Ans_ways_index = []for ai in range(Len_ans):# 转化为一维数组zl_series = ''for si in range(RR):for sj in range(CC):zl_series = zl_series + str(self.waysOFbarrier[ai][si][sj])zl = zl_seriesif zl not in Ans_ways_set:Ans_ways_set.add(zl_series)Ans_ways_final.append(self.waysOFbarrier[ai])Ans_ways_lampa.append(self.lampsOFwys[ai])Ans_ways_index.append(ai)Len_ans = len(Ans_ways_final)for ai in range(Len_ans):# 获得方案结果和已经点亮的灯数new_Data = Ans_ways_final[ai]Cur_Barrier_lamps = Ans_ways_lampa[ai]# #1 获得空位置的节点：empty_dict = self.FindEmpty(new_Data)self.Max_lamps = math.infif len(empty_dict) == 0:# 为0则终止if self.Max_lamps > Cur_Barrier_lamps+0:self.Max_lamps = Cur_Barrier_lamps + 0ANS_steps.append(self.Max_lamps)break # 进行下一次循环else:empty_step = [math.inf]for keyy in empty_dict.keys(): # 循环对每个节点进行分析，查找这些方案下能获得的最小的灯数self.Max_empty_steps = math.infni_rr, ni_cc = map(int, keyy.strip().split(';')) # 获得当前节点的坐标Init_empty_lamps = []self.dfs2(ni_rr, ni_cc,new_Data,empty_dict,Init_empty_lamps)empty_step.append(self.Max_empty_steps)### zl = min(empty_step)if Cur_Barrier_lamps + min(empty_step) < self.Max_lamps :self.Max_lamps = Cur_Barrier_lamps + min(empty_step)ANS_steps.append(self.Max_lamps)return min(ANS_steps)# def dfs(self,parent_node,ni_rr,ni_cc,Data,data_dict,barrier_dict,lamps):def dfs(self, ni_rr, ni_cc, Data, barrier_dict, lamps):# （一）## 用于存放错误的点灯位置# Error_lams = []## 0  传递数据，存储灯的位置new_lamps = []## 0.1 存储当前该灯的位置lamp_str = str(ni_rr) + ';' + str(ni_cc);if lamp_str not in self.stop_keys:new_lamps.append(lamp_str) ## 首先加入一个新元素else:return False,0for lap in lamps:  # 继承原来的灯if lap not in self.stop_keys:new_lamps.append(lap) ## 然后再逐个加入## 0 传递数据new_Data = self.Render(ni_rr, ni_cc, Data)# ## 0 传递字典数据；用来更新障碍周围所需的灯数new_barrier_dict = {}for keyi in barrier_dict.keys():new_barrier_dict[keyi] = barrier_dict[keyi][::]# 照亮周围的障碍物# 当前节点的四邻域Lit_Flag,new_barrier_dict = self.LitupBarrier(ni_rr, ni_cc, RR, CC, new_barrier_dict)if Lit_Flag == False: # 说明点灯失败return# new_barrier_dict[parent_node][3] = new_barrier_dict[parent_node][3] - 1;#### 能否在此处进行判断呢？# （二）## 判断一下是否终止了：判断障碍周围是否已经放置了所需数据的灯Lamp_needed = Truefor barri in self.keys_queue:if new_barrier_dict[barri][3] != 0:Lamp_needed = Falsebreakif Lamp_needed == True:  # 说明障碍物旁边的所需灯已经放置完毕，接下来需要对其他的空白节点进行放置## 当前终止之后，还要再嵌套一个dfs用来填充之后的-10空格，直到矩阵中再无-10元素## 当前所需的灯的数量LEN = len(new_lamps)if self.Barrier_lamps > LEN:self.Barrier_lamps = LEN#####保存当前方案及其所需的灯数self.waysOFbarrier.append(new_Data) # 这里不应该有缩进的，否则有些可能的方案不能保存。self.lampsOFwys.append(LEN)# return True,self.Barrier_lampsreturn # 这里也不要有缩进了。## 循环分析for node in self.keys_queue:if node != max(self.keys_queue):#如果编号更大的障碍物所需灯数没有实现，则返回if new_barrier_dict[node+1][3] !=0: # 说明未找到合适的方案 // 加入这条判断，有助于加速，避免获得重复的方案。returnnode_rr, node_cc = new_barrier_dict[node][1], new_barrier_dict[node][2]  # 当前障碍点的坐标# 获得当前障碍的候选点灯节点Neib_Dicts = ForNeibs(node_rr, node_cc, RR, CC, new_Data)  # 当前障碍点的可用的邻域if len(Neib_Dicts) == new_barrier_dict[node][3] and new_barrier_dict[node][3]>0 :  # 说明可以放置灯for ni in Neib_Dicts.keys():  # 4邻域中的可用坐标点# 判断是否不位于禁区if ni not in self.stop_keys:if ni not in new_lamps:  # 不位于禁区，并且未被点亮# 获得当前的坐标ni_rr, ni_cc = map(int, ni.strip().split(';'))# 判断当前行列中，是否存在已点亮的灯，如果有的话，说明之前的这个灯放错了，应该记录下来，在递归返回时，将其位置恢复原状，并添加到禁止访问区域中Error_lams = self.D_ErrorL(ni_rr, ni_cc,new_lamps)if len(Error_lams)>0:## 如果存在冲突，则返回return# for ei in Error_lams:#     self.stop_keys.append(ei) # 不能添加进来，因为这有可能是错误方案导致的。# 将每个点填充到数据中## 这里设置一个程序，将灯所在行列全部赋值-20（被遮挡的区域除外）new_Data = self.Render(ni_rr, ni_cc,new_Data)## 存储该灯的位置# new_lamps = []new_lamps.append(str(ni_rr) + ';' + str(ni_cc))# 记录已点的灯数Lit_Flag, new_barrier_dict = self.LitupBarrier(ni_rr, ni_cc, RR, CC, new_barrier_dict)if Lit_Flag == False:  # 说明点灯失败return# new_barrier_dict[node][3] = new_barrier_dict[node][3] -1; # 每点灯一次，其所需灯数少1else:# return False, 0returnelif len(Neib_Dicts) < new_barrier_dict[node][3] and new_barrier_dict[node][3] >0:# return False, 0# 说明无法获得满足需求的灯，直接结束吧！returnelif len(Neib_Dicts) > new_barrier_dict[node][3] and new_barrier_dict[node][3]>0: # 当需要点灯，并且有可用的点灯区域时# 这里需要迭代处理吧for ni in Neib_Dicts.keys(): # 4邻域中的可用坐标点# 判断是否不位于禁区if ni in self.stop_keys:# 有位于禁区的邻点，不符合要求，寻找下一个continueelse: # 需要迭代处理吗# 获得当前的坐标ni_rr, ni_cc = map(int, ni.strip().split(';'))## 这里需要判断：# 1. 何时更新新的灯队列（建议在进入循环之后判断）# 2. 何时判断，当前行列中是否已经有灯了（建议此时判断）Error_lams = self.D_ErrorL(ni_rr, ni_cc, new_lamps)if len(Error_lams)>0:break # 说明此时ni所在行或列已经有灯了，不再进行后续处理else:## 接下来应该要进入递归循环了self.dfs(ni_rr, ni_cc, new_Data, new_barrier_dict, new_lamps)return## 设计第二个dfsdef dfs2(self,ni_rr, ni_cc, Data, empty_dict,lamps):# 1 传递数据，并存储当前灯的位置new_lamps = []str1 = str(ni_rr)+';'+str(ni_cc)if str1 not in self.stop_keys:new_lamps.append(str1)  ## 首先加入当前的新元素else:returnfor lap in lamps:  # 继承原来的灯if lap not in self.stop_keys:new_lamps.append(lap)  ## 然后再逐个加入# 2 传递，并更新当前的数据# 2.1 特别注意：当前行列不能有其他灯# 2.2 照亮整行和整列，除非遇到障碍物(在本例中，只要连续地遇到-10、-20，就照亮；遇到其他元素，就停止照亮)new_Data = self.Render2(ni_rr, ni_cc, Data)# 2.3 进一步判断，如果当前点的4邻域有已编号的障碍物，则不能点亮# 3 获得新的空格坐标new_empty_dict = self.FindEmpty(new_Data)# 3.1 如果为空，则终止if len(new_empty_dict) == 0: # 说明已经没有-10空位置了，但不说明成功了，因为有些点可能不能用来点亮，被设置成了-100# 1 检查是否存在-100 元素# 1.1 转成一串数组zl_series = set()for si in range(RR):for sj in range(CC):zl_series.add(new_Data[si][sj])# 1.2 判断是否有-100if -100 in zl_series:self.Max_empty_steps = math.infreturnelse:# 说明全部已经点亮if len(new_lamps) < self.Max_empty_steps:self.Max_empty_steps = len(new_lamps)return##else:# 进入下一次循环## 检测空位置：for ei in new_empty_dict.keys():ei_rr, ei_cc = map(int, ei.strip().split(';'))  # 获得当前节点的坐标self.dfs2(ei_rr, ei_cc,new_Data,new_empty_dict,new_lamps)return## 照亮空格## 检测当前点灯的位置周围是否存在有编号的障碍物def Render2(self, ni_rr, ni_cc, Data):# 首先，使用该方法将原始矩阵赋值给新矩阵new_Data = []for rr in range(len(Data)):temp = []for cc in range(len(Data[0])):temp.append(Data[rr][cc])new_Data.append(temp)## 1 检测当前点灯的位置周围是否存在有编号的障碍物if self.decteBarrier(ni_rr, ni_cc) == False:  # False:表示有障碍物# 则将其赋值为-100，并返回new_Data[ni_rr][ni_cc] = -100return new_Dataelse:### 1 点亮当前行的各列元素for ci in range(ni_cc, CC):if new_Data[ni_rr][ci] == -10 or new_Data[ni_rr][ci] == -20 or new_Data[ni_rr][ci] == -100:new_Data[ni_rr][ci] = -20;  # 点亮，即赋值为-20else:break  # 遇到其他元素则终止点亮for ci in range(ni_cc, -1, -1):if new_Data[ni_rr][ci] == -10 or new_Data[ni_rr][ci] == -20 or new_Data[ni_rr][ci] == -100:new_Data[ni_rr][ci] = -20;  # 点亮，即赋值为-20else:break  # 遇到其他元素则终止点亮## 2 点亮当前列的各行元素for ri in range(ni_rr, RR):if new_Data[ri][ni_cc] == -10 or new_Data[ri][ni_cc] == -20 or new_Data[ri][ni_cc] == -100:new_Data[ri][ni_cc] = -20;  # 点亮，即赋值为-20else:break  # 遇到其他元素则终止点亮for ri in range(ni_rr, -1, -1):if new_Data[ri][ni_cc] == -10 or new_Data[ri][ni_cc] == -20 or new_Data[ri][ni_cc] == -100:new_Data[ri][ni_cc] = -20;  # 点亮，即赋值为-20else:break  # 遇到其他元素则终止点亮## 返回点亮后的元素new_Data[ni_rr][ni_cc] = -30return new_Data## 这个解决方案可能存在问题。def decteBarrier(self,ri,ci):Neib_Dict = []if 0 <= ri + 1 <= RR - 1:node1 = str(ri + 1) + ';' + str(ci)Neib_Dict.append(node1)if 0 <= ri - 1 <= RR - 1:node1 = str(ri - 1) + ';' + str(ci)Neib_Dict.append(node1)if 0 <= ci + 1 <= CC - 1:node1 = str(ri) + ';' + str(ci + 1)Neib_Dict.append(node1)if 0 <= ci - 1 <= CC - 1:node1 = str(ri) + ';' + str(ci - 1)Neib_Dict.append(node1)## 判断是否有障碍物for bi in Barrier_dict.keys():if Barrier_dict[bi][0] in Neib_Dict and Barrier_dict[bi][3] !=-1:  # 说明当前点的周围有障碍物，且障碍物有编号，因此不能点灯return Falsereturn True## 查找空格def FindEmpty(self,new_Data):empty_dict = collections.defaultdict(list)for rr in range(RR):for cc in range(CC):if new_Data[rr][cc] == -10:str1 = str(rr)+';'+str(cc)empty_dict[str1] = [str1,rr,cc]return empty_dict## 当前节点的四邻域，是否存在障碍物def LitupBarrier(self,ri, ci, RR, CC,new_barrier_dict):# 对当前的点灯位置进行分析，判断其周围是否有障碍# 如果周围有障碍0，则返回错误# 对于编号大于0的障碍，均减去1，并且减1之后，不能为负数Neib_Dict = []if 0 <= ri + 1 <= RR - 1:node1 = str(ri + 1) + ';' + str(ci)Neib_Dict.append(node1)if 0 <= ri - 1 <= RR - 1:node1 = str(ri - 1) + ';' + str(ci)Neib_Dict.append(node1)if 0 <= ci + 1 <= CC - 1:node1 = str(ri) + ';' + str(ci + 1)Neib_Dict.append(node1)if 0 <= ci - 1 <= CC - 1:node1 = str(ri) + ';' + str(ci - 1)Neib_Dict.append(node1)## 对每个障碍进行分析for bi in new_barrier_dict:if new_barrier_dict[bi][0] in Neib_Dict: # 如果当前障碍位于点灯邻域内if new_barrier_dict[bi][3] != 0: # 如果不等于0，则将所需灯数减1new_barrier_dict[bi][3] = new_barrier_dict[bi][3] - 1else:# 如果等于0，说明当前方案又去return False, {}return True,new_barrier_dict## 这里设置一个程序，将灯所在行列全部赋值-20（被遮挡的区域除外）def Render(self,ni_rr, ni_cc,Data):# 填充所在行和所在列的元素new_Data = []for rr in range(len(Data)):temp = []for cc in range(len(Data[0])):temp.append(Data[rr][cc])new_Data.append(temp)##1 查找当前行是否存在阻碍Cs_little = [0]Cs_large = [math.inf]for bi in self.barrier_keys:  # 与障碍区域进行比较bi_r, bi_c = map(int,bi.split(';'))#Barrier_dict[bi][1], Barrier_dict[bi][2]if bi_r == ni_rr:if ni_cc>bi_c:Cs_little.append(bi_c+1)else:Cs_large.append(bi_c-1)start_c = max(0,max(Cs_little))end_c = min(CC-1,min(Cs_large))for ic in range(CC):if start_c<=ic<=end_c:new_Data[ni_rr][ic] = -20 #点亮之后，编程-20##2 查找当前列是否存在阻碍Rs_little = [0]Rs_large = [math.inf]for bi in self.barrier_keys:  # 与障碍区域进行比较bi_r, bi_c = map(int, bi.split(';'))  # Barrier_dict[bi][1], Barrier_dict[bi][2]# bi_r, bi_c = Barrier_dict[bi][1],Barrier_dict[bi][2]if bi_c == ni_cc:if ni_rr > bi_r:Rs_little.append(bi_r+1)else:Rs_large.append(bi_r-1)start_r = max(0, max(Rs_little))end_r = min(RR-1, min(Rs_large))for ir in range(RR):if start_r <= ir <= end_r:new_Data[ir][ni_cc] = -20  # 点亮之后，编程-20## 特别地new_Data[ni_rr][ni_cc] = -30 #点灯的位置用-30表示return new_Data# # 判断当前行列中，是否存在已点亮的灯，def D_ErrorL(self,ni_rr, ni_cc, new_lamps):Error_lams = []# 特殊情况，此时不存在点灯冲突if len(new_lamps) == 0:return Error_lamselse:# 检测是否存在点灯冲突for lamp in new_lamps: # 对于已经点灯的点进行分析l_r,l_c = map(int,lamp.split(';'))# 对于同一行而言，判断两者之间是否有障碍if ni_rr == l_r:Flag_r = False # 用于标记两者之间是否有阻碍for bi in self.barrier_keys:# 与障碍区域进行比较bi_r,bi_c = map(int,bi.split(';'))if bi_r == ni_rr:if min(ni_cc,l_c)<bi_c<max(ni_cc,l_c):# 说明没问题Flag_r = Truebreakif Flag_r == False: # 说明两者之间没有阻碍，有误Error_lams.append(str(l_r)+';'+str(l_c))# 对于同一列而言，判断两者之间是否有障碍if ni_cc == l_c:Flag_c = False  # 用于标记两者之间是否有阻碍for bi in self.barrier_keys:bi_r, bi_c = map(int, bi.split(';'))if bi_c == ni_cc:if min(ni_rr, l_r) < bi_r < max(ni_rr, l_r):# 说明没问题Flag_c = Truebreakif Flag_c == False:  # 说明两者之间没有阻碍，有误Error_lams.append(str(l_r)+';'+str(l_c))return Error_lams## 迎接输入
data_size = []
barrier_num = []
barrier_data = []
while True:##N,M = map(int,input().strip().split())if N==0 and M==0:breakelse:data_size.append([N,M])##temp_num = int(input().strip())barrier_num.append(temp_num)temp = []for ni in range(temp_num):temp.append(input().strip())barrier_data.append(temp)
# print(barrier_data)## 数据提取
case_num = len(data_size)
for case in range(case_num):#1 提取的数据RR,CC = data_size[case][0],data_size[case][1] # 数据矩阵的长宽B_num = barrier_num[case]B_data = barrier_data[case]#1.1 数据转化subData,Data_dict,Stop_dict,Barrier_dict = sub2Dict(RR,CC,B_num,B_data)# print(subData)# print(dict)## 接下来，需要设计方法进行dfs搜索了：查找所有可行的方案，并返回满足要求的最少灯数。test = Solution()ans = test.DFS()if ans < math.inf:print(ans)else:print("No solution")

输入：

2 2
0
2 2
1
2 2 1
6 7
7
2 3 -1
3 3 0
4 2 1
5 4 3
5 6 2
1 7 -1
6 5 -1
0 0

输出：

2
No solution
8