本文主要是介绍Andrew Ng机器学习--L6:逻辑回归,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
Lecture 6_Logistic Regression 逻辑回归
- 6.1 分类问题 Classification
- 6.2 假设表示 Hypothesis Representation
- 6.3 决策边界 Decision Boundary
- 6.4 代价函数 Cost Function
- 6.5 简化的代价函数和梯度下降 Simplified Cost Function and Gradient Descent
- 6.6 高级优化 Advanced Optimization
- 6.7 多类别分类:一对多 Multiclass Classification_ One-vs-all
- 相关术语
虽然逻辑回归名字里有一个回归,但它不是回归算法。而是一种非常强大,甚至可能世界上使用最广泛的一种分类算法。
特征缩放也适用于逻辑回归。
6.1 分类问题 Classificatio
6.1 分类问题 Classification
参考视频 p32
二值分类问题 binary classification problem 定义如下:

6.2 假设表示 Hypothesis Representation
参考视频 p33
引入一个新的模型:逻辑回归。该输出变量范围始终在 0和1 之间。 逻辑回归模型的假设是:
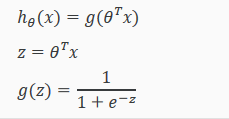
𝑋 代表特征向量;
𝑔 代表逻辑函数Logistic Function 也叫 Sigmoid Function,其曲线如下:
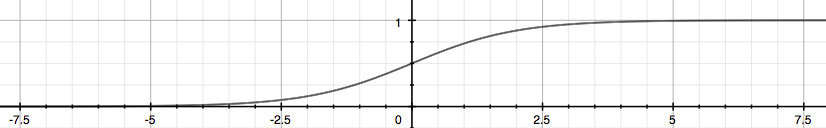
给定输入变量x,根据选择的参数Θ,h(x)给出 y=1 的概率。y=0 的概率是 1 - h(x)
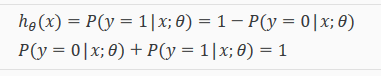
6.3 决策边界 Decision Boundary
参考视频 p34
决策边界就是模型中预测为1 和预测为0的区域的分界线。The decision boundary is the line that separates the area where y = 0 and where y = 1. It is created by our hypothesis function.

线性的决策边界:
非线性的决策边界:

6.4 代价函数 Cost Function
参考视频 p35
如果沿用线性回归里的代价函数,则会导致J(𝜃) 不是凸函数,引发很多局部最优解。

为了拟合逻辑回归模型的参数 𝜃,代价函数如下:
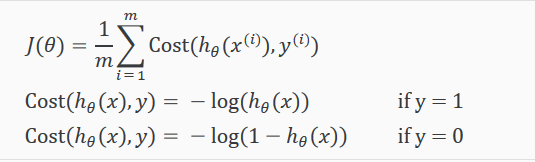
根据上面的公式计算代价,当预测和实际一致时代价为0,反之代价为无穷大。
y = 1时,h(x) 和 J(Θ) 对应曲线如下:

y = 0时, h(x) 和 J(Θ) 对应曲线如下:
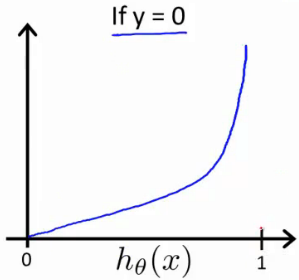
即有以下规律:
- Cost(hθ(x),y) = 0 if hθ(x)=y
- Cost(hθ(x),y)→∞ if y=0 and hθ(x)→1
- Cost(hθ(x),y)→∞ if y=1 and hθ(x)→0
6.5 简化的代价函数和梯度下降 Simplified Cost Function and Gradient Descent
参考视频 p36
将上面两个式子 简化为下面一个式子(当 y 分别等于0或1时,式子只剩下两项中的一项):
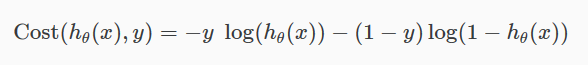
完整的代价函数如下:
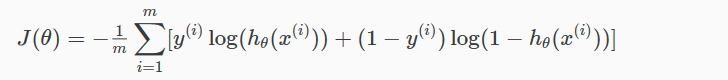
一个向量实现如下:
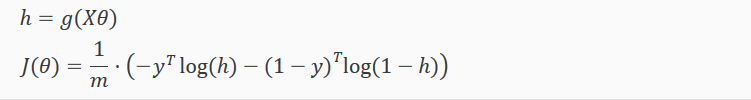
梯度下降过程如下:

使用数学方法推倒上式中 J(Θ) 的导数:

带入更新算法中,得到下面算法:
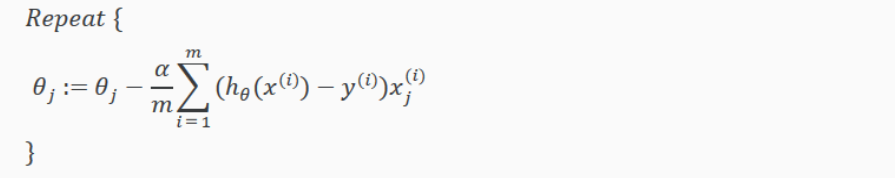
上面这个梯度下降算法 看起来和线性回归一样,但事实上是完全不同的。因为之前 h(x) 是线性函数,而逻辑回归中 h(x) 定义如下:
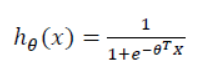
一个梯度下降的向量化实现如下
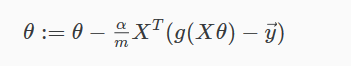
6.6 高级优化 Advanced Optimization
参考视频 p37
除梯度下降算法以外,还有一些常被用来令代价函数最小的算法。这些算法更加复杂和优越,而且通常不需要人工选择学习率,比梯度下降算法要更加快速。这些有: 共轭梯度 (Conjugate Gradient), 局部优化法 (Broyden fletcher goldfarb shann,BFGS)和有限内存局部优化法 (LBFGS)。
这些算法有一个智能的内部循环,称为线性搜索(line search)算法,它可以自动尝试不同的学习速率 。只需要给这些算法提供计算导数项和代价函数的方法,就可以返回结果。适用于大型机器学习问题。
它们太复杂,不应该自己实现,而是调用MATLAB方法。例如一个无约束最小值函数 fminunc 。它会使用众多高级优化算法中的一个,就像加强版的梯度下降法,自动选择学习速率,找到最佳的 Θ 值。
使用时需要提供代价函数和每个参数的求导,我们自己实现 costFunction 函数,传入参数Θ,可以一次性返回以下两个值:
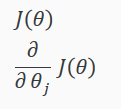
例子,调用 fminunc() 函数,用@传入costFunction函数的指针,初始化的 theta,还可以增加 options(GradObj = on 指 “打开梯度目标参数”,即我们会给这个函数提供梯度参数):

6.7 多类别分类:一对多 Multiclass Classification_ One-vs-all
参考视频 p38
多分类问题中,y 有 {0,1…n} 一共 n+1 中可能值。方法:
(1)拆分成 n+1 个二分类问题。
(2)对每个分类,都预测出一个h(x)值。代表 y是这个类型的可能性。
(3)最后结果为可能性最大的那个类型。


相关术语
decision boundary 决策边界
loophole 漏洞
nonlinear 非线性
penalize 使不利
这篇关于Andrew Ng机器学习--L6:逻辑回归的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!









