数学建模基础学习笔记（乱记）

一、层次分析法（AHP）

• The analytic hierarchy process (简称：AHP）
• 主要应用于解决评价类问题（比如选哪种方案比较好，哪种运动员或者员工表现地更优秀等）

1、权重打分方案引入

• 我们面临毕业，打算直接就业，你参加了EY和阿里的秋招面试，并成功都拿到了offer，现在，你需要去选择，你的最终职业去向，这时，我们就要对我们的目标选择对象进行评估。
• 而不同的人对于职业不同方面的倾向性不同，所以我们要对不同的部分进行加权，也就是定一下我们的指标。
• 比如分为：
  • 公司环境（0.3）
  • 地理位置（0.2）
  • 职业发展路径（0.3）
  • 公司福利（0.2）（括号里的权重其实就是不同部分的重要程度，权重之和为1）
• 这样对于不同的指标我们就有了不同的权重，对于我们接下来的评分做了基础性工作。
  

二、评价类问题

• 对于评价类问题，我们要先去思考三个问题：
  • 1、我们评价的目标是什么？
  • 2、我们为了达到这个目标有哪几种可选的方案？
  • 3、评价的准则（指标）是什么？（评价的依据）（需要我们自行搜索论文、知乎等找到相关的思路）

层次分析法

• 要想获得较为科学的分值，我们需要进行两两比较
  
• 假设我们有n个指标，我们则需要进行两两比较，需要组合数（n，2）次两两比较
• 我们将所得的标度列成矩阵：
  

一致矩阵

• 满足：
  
• 对于一致矩阵，有这样的特点：各行各列之间成倍数关系
  

一致性检验

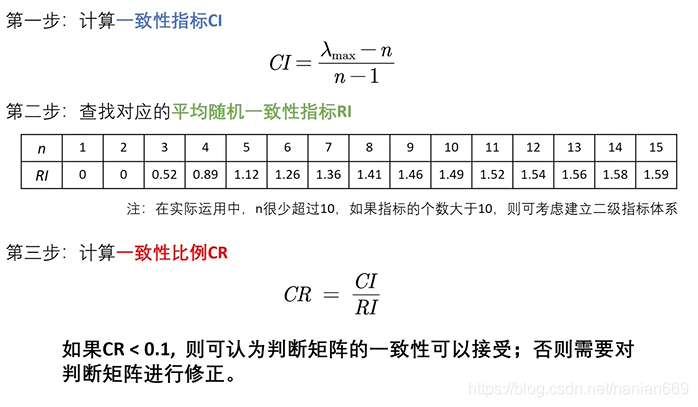
权重的求解

归一化

（1）一致矩阵情况

• 我们只需要任取一列，将我们所要求解的项的值除以全列之和就可以了（取得的数即权重）

（2）判断矩阵情况

• 依然用如上方法，求出每列的数据，然后取平均
• 将归一化的各列相加（按行求和）
• 将相加后所得向量中的每一个元素除以n即可获得权重向量
  

特征值法求权重

层次分析法图解

（三）总结

• 层次分析法( The Analytic Hierarchy Processa即AHP)是由美国运筹学家、匹兹堡大学教授T.L. Saaty于20世纪70年代创立的一种系统分析与决策的综合评价方法，是在充分研究了人类思维过程的基础上提出来的，它较合理地解决了定性问题定量化的处理过程。
• AHP的主要特点是通过建立递阶层次结构，把人类的判断转化到若干因素两两之间重要度的比较上，从而把难于量化的定性判断转化为可操作的重要度的比较上面。在许多情况下，决策者可以直接使用AHP进行决策，极大地提高了决策的有效性、可靠性和可行性，但其本质是一种思维方式，它把复杂问题分解成多个组成因素，又将这些因素按支配关系分别形成递阶层次结构，通过两两比较的方法确定决策方案相对重要度的总排序。整个过程体现了人类决策思维的基本特征，即分解、判断、综合，克服了其他方法回避决策者主观判断的缺点。
  
  清风老师的建议，给力

二、TOPSIS法

• TOPSIS法（Technique for Order Preference by Similarity to Ideal Solution），可以译为逼近理想解排序法，国内通常称为优劣解距离法
• 它是一种常用的综合评价方法，能充分地利用原始信息，其结果可以精确地反映方案之间地差距

（一）引入

• 我们可以构造一种评分方法：
  
• 在评价的时候，我们要注意，对于 越大越好 的指标****，我们称其为极大型指标（效益性指标），对于 越小越好 的指标，我们称其为极小型指标（成本型指标）

1、指标正向化

• 这时候，为了方便比较，我们要将指标类型进行统一，最常用的方法：就是将所有的指标转化为极大型，我们称其为指标正向化。
• 极小化指标类型转化为极大型指标类型：max - x

2、标准化处理

• 为了消除不同指标量纲的影响，我们需要对已经正向化的矩阵进行标准化处理
  

3、归一化

3、常见的四种指标

（1）中间型指标转化

• 中间型指标，其实就是对应一个最优值，我们的每一个样本数值和最优值差值越小即越好，其本质上可以看作是极小型指标

（2）区间型指标转化

4、扩展

• 加权的TOPSIS法