本文主要是介绍GRAPH ATTENTION NETWORKS 论文/GAT学习笔记,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
背景
目标:适用不同结构的图的模型
图卷积
- 基于谱的方法 :
- 这些方法学习得到的filters基于拉普拉斯特征基,而拉普拉斯特征基又基于图结构,所以在特定结构上训练的模型不能直接应用到具有不同结构的图。
- 代表:GCN
- 不基于谱的方法 :
- 直接在图上定义卷积 (对空间上近邻的群体使用),但是很难定义能够同时作用于不同数量领域并且保持CNNs权重共享特性的方法
- 代表:graphsage
注意力机制:可以处理可变大小的输入,专注于输入中最相关的部分来做出决定
- 可以跨节点邻居对并行计算,非常高效
- 可以通过为邻居指定任意权重来适用于具有不同度的图节点
- 适用于inductive学习方法
所以作者提出了基于注意力机制的方法来完成节点分类任务。其基本思想为:通过关注节点的邻居并遵循self-attention策略来计算图中每个节点的隐藏表征。
GAT架构
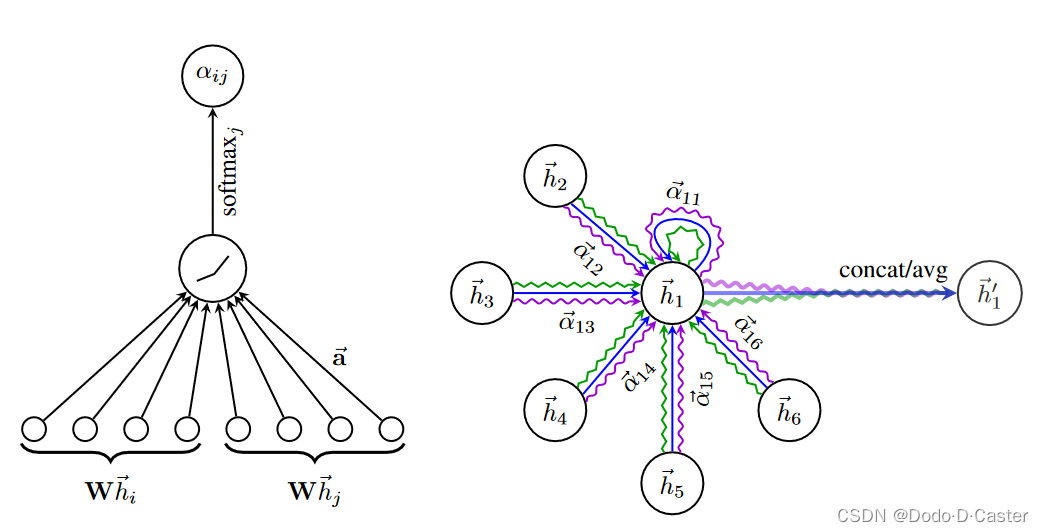
输入: h = { h 1 ⃗ , h 2 ⃗ , . . . , h N ⃗ } , h i ⃗ ∈ R F h = \{ \vec{h_1}, \vec{h_2}, ..., \vec{h_N} \}, \vec{h_i} \in \R ^F h={h1,h2,...,hN},hi∈RF
输出: h ′ = { h 1 ′ ⃗ , h 2 ′ ⃗ , . . . , h N ′ ⃗ } , h i ′ ⃗ ∈ R F ′ h' = \{ \vec{h_1'}, \vec{h_2'}, ..., \vec{h_N'} \}, \vec{h_i'} \in \R ^{F'} h′={h1′,h2′,...,hN′},hi′∈RF′
- N :节点数
- F :节点特征数
注意力系数 (attention coefficients) 代表节点 j 的特征对节点 i 的重要程度,其计算公式为:
e i j = a ( W h i ⃗ , W h j ⃗ ) e_{ij} = a (W \vec{h_i}, W \vec{h_j} ) eij=a(Whi,Whj)
- a : 一个共享的注意力机制 R F ′ × R F ′ → R \R ^{F'} \times \R ^{F'} \rightarrow \R RF′×RF′→R
- W : 权重矩阵 W ∈ R F ′ × F W \in \R ^{F' \times F} W∈RF′×F
标准化注意力系数:
α i j = s o f t m a x j ( e i j ) = e x p ( e i j ) ∑ k ∈ N i e x p ( e i k ) \alpha _{ij} = softmax_j(e_{ij})=\frac{exp(e_{ij})}{\sum _{k \in \mathcal{N} _i} exp(e_{ik}) } αij=softmaxj(eij)=∑k∈Niexp(eik)exp(eij)
计算下一层特征:
h ⃗ i ′ = σ ( ∑ j ∈ N i α i j W h ⃗ j ) \vec{h}_i' = \sigma (\sum_{j\in \mathcal{N}_i} \alpha _{ij} W \vec{h}_j ) hi′=σ(j∈Ni∑αijWhj)
使用multi-head attention来让学习过程更稳定:
h ⃗ i ′ = ∥ k = 1 K σ ( ∑ j ∈ N i α i j k W k h ⃗ j ) \vec{h}_i' = \parallel _{k=1}^K \sigma (\sum_{j\in \mathcal{N}_i} \alpha _{ij}^k W ^k\vec{h}_j ) hi′=∥k=1Kσ(j∈Ni∑αijkWkhj)
- ∣ ∣ || ∣∣ : 表示连接操作
- α i j k \alpha _{ij}^k αijk : 表示由第k个注意力机制 a k a^k ak 计算的标准化注意力机制系数
- W k W^k Wk : 相应输入线性变化的权重矩阵
- h ′ h' h′ 会有 K F ′ K F' KF′ 个特征,而不是 F ′ F' F′ 个
在最终层 (预测层),连接操作就不再有意义,作者采用了平均的方法,同时将非线性激活函数放在了外面。
h ⃗ i ′ = σ ( 1 K ∑ k = 1 K ∑ j ∈ N i α i j k W k h ⃗ j ) \vec{h}_i' = \sigma ( \frac{1}{K} \sum _{k=1}^K \sum_{j\in \mathcal{N}_i} \alpha _{ij}^k W ^k\vec{h}_j ) hi′=σ(K1k=1∑Kj∈Ni∑αijkWkhj)
本文的设置
本文的实验中,注意力机制 a 是一个单层前反馈神经网络
- 由权重向量 a ⃗ ∈ R 2 F ′ \vec{a} \in \R ^{2F'} a∈R2F′参数化
- 采用LeakyReLU非线性 (negative input slope α = 0.2 \alpha = 0.2 α=0.2)
并且只计算节点 i 自身及其一阶邻居的注意力系数,表达式为:
e i j = a ( W h i ⃗ , W h j ⃗ ) = L e a k y R e L U ( a ⃗ T [ W h i ⃗ ∣ ∣ W h j ⃗ ] ) e_{ij} = a (W \vec{h_i}, W \vec{h_j} ) = LeakyReLU(\vec{a}^T [W \vec{h_i} || W \vec{h_j}] ) eij=a(Whi,Whj)=LeakyReLU(aT[Whi∣∣Whj])
总的公式表示为:
α i j = e x p ( L e a k y R e L U ( a ⃗ T [ W h i ⃗ ∣ ∣ W h j ⃗ ] ) ) ∑ k ∈ N i e x p ( L e a k y R e L U ( a ⃗ T [ W h i ⃗ ∣ ∣ W h k ⃗ ] ) ) \alpha _{ij} = \frac{exp(LeakyReLU(\vec{a}^T [W \vec{h_i} || W \vec{h_j}] ))}{\sum _{k \in \mathcal{N} _i} exp(LeakyReLU(\vec{a}^T [W \vec{h_i} || W \vec{h_k}] )) } αij=∑k∈Niexp(LeakyReLU(aT[Whi∣∣Whk]))exp(LeakyReLU(aT[Whi∣∣Whj]))
- ⋅ T \cdot ^T ⋅T : 表示转置
- ∣ ∣ || ∣∣ : 表示连接操作
GAT vs 其他方法
优点
- 计算高效:self-attentional 层的计算可以在所有边上并行,输出特征的计算可以在所有节点上并行,同时不需要高复杂度的矩阵运算
- 相比GCN,GAT可以为相同的邻域中的节点赋不同的权重,实现了模型容量的飞跃,并且更具可解释性。
- 注意力机制以共享的方式应用于图中所有的边,所以不用预先知道全图结构或者所有节点的特征
- graphsage采样了固定数目的邻居,而GAT则作用于整个邻域,也不需要处理节点的顺序(graphsage采用LSTM作为聚合器需要随机邻居顺序)
- GAT是MoNet的一个特例,但是使用节点特征而不是节点的结构属性来进行相似性计算,从而保证了GAT不需要预先知道图的结构
缺点
- 采用稀疏矩阵,但框架只支持2阶张量的稀疏矩阵乘法,限制了batch的处理能力
- 由于图结构没有规律,使用GPU无法带来性能提升
- 可接受域的大小受到网络深度的限制 (和GCN及类似模型一样)
- 由于邻域会在图中高度重叠,并行计算会带来大量冗余计算
实验
数据集:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-wJjMpDyC-1672227079416)(https://s3-us-west-2.amazonaws.com/secure.notion-static.com/e5dfd7d3-9511-434a-9922-fdf3e5978451/Untitled.png)]
实验设置
- transductive (两层):
- 第一层用于降维 (从64维feature降到8维),K=8 个 attention head,激活函数为ELU
- 第二层用于分类,单个 attention head 计算 C 维特征 (C为类别数),激活函数为softmax
- inductive (两层):
- 前两层用于降维 (1024 features → 256 features),都有 K=4 个 attention head,激活函数为ELU
- 第三层用于分类 (121 features),K=6 个 attention head,激活函数为 logistic sigmoid
结果:
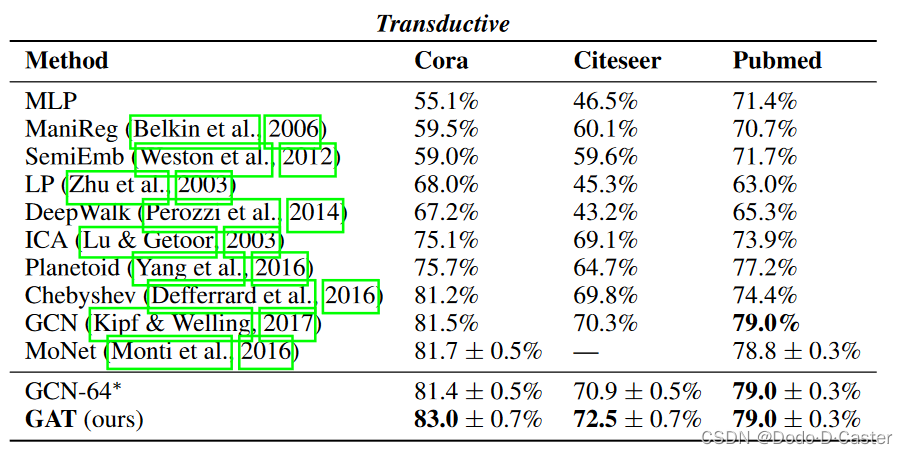
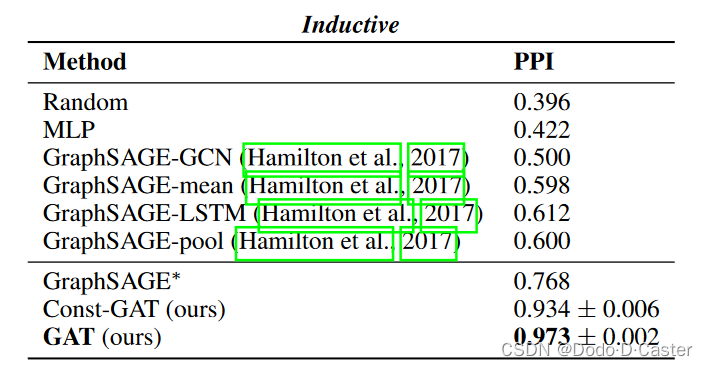
这篇关于GRAPH ATTENTION NETWORKS 论文/GAT学习笔记的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







