原文链接:https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.100.114101
发表在:PRL 2008
--------------------------------------------------------------------------------------------------------------------------------------------------------------------
传统的模型的coupling的形式,
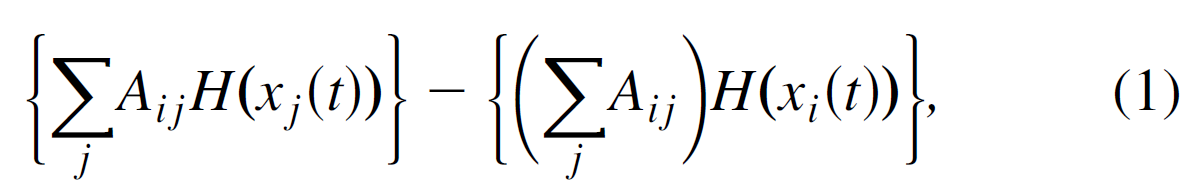
其中,Aij 代表j到i的coupling强度,Aii=0, xi(t)是对应节点i的n维状态变量,H:Rn --> Rn, 一共有N个节点。
假设:对于节点i,
a. (1)式的第一项是可观测的信号,定义该信号为,
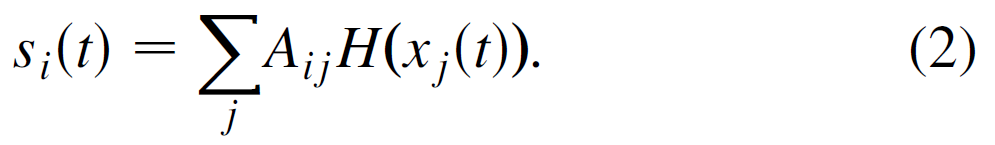 b. 不知道输入的强度和,i.e., ∑j Aij.
b. 不知道输入的强度和,i.e., ∑j Aij.
接下来考虑下面的形式,
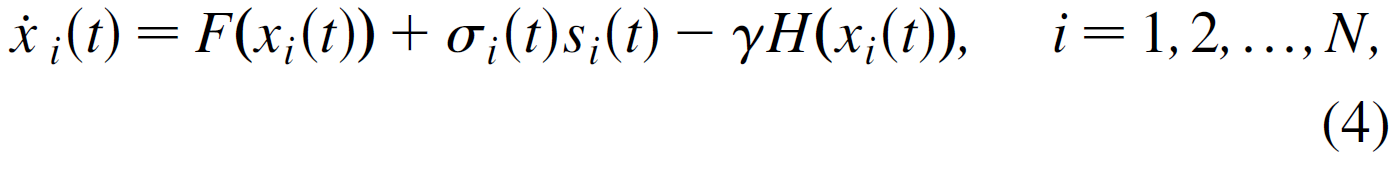
γ:constan gain 对于所有的节点. 同步解,
![]()
存在, 当σi(t) 等于
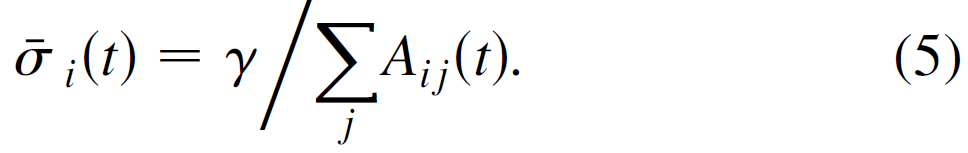
注意到,当

式子(4)可以写成,

其中

并且行和都等于0. 如果存在同步解,那么(7)式的最后一项就恒等于0. 动力学方程就变成了没有coulping的形式,
![]()
在这种情况下,根据master stability function theory, 同步解的稳定性可以通过选取合适的couping γ 保证.
需要注意的是,如果σi(t) 不满足(5)式,就不能保证同步解的稳定性了。下面将试着去如何设计σi(t) , 并且我们事先假设选取的 γ 能够使得同步解在σi(t) 满足(5)式时是稳定的。
在给出具体σi(t)的设计之前,对于节点i,我们先定义一个量,
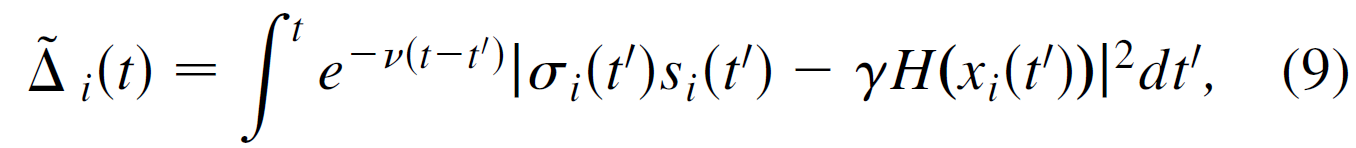
并且选择ν满足,
![]()
其中τS和τN分别是节点动力系统xi(t)的time scale,网络结构Aij(t)的time scale. 有了上面的这个假设,(9)式中σi(t') 就可以用σi(t) 代替(我没怎么看出来。。),从而近似(9)式,得到,
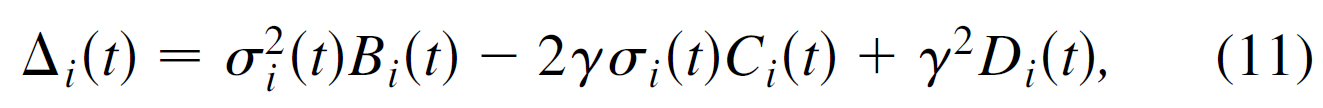
其中
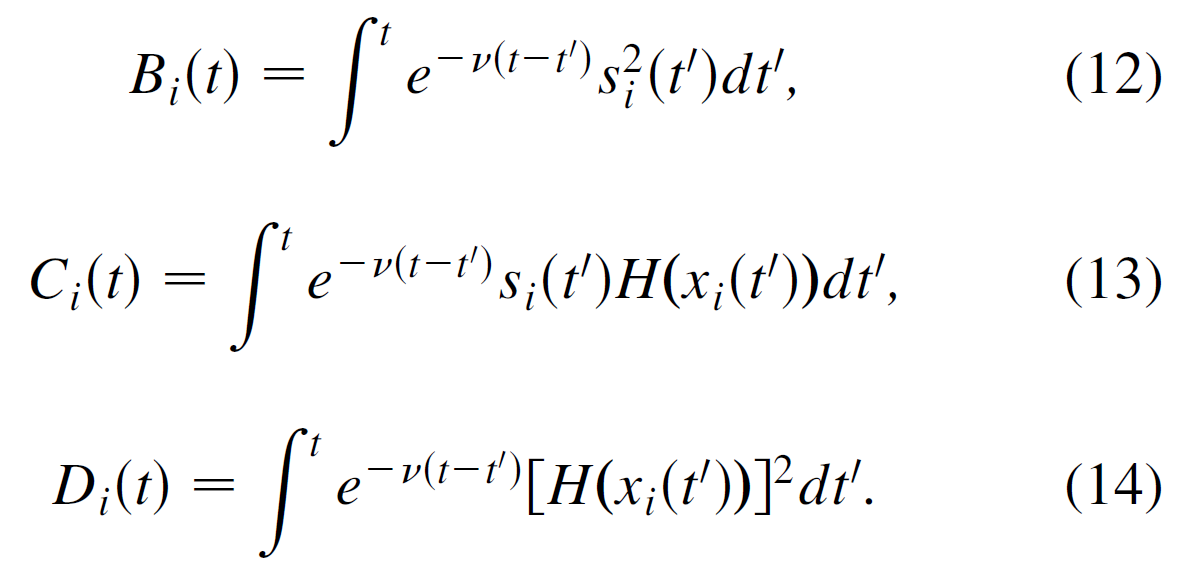
对于(9)式,如果等于0,那么就是同步,所以可以通过梯度下降的方法求近似解Δi的最小值,即,
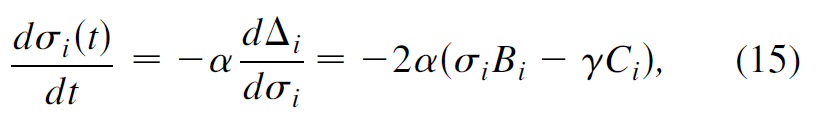
其中α是可调参数。 未来避免(12)和(13)式算积分,将其写成ODE的形式如下,

综上,设计的adaptive 策略可以用一组微分方程表示,i.e., 式子(4),(11),(15),(16).
实验
考虑一个N个节点的随机网络,<k>N/2 条无向边,<k>是平均度。对于t=0时候,如果节点i和节点j有边,那么邻接矩阵Aij(0)=Aji(0)=1,否则Aij(0)=0. 当t>0的时候,假设网络的演化为,
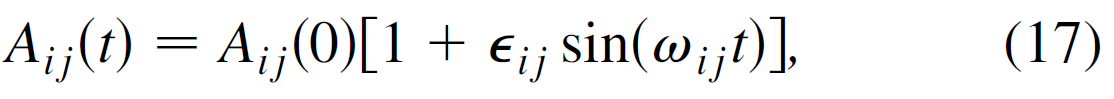
εij是[0, 1]的随机数,ωij是[ωmin, ωmax]之间的随机数,ωmax > ωmin > 0 . 并且网络的时间尺度τN=(ωmax )-1, much longer than 节点动力学的时间尺度τS,i.e., τN>τS,
考虑Rossler oscillators,
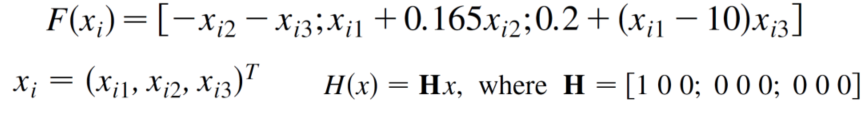
为了简单起见,假设自适应过程(15)非常快. 让α→oo, 那么 σi(t) 快速收敛到γCi(t)/Bi(t). 这样子,我们可以之间把(11)式子替换成,

v以及Ci,Bi的初值对动力学是至关重要的。假设Aij(0)是已知的,我们让Ci(0)=Bi(0)×[ΣjAij(0)]-1, 从而能够在初始时刻满足式子(6).
因为耦合系统可能存在其它的吸引子,我们希望设计合适的初值Bij(0),使得一开始耦合系统就落在同步解的吸引域中。为此,我们假设已经在同步解(8)上了,对式子(16)在时间轴上取平均,得到近似,Bi ≈ <si2>, 根据这个例子H(x)=(x, 0, 0)T, 我们有<si2>≈<k2><xS12>t, 其中<xS12>t是同步解(8)xS1(t)在时间轴上的平均, 即,
![]()
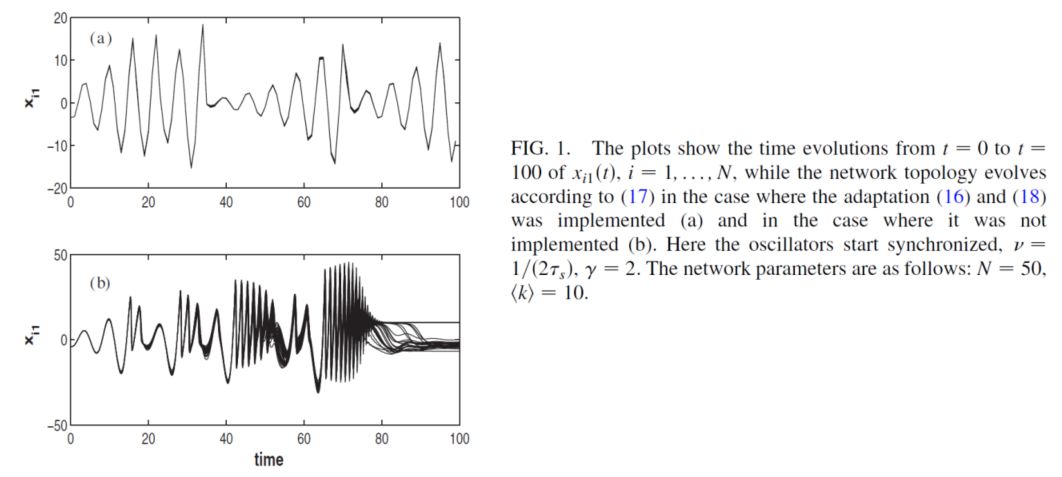
下面是数值结果,Figure 1(a)显示的是adaption ((16)和(18),(17))的结果,几乎50个节点的演化轨迹都是一样的(几乎重合了) . Fig. 1(b)是没有adaption的结果, i.e.,