论文阅读：Representation Learning with Contrastive Predictive Coding

Representation Learning with Contrastive Predictive Coding

• 参考一些NLP方法
• 理解Contrastive Learning

CPC

Motivation: 该论文认为，随着预测未来更多的帧，一些noisy的低层信息会被忽略掉，更多的共享信息(该论文称之为slow features)会被提取到，这也是一些更应被关注的信息。论文举了几个例子:phonemes,object,story line.

去真正的预测未来帧并不是一件简单且必要的事情，因此论文提出学习到某种可以使得当前状态c和未来帧x之间互信息最大的表示。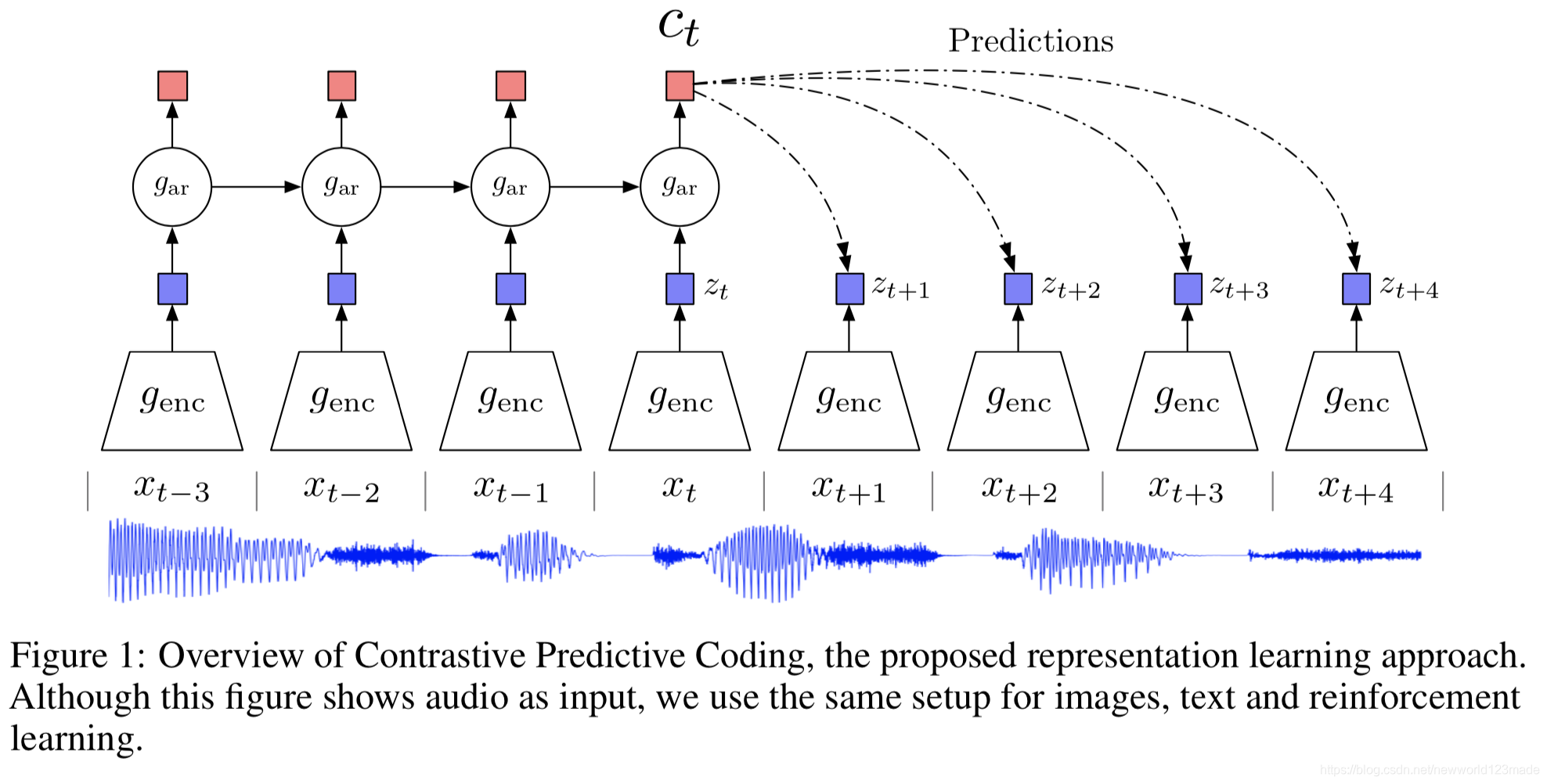
MI表示：
$$I(x,c)=H(x)-H(x|c)=\sum _{x,c}p(x,c)log\frac{p(x|c)}{p(x)}$$
论文中要以某种loss函数的形式来最大化当前编码$c_t$与未来帧$x_{t+k}$之间的互信息。
而上述MI公式中的$\frac{p(x|c)}{p(x)}$不容易计算。CPC给出的解决方案是利用最大化所提出的InfoNCE loss来最大化MI的一个下界。

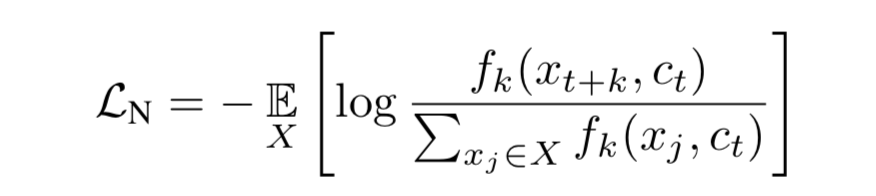
如上述，给定 X = { x 1 , x 2 , . . . , x N } X=\{x_1, x_2, ..., x_N\} X={x1​,x2​,...,xN​}其中$x_n(n\ne i)$采样自p(x), 而$x_i$采样于$p(x_{t+k}|c_t)$. 实际上当前的X中postive是$x_i$的概率
$$\begin{gathered} p(d=i|X,c_t)=\frac{p(d=i,X|c_t)}{p(X|c_t)} \\ =\frac{p(d=i,X|c_t)}{{\sum }_{j}p(d=j,X|c_t)} \\ =\frac{p(x_1|c_t)p(x_2|c_t)...p(x_i|c_t)...p(x_N|c_t)}{{\sum }_{j}p(x_1|c_t)p(x_2|c_t)...p(x_j|c_t)...p(x_N|c_t)} \\ =\frac{p(x_1)p(x_2)..p(x_i|c_t)...p(x_N)}{{\sum }_{j}p(x_1)p(x_2)...p(x_j|c_t)...p(x_N)} \\ =\frac{\frac{p(x_i|c_t)}{p(x_i)}}{{\sum }_j\frac{p(x_j|c_t)}{p(x_j)}} \end{gathered}$$

所以$$f_k(x_{t+k},c_t)$$正比于上述分子。

但是为何${\mathcal{L}}_N$中的分式代表$p(d=i|X,c_t)$，论文中大致是这样描述的：
$\frac{f_k(x_{t+k},c_t)}{{\sum }_x{f}_k(x,c_t)}$是一个正样本类别概率，当优化${\mathcal{L}}_N$的时候，就是在最大化这个正样本类别概率，其实类似于一个最大似然估计的过程，来估计出上述的$p(d=i|X,c_t)$

在理论上的解释就是上面的内容，技术上，其实这类往往比较容易实现，道理也很直观。

由于$f$只是一个由参数决定的估计值，$f$被feed $x_i,c_t$和负样本$x_j,c_t$，计算softmax分类即可，直观上可以认为是一种contrastive loss, 即配对的当前状态$c_t$和未来帧$x_{t+k}$通过$f$后的值较大，而不配对的较小。实际上就是给你一堆$x$,网络有能力判断出与$c_t$匹配的哪个$x_i$.

其实这类论文的思路按照theory->method的顺序往往难以理解，但是按照method->theory的顺序往往是容易的，即随便想一个intuitive的loss，将其想法设法与已有的统计量发生关联，给出一个合理的数学解释。

CPC的实验部分：