傅立叶变化，小波变换，滤波

傅立叶变化：
傅立叶变换是一种线性的积分变换，常在将信号在时域（或空域）和频域之间变换时使用，在物理学和工程学中有许多应用。因其基本思想首先由法国学者约瑟夫·傅里叶系统地提出，所以以其名字来命名以示纪念。在不同的研究领域，傅立叶变换具有多种不同的变体形式，如连续傅立叶变换和离散傅立叶变换。最初傅立叶分析是作为热过程的解析分析的工具被提出的。
傅立叶变换，表示能将满足一定条件的某个函数表示成三角函数（正弦和/或余弦函数）或者它们的积分的线性组合。在不同的研究领域，傅立叶变换具有多种不同的变体形式，如连续傅立叶变换和离散傅立叶变换。最初傅立叶分析是作为热过程的解析分析的工具被提出的。
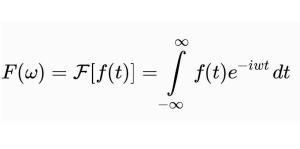小波变换 （Wavelet transform）：
小波变换（wavelet transform，WT）是一种新的变换分析方法，它继承和发展了短时傅立叶变换局部化的思想，同时又克服了窗口大小不随频率变化等缺点，能够提供一个随频率改变的“时间-频率”窗口，是进行信号时频分析和处理的理想工具。它的主要特点是通过变换能够充分突出问题某些方面的特征，能对时间（空间）频率的局部化分析，通过伸缩平移运算对信号（函数)逐步进行多尺度细化，最终达到高频处时间细分，低频处频率细分，能自动适应时频信号分析的要求，从而可聚焦到信号的任意细节，解决了Fourier变换的困难问题，成为继Fourier变换以来在科学方法上的重大突破。
传统的信号理论，是建立在Fourier分析基础上的，而Fourier变换作为一种全局性的变化，其有一定的局限性，如不具备局部化分析能力、不能分析非平稳信号等。在实际应用中人们开始对Fourier变换进行各种改进，以改善这种局限性，如STFT（短时傅立叶变换）。由于STFT采用的的滑动窗函数一经选定就固定不变，故决定了其时频分辨率固定不变，不具备自适应能力，而小波分析很好的解决了这个问题。小波分析是一种新兴的数学分支，它是泛函数、Fourier分析、调和分析、数值分析的最完美的结晶；在应用领域，特别是在信号处理、图像处理、语音处理以及众多非线性科学领域，它被认为是继Fourier分析之后的又一有效的时频分析方法。小波变换与Fourier变换相比，是一个时间和频域的局域变换因而能有效地从信号中提取信息，通过伸缩和平移等运算功能对函数或信号进行多尺度细化分析（Multiscale Analysis），解决了Fourier变换不能解决的许多困难问题。
小波分析
与Fourier变换相比，小波变换是空间（时间）和频率的局部变换，因而能有效地从信号中提取信息。通过伸缩和平移等运算功能可对函数或信号进行多尺度的细化分析，解决了Fourier变换不能解决的许多困难问题。小波变换联系了应用数学、物理学、计算机科学、信号与信息处理、图像处理、地震勘探等多个学科。数学家认为，小波分析是一个新的数学分支，它是泛函分析、Fourier分析、样条分析、数值分析的完美结晶；信号和信息处理专家认为，小波分析是时间—尺度分析和多分辨分析的一种新技术，它在信号分析、语音合成、图像识别、计算机视觉、数据压缩、地震勘探、大气与海洋波分析等方面的研究都取得了有科学意义和应用价值的成果。信号分析的主要目的是寻找一种简单有效的信号变换方法，使信号所包含的重要信息能显现出来。小波分析属于信号时频分析的一种，在小波分析出现之前，傅立叶变换是信号处理领域应用最广泛、效果最好的一种分析手段。傅立叶变换是时域到频域互相转化的工具，从物理意义上讲，傅立叶变换的实质是把这个波形分解成不同频率的正弦波的叠加和。正是傅立叶变换的这种重要的物理意义，决定了傅立叶变换在信号分析和信号处理中的独特地位。傅立叶变换用在两个方向上都无限伸展的正弦曲线波作为正交基函数，把周期函数展成傅立叶级数，把非周期函数展成傅立叶积分，利用傅立叶变换对函数作频谱分析，反映了整个信号的时间频谱特性，较好地揭示了平稳信号的特征。
小波变换是一种新的变换分析方法，它继承和发展了短时傅立叶变换局部化的思想，同时又克服了窗口大小不随频率变化等缺点，能够提供一个随频率改变的“时间-频率”窗口，是进行信号时频分析和处理的理想工具。它的主要特点是通过变换能够充分突出问题某些方面的特征，因此，小波变换在许多领域都得到了成功的应用，特别是小波变换的离散数字算法已被广泛用于许多问题的变换研究中。从此，小波变换越来越引起人们的重视，其应用领域来越来越广泛。
应用
是与小波分析的理论研究紧密地结合在一起的。现在，它已经在科技信息产业领域取得了令人瞩目的成就。电子信息技术是六大高新技术中重要的一个领域，它的重要方面是图象和信号处理。现今，信号处理已经成为当代科学技术工作的重要部分，信号处理的目的就是：准确的分析、诊断、编码压缩和量化、快速传递或存储、精确地重构（或恢复）。从数学地角度来看，信号与图象处理可以统一看作是信号处理（图象可以看作是二维信号），小波分析的许多分析和应用问题，都可以归结为信号处理问题。现在，对于其性质随时间是稳定不变的信号（平稳随机过程），处理的理想工具仍然是傅立叶分析。但是在实际应用中的绝大多数信号是非稳定的（非平稳随机过程），而特别适用于非稳定信号的工具就是小波分析。
事实上小波分析的应用领域十分广泛，它包括：数学领域的许多学科；信号分析、图象处理；量子力学、理论物理；军事电子对抗与武器的智能化；计算机分类与识别；音乐与语言的人工合成；医学成像与诊断；地震勘探数据处理；大型机械的故障诊断等方面；例如，在数学方面，它已用于数值分析、构造快速数值方法、曲线曲面构造、微分方程求解、控制论等。在信号分析方面的滤波、去噪声、压缩、传递等。在图象处理方面的图象压缩、分类、识别与诊断，去污等。在医学成像方面的减少B超、CT、核磁共振成像的时间，提高分辨率等。
⑴小波分析用于信号与图象压缩是小波分析应用的一个重要方面。它的特点是压缩比高，压缩速度快，压缩后能保持信号与图象的特征不变，且在传递中可以抗干扰。基于小波分析的压缩方法很多，比较成功的有小波包最好基方法，小波域纹理模型方法，小波变换零树压缩，小波变换向量压缩等。
⑵小波在信号分析中的应用也十分广泛。它可以用于边界的处理与滤波、时频分析、信噪分离与提取弱信号、求分形指数、信号的识别与诊断以及多尺度边缘检测等。
⑶在工程技术等方面的应用。包括计算机视觉、计算机图形学、曲线设计、湍流、远程宇宙的研究与生物医学方面。
从图像处理的角度看，小波变换存在以下几个优点：
⑴小波分解可以覆盖整个频域（提供了一个数学上完备的描述）
⑵小波变换通过选取合适的滤波器，可以极大的减小或去除所提取得不同特征之间的相关性
⑶小波变换具有“变焦”特性，在低频段可用高频率分辨率和低时间分辨率（宽分析窗口），在高频段，可用低频率分辨率和高时间分辨率（窄分析窗口）
⑷小波变换实现上有快速算法（Mallat小波分解算法）