支持向量机 Part 1：完全线性可分下的支持向量分类与python实现—

本文主要是介绍支持向量机 Part 1：完全线性可分下的支持向量分类与python实现——机器学习笔记，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

* * * The Machine Learning Noting Series * * *

1. 概述：支持向量分类

支持向量机（Support Vector Machine, SVM）是在统计学习理论上发展起来的一种机器学习方法，在解决小样本、非线性和高维的分类、回归预测问题上有很多优势。

支持向量机分为支持向量分类机和支持向量回归机，分别用于输入变量和二分类/数值型输出变量间的数量关系和分类预测，简称支持向量分类（Support Vector Classification, SVC）；同理，支持向量回归（Support Vector Regression, SVR）用于输入变量和输出变量间的数量关系和回归预测。

支持向量分类主要有2情况：①完全线性可分样本指两类样本不重合，能被超平面百分百完全分开；而广义线性可分则找不到一个超平面完全将其分开；② 线性不可分样本找不到一个超平面将其线性分开，只能使用曲面，此类型的支持向量分类是支持向量机的灵魂，通过核函数解决。

2. 原理：完全线性可分下的支持向量分类

分类预测时，将训练集中的N个样本看成p维输入变量空间中的N个点（以点的不同形状或颜色代表输出变量的不同类别取值）。支持向量分类的目的是在p维空间中找到能将两类样本有效分开的超平面。

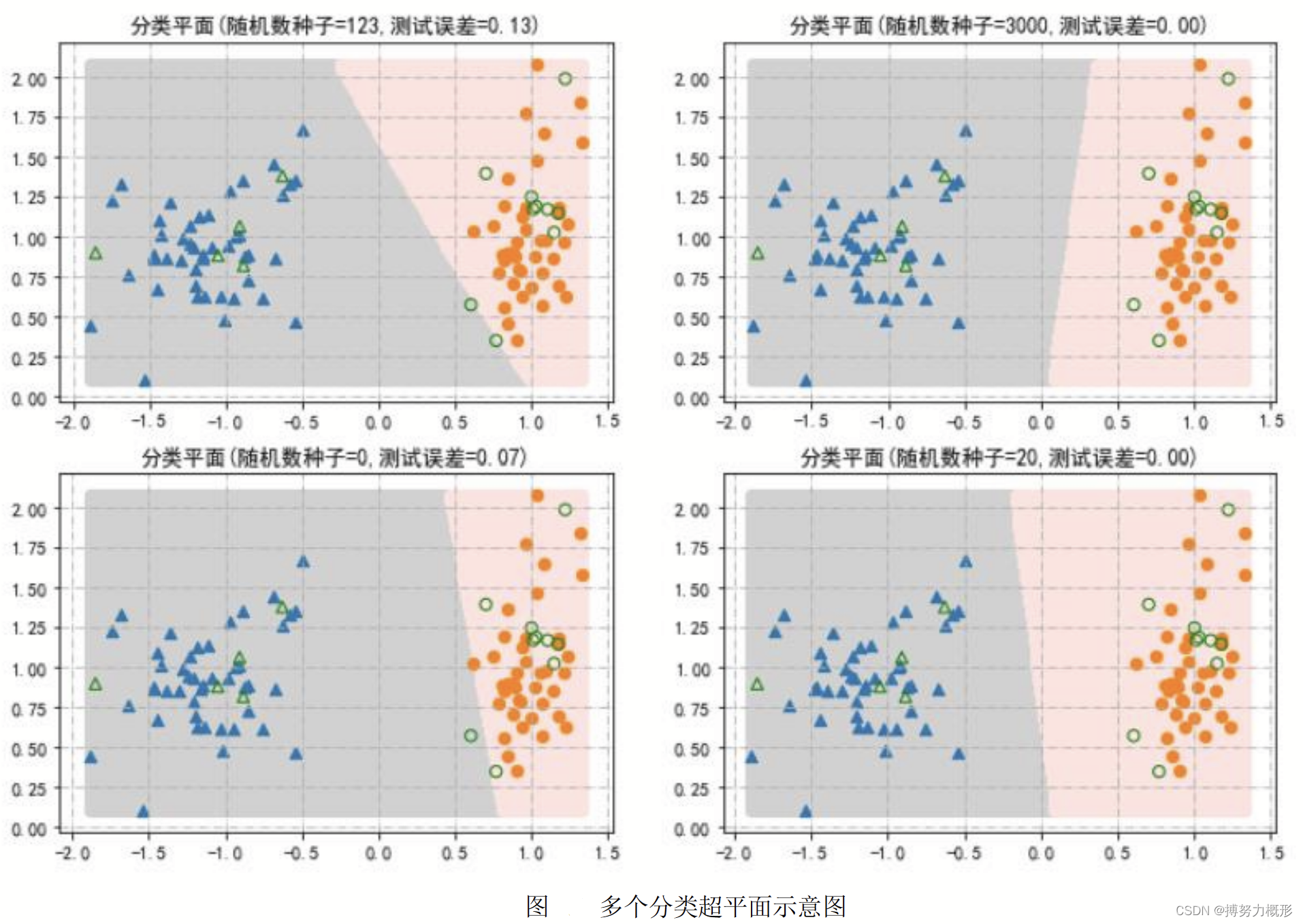
以二维空间为例，如上右侧两图，分类超平面为两种背景颜色的分界线，此时超平面方程为 $b+w_{1}X_{1}+w_{2}X_{2}=0$ ，其中， $X_{1},X_{2}$ 为两个维度。

拓展到p维空间，则超平面方程变为 $b+w_{1}X_{1}+w_{2}X_{2}+\cdots +w_{p}X_{p}=0$ ，即 $b+w^{T}X=0$ ，分类超平面的位置由待估参数b和w确定。

预测时，将某个待预测点代入包含参数估计值的式子 $\widehat{b}+\widehat{w}^{T}X$ 中，该预测点因式子大于或小于0而分别位于超平面两侧，因此输出变量分别为-1或1.

上左两图中的分界线为使用三层神经网络得到的分界面，对比来说，支持向量分类确定的超平面是具有最大边界的超平面，因此，它的优点在于：① 由较高预测置信度，因为超平面距两侧边缘点比一般的预测更远；② 最大边界超平面仅取决于两类的边缘观测点，从而有利于克服过拟合问题，具有很强的鲁棒性（Robustness）。

3. 求解：参数的拉格朗日乘数法求解

完全线性可分下的二维空间为例，步骤为：

1）找出可能的超平面。分别将两类最外侧样本观测点连线，形成两个多边形，称为两类样本集的凸包（Convex Hull），然后，以一类的凸包边界维基准线，找另一类凸包边界上的点，过该点做基准线的平行线，得到一对平行线，该平行线垂线的中垂线为对应的超平面。显然，可以找出很多个这样的超平面，下面找出平行线相距最远的对应的最大边界超平面。

2）若以 $y_{i}=1$ 类凸包边界 $b+w^{T}X^{+}=1$ 为基准线，超平面方程为 $b+w^{T}X=0$ ，则平行线为 $b+w^{T}X^{-}=-1$ ，那么平行线间的距离为 $\lambda =\frac{2}{\left \| w \right \|},\left \| w \right \|=\sqrt{w^{T}w}$ ；

3）若要使 $y_{i}=1/-1$ 预测正确，则有 $b+w^{T}X_{i}\geq/\leq 1$ ，因此有 $y_{i}(b+w^{T}X_{i})\geq 1$ .要使平行线间距离最大，则要 $\left \| w \right \|$ 最小，为求解方便，即为 $\tau \left ( w \right )=\frac{1}{2}\left \| w \right \|^{2}=\frac{1}{2}w^{T}w$ 最小，因此有超平面参数求解的凸二次型规划问题：

$\left\{\begin{matrix} \underset{min}{\tau} (w)=\frac{1}{2}\left \| w \right \|^{2}=\frac{1}{2}w^{T}w\\s.t.\, \: \; \; y_{i}(b+w^{T}X_{i})-1\geq 0,i=1,2,...,N\end{matrix}\right.$

此规划问题使用拉格朗日乘数法求解。假设目标函数为 $f(X)=X_{1}^{2}+X_{2}^{2},g(X)=X_{1}+X_{2}-1\leq 0$ 或 $g(X)=X_{1}+X_{2}+1\leq 0$ ，f(X)的等高线图和g(X)≤0的图像如下图所示，

4. 预测：支持向量分类的预测

对新样本进行预测时，只需将样本X代入式子 $b+w^{T}X$ 并且关注其符号：

$h(X)=Sign(b+w^{T}X)=Sign\left [ b+\sum_{i=1}^{L}\left ( a_{i}y_{i}X_{i}^{T} \right )X \right ]=Sign\left [ b+\sum_{i=1}^{L} a_{i}y_{i}(X_{i}^{T}X) \right ]$

其中Xi为支持向量，共有L个支持向量。若h(X)>0，则y^hat=1；若h(X)<0，则y^hat=-1.

5. 应用：python实例与代码

通过生成的模拟数据，展示完全线性可分下的最大边界超平面。

#导入模块
import numpy as np
from numpy import random
import pandas as pd
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import warnings
warnings.filterwarnings(action = 'ignore')
%matplotlib inline
plt.rcParams['font.sans-serif']=['SimHei']  #解决中文显示乱码问题
plt.rcParams['axes.unicode_minus']=False
from sklearn.datasets import make_classification,make_circles,make_regression
from sklearn.model_selection import train_test_split,KFold
import sklearn.neural_network as net
import sklearn.linear_model as LM
from scipy.stats import multivariate_normal
from sklearn.metrics import r2_score,mean_squared_error,classification_report
from sklearn import svm
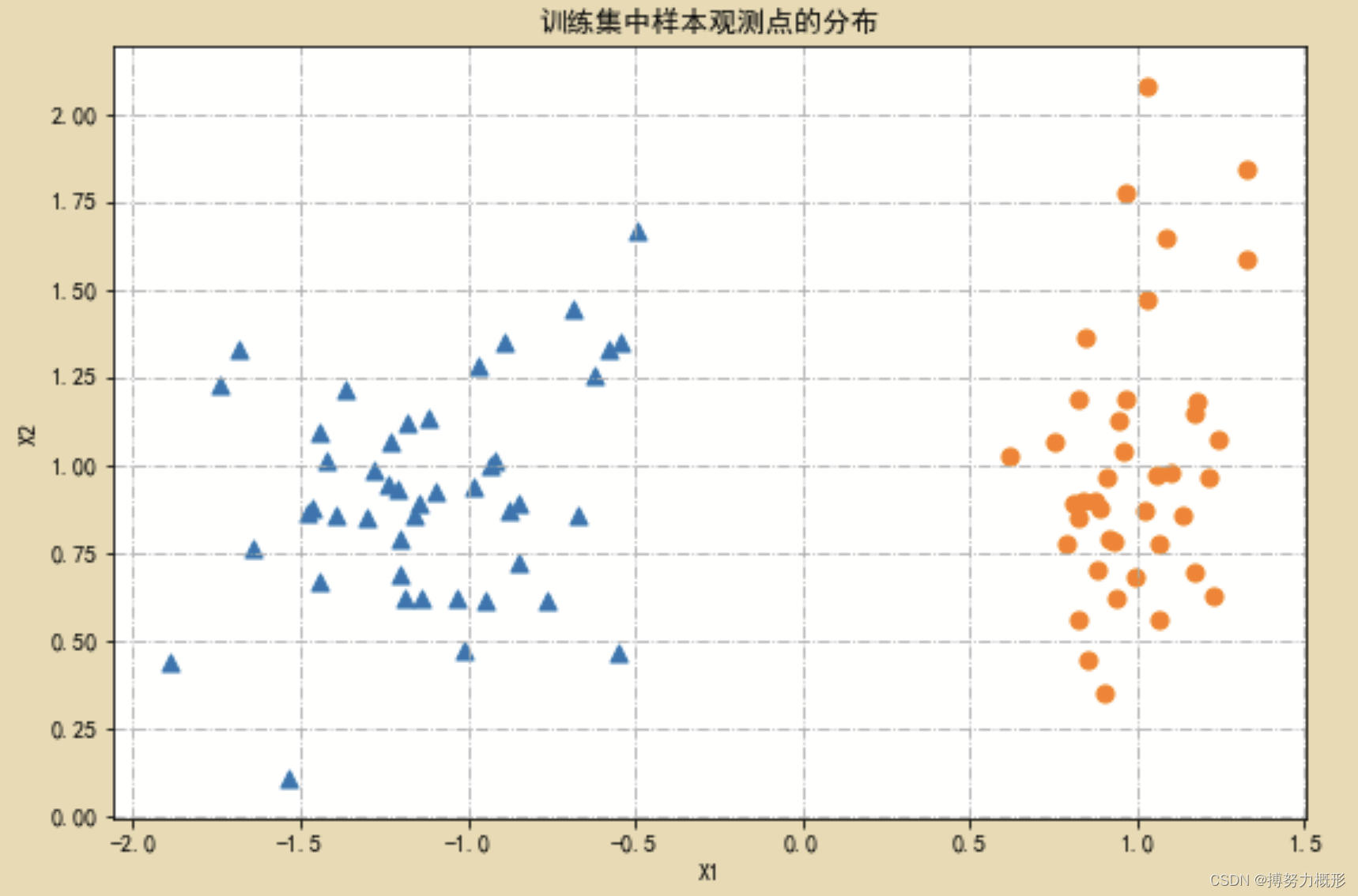
import os

# 生成模拟数据并可视化
N=100
X,Y=make_classification(n_samples=N,n_features=2,n_redundant=0,n_informative=2,class_sep=1,random_state=1,n_clusters_per_class=1)plt.figure(figsize=(9,6))
X_train, X_test, Y_train, Y_test = train_test_split(X,Y,train_size=0.85, random_state=123)
markers=['^','o']
for k,m in zip([1,0],markers):plt.scatter(X_train[Y_train==k,0],X_train[Y_train==k,1],marker=m,s=50)
plt.title("训练集中样本观测点的分布")
plt.xlabel("X1")
plt.ylabel("X2")
plt.grid(True,linestyle='-.')
plt.show()

模拟数据的分布情况为：

接下来使用支持向量机求出最大边界超平面：

N=100
X,Y=make_classification(n_samples=N,n_features=2,n_redundant=0,n_informative=2,class_sep=1,random_state=1,n_clusters_per_class=1)
X_train, X_test, Y_train, Y_test = train_test_split(X,Y,train_size=0.85, random_state=123)
X1,X2= np.meshgrid(np.linspace(X_train[:,0].min(),X_train[:,0].max(),500),np.linspace(X_train[:,1].min(),X_train[:,1].max(),500))
X0=np.hstack((X1.reshape(len(X1)*len(X2),1),X2.reshape(len(X1)*len(X2),1)))
modelSVC=svm.SVC(kernel='linear',random_state=123,C=2) #modelSVC=svm.LinearSVC(C=2,dual=False)
modelSVC.fit(X_train,Y_train)
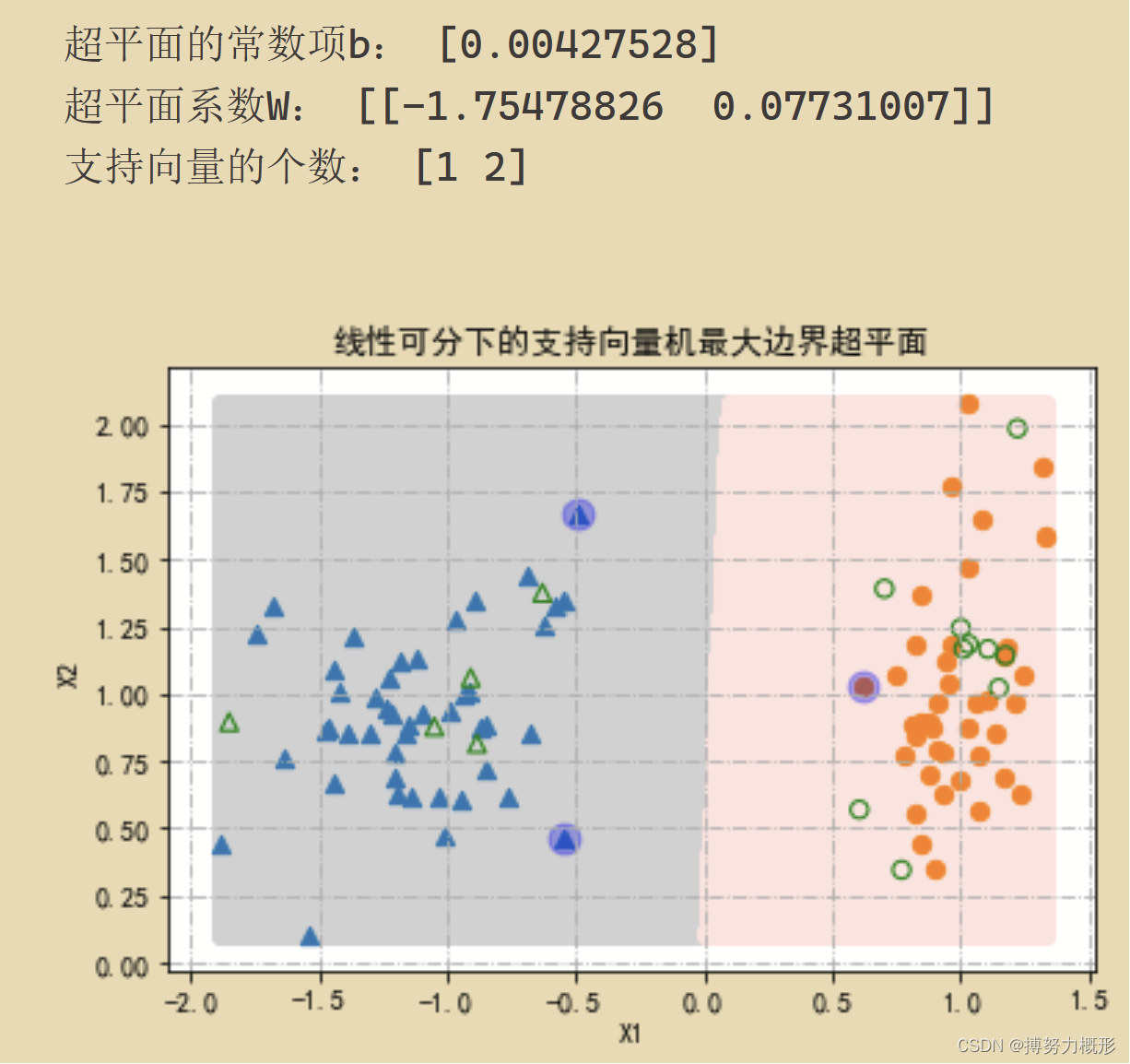
print("超平面的常数项b：",modelSVC.intercept_)
print("超平面系数W：",modelSVC.coef_)
print("支持向量的个数：",modelSVC.n_support_)
Y0=modelSVC.predict(X0)
plt.figure(figsize=(6,4)) 
plt.scatter(X0[np.where(Y0==1),0],X0[np.where(Y0==1),1],c='lightgray')
plt.scatter(X0[np.where(Y0==0),0],X0[np.where(Y0==0),1],c='mistyrose')
for k,m in [(1,'^'),(0,'o')]:plt.scatter(X_train[Y_train==k,0],X_train[Y_train==k,1],marker=m,s=40)plt.scatter(X_test[Y_test==k,0],X_test[Y_test==k,1],marker=m,s=40,c='',edgecolors='g')plt.scatter(modelSVC.support_vectors_[:,0],modelSVC.support_vectors_[:,1],marker='o',c='b',s=120,alpha=0.3)
plt.xlabel("X1")
plt.ylabel("X2")
plt.title("线性可分下的支持向量机最大边界超平面")
plt.grid(True,linestyle='-.')
plt.show()

结果为：