动态规划二：二维动态规划(18308+11077+19187+17089)

本文主要是介绍动态规划二：二维动态规划(18308+11077+19187+17089)，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

（一）前言

线性动态规划只需考虑一个变量，而二维动规需要两个变量来实现动态规划方程。定义两个变量需要根据具体问题具体分析。常见的二维动规问题类型个人划分为以下几种类型：（1）字符串DP（2）N区间M问题（3）矩阵类DP问题（4）区间动态规划（单独介绍）（5）背包问题（单独介绍）。其中4和5虽然也采用二维形式，但问题比较典型，一般被划分为专有类别，因此本文不做具体阐述。

（二）字符串DP

顾名思义，字符串DP就是针对字符串上一些问题的动态规划算法。基础性问题有四大类：最长公共子序列、最长公共子串、最长回文子序列、最长回文子串。

（1）最长公共子序列（18308 最长公共子序列）

给定两个字符串A和B，请输出这两个字符串的最大公共子序列

问题分析：暴力枚举算法必须先求出一个字符串的所有子序列，再和另一个字符串进行验证，复杂度较高。动态规划方法定义dp[i][j] 为A串前i个字符，B串前j个字符的最大公共子序列长度。

此类问题我们要首先思考下递归结束条件是否存在？显然如果i==1，那么j等于任意都能很容易求出来，而j==1，i等于任意同理。在此基础上，思考dp[i][j]的动态规划方程。由于是求公共子序列，基于贪心的思想,当A[i]==B[j]时，我们必然选择这个A[i]作为公共子序列最后一个字符，那么dp[i][j] = dp[i-1][j-1] +1。如果A[i]！=B[j]，那么A[i] 和 B[j]必然有一个（也可能两个都）对公共子序列无用，不可能A[i] 和 B[j]都出现在最终的公共子序列中，此时问题就可以划分为两种情况

dp[i][j] = max(dp[i-1][j] ,dp[i][j-1]) ，取两种情况最大值。

#include <iostream>  using namespace std;
int dp[1005][1005];
int main()
{   int i,j;string s,t;cin>>s>>t;for(i=1; i<=s.size(); i++)for(j=1; j<=t.size(); j++)if(s[i-1]==t[j-1])dp[i][j]=dp[i-1][j-1]+1;elsedp[i][j]=max(dp[i-1][j],f[i][j-1]);cout<<dp[s.size()][t.size()];return 0;}

（2）最长公共子串（11077 最长公共子字符串）

求两个输入序列的最长的公共子字符串的长度。子字符串中的所有字符在源字符串中必须相邻。如A字符串：21232523311324和B字符串312123223445，他们的最长公共子字符串为21232，长度为5。

问题分析：暴力作法可以先求出A串全部子串，再和B串做模式匹配。动规作法时，定义dp[i][j]和上一题目略有区别，插播一个小知识。

动态规划方程定义的两种方式，dp[i]的设定：一种是定义到第i个位置的最优解，第二种定义到第i个位置，且求解中必须选中第i个元素的最优值。有些题目两种定义方法均可，有些必须使用第二种，本题目就必须使用第二种定义方法。

定义dp[i][j] 为A[i]和B[j]为最后一个字符的最长公共子串，且A[i]和B[j]必然为公共子串最后一个元素。如果A[i]！=B[j]，显然无法得到公共子串，那么dp[i][j]=0。当A[i]==B[j]时，我们必然选择这个A[i]作为公共子串最后一个字符，那么dp[i][j] = dp[i-1][j-1] +1。逆向思考下，如果A[i-1]和B[j-1]不相等，那么dp[i][j]只能是1，而如果A[i-1]==B[j-1],那么dp[i-1][j-1]一定非0，可以在此基础上得到更长的公共子串。

#include <iostream>#include <cstdio>#include <cstring>using namespace std;
int dp[1005][1005];
int main()
{   char a[10005],b[10005];int i,j,m,n,ans=0,mi=0,mj=0;scanf("%s",a+1);scanf("%s",b+1);m=strlen(a+1),n=strlen(b+1); for(i=1; i<=m; i++) /**< dp[i][j],a的第i和b的第j个是最后一个相同字符 */for(j=1; j<=n; j++){if(a[i]==b[j])dp[i][j]=dp[i-1][j-1]+1;if(ans<dp[i][j]) /**< 记录最大值，方便后面输出公共子串 */{ans=dp[i][j];mi=i,mj=j;}}cout<<ans<<endl;for(i=mi-ans+1;i<=mi;i++)cout<<a[i];return 0;}

（3）最长回文子序列

最长回文子序列和最长回文子串都可以使用上述介绍的算法。当给我们一个字符串A，要求得到A的最长回文子序列时，可以先构造一个字符串B（B为A的逆序），然后对A和B求最长公共子序列。回文子串同理。

此问题的标准DP方法采用区间式处理方法，定义dp[i][j]为区间 A[i]至A[j]的最长回文子序列。

如果 A[i]==A[j]，贪心思想一定可以选择A[i]和A[j]最为回文子序列第一个和最后一个字符。那么dp[i][j] = dp[i+1][j-1] +2；

如果 A[i]！=A[j]，那么A[i]和A[j]至少有一个对回文子序列不做任何贡献，此时问题可以化简

dp[i][j] = max (dp[i+1][j], dp[i][j-1])；

（4）最长回文子串（18922 最长回文子串）

最长回文子串属于经典问题，有暴力，DP，字符串哈希，马拉车等多种方法，网上题解很多。而DP算法效率相对较低，本文不做深入介绍。

（5）其他样例分析

1276：【例9.20】编辑距离

设A和B是两个字符串。我们要用最少的字符操作次数，将字符串A转换为字符串B。这里所说的字符操作共有三种：1、删除一个字符；2、插入一个字符；3、将一个字符改为另一个字符。对任意的两个字符串A和B，计算出将字符串A变换为字符串B所用的最少字符操作次数。

分析：定义dp[i][j] 为A[i]和B[j]为最后一个字符的最少操作次数，那么如果A[i]==B[j]时，最后一个字符无需变换，那么dp[i][j] = dp[i-1][j-1] 。如果A[i]！=B[j]，那么可以A增加一个字符等于B[j]：即

dp[i][j] = dp[i][j-1]+1,或者A删除一个字符：dp[i][j] = dp[i-1][j]+1，或者A[i]修改为B[j]：dp[i][j] = dp[i-1][j-1]+1。

书后习题3-17

分析：定义dp[i][j] 为A[i]和B[j]为最后一个字符的最少距离，那么如果A[i]==B[j]时，最后一个字符距离为0，那么dp[i][j] = dp[i-1][j-1] （是否注意到这个分析部分几乎每个题都一样，~~其实此题目无需分析相等情况~~）。如果A[i]！=B[j]，第一种是A[i]和B[j]直接计算dp[i][j] = dp[i-1][j-1]+A匹配B的距离。第二种A[i]去和空格匹配，这样A的前i-1个和B的前j个匹配：dp[i][j] = dp[i-1][j]+A匹配空格的距离，第三种B[j]去和空格匹配，这样A的前i个和B的前j-1个匹配：dp[i][j] = dp[i][j-1]+B匹配空格的距离。

（三）N区间M问题

此类问题一般形式：在一个长度为N的线性区间内，选择（或插入）M个数据元素，得到某种最优解。在设计算法时，与线性DP区别是增加了一个M个的限制，因此在处理此类问题时，必须先处理M-1问题，才能得到M问题。

（1）19187 广告牌最佳安放问题（二）

有一条路从西向东T公里，是一段旅行的公路。
在这段公路上放置n块广告牌，广告牌的地点：x1,x2,...,xn。
如果你放一块广告牌在地点xi，就能获得ri的收益(ri>0)。该地公路局规定：两块广告牌不能小于或等于5公里。现在请你挑选m个广告牌的放置地点，使得你的总收益在公路局规定的限制下达到最大。
PS：本题目的数据确保一定能放置K块广告牌。

分析：和17098 广告牌最佳安放问题不同的是，题目增加了一个M块广告牌的限制。需要使用二维dp数组。定义dp[i][j]为前i个位置，放j块广告牌的最大收益。如果第i个位置不放广告牌，那么

dp[i][j]=dp[i-1][j]。如果第i个位置放置广告牌，那么前一个广告牌和i的距离必须大于5才行，因此需要找到左侧第一个满足条件的广告牌k，那么dp[i][j] = dp[k][j-1] +ri。

#include <bits/stdc++.h>using namespace std;
int t,n,m,a[1005],b[1005],dp[1005][1005];
int main()
{   int i,j,k;cin>>t>>n>>m;for(i=1;i<=n;i++)cin>>a[i];for(i=1;i<=n;i++)cin>>b[i];for(j=1;j<=m;j++){for(i=j;i<=n;i++){ /**< dp[i][j]，前i个位置选择j个广告牌的最优值 */dp[i][j]=dp[i-1][j];/**< 第一种情况，第i个位置不放广告牌 */for(k=i-1;k>=j-1;k--)if(a[i]-a[k]>5) /**< k位置和i位置距离大于5，前k个放j-1个牌，i位置放第j个牌*/dp[i][j]=max(dp[i][j],dp[k][j-1]+b[i]);/**< 其实这里一旦有满足条件的a[k]就可以break了 */}}cout<<dp[n][m];return 0;}

（2）17089 最大m子段和

“最大m子段和”问题：给定由n个整数（可能为负）组成的序列a1、a2、a3、...、an，以及一个正整数m，
要求确定序列的m个不相交子段，使这m个子段的总和最大！m是子段的个数。当m个子段的每个子段和都是负值时，定义m子段和为0。

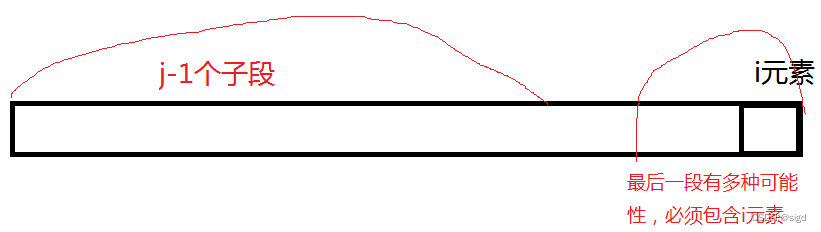
分析：如果说最大子段和还可以看成是一种求极值问题，那么最大M子段和显然是动态规划问题，仍采用前述的分析方法，定义dp[i][j]为前i个元素，j个子段和的最大值。如果最后一个子段不包含第i元素，那么dp[i][j]=dp[i-1][j]。如果最后一个子段包含i元素，那么最后一段可能性比较多，必须枚举所有以i为最后一个元素的子段。

#include <iostream> typedef long long ll;
using namespace std;
ll n,m,a[10005]= {0},sum[10005],dp[1005][1005]= {0};
int main()
{   ios::sync_with_stdio(0),cin.tie(0);int i,j,k;cin>>n>>m;for(i=1; i<=n; i++) /**< sum前缀和数组 */cin>>a[i],sum[i]+=sum[i-1]+a[i];for(j=1; j<=m; j++){for(i=j; i<=n; i++){/**< dp[i][j]前i个元素j子段最大值 */if(i==j) /**< 只能一个元素一段 */dp[i][j]=sum[i];else{dp[i][j]=dp[i-1][j];/**< 最后一个子段不包含i元素，那么dp[i][j]=dp[i-1][j]*/for(k=i; k>=j-1&&k>=1; k--) /**< 枚举所有以i为最后一个元素的子段[k,i] */dp[i][j]=max(dp[i][j],dp[k-1][j-1]+sum[i]-sum[k-1]);}}}cout<<max(0LL,dp[n][m]);/**< 当m个子段的每个子段和都是负值时，定义m子段和为0。 */return 0;}