本文主要是介绍《数据挖掘》第六课笔记,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
《数据挖掘》第六课笔记
- 一、蒙特卡罗思想之接受-拒绝采样
- 二、马尔可夫链
- 1.马尔可夫链定义
- 2.马尔可夫链状态的分类和性质
- 2.1 状态的分类
- 2.2 状态的性质
- 2.3 平稳分布(不变分布)与极限分布
- 3.基于马尔可夫链采样
- 4.一阶马尔科夫链模型(牛市熊市股票例子)
- 三、隐马尔可夫链基本定义
- 1.隐马氏模型的组成和基本假设
- 2.隐马氏模型的3个基本问题
- 3.隐马氏模型的应用
- 四、隐马尔可夫链的概率计算问题求解方法
- 1.暴力求解
- 2.前向算法
- 五、隐马尔可夫链的预测问题求解办法之viterbi维特比算法
- 1.`算法(维特比算法)`
- 2.盒球模型
- 3.东京天气预测问题
- 3.1手写计算
- 3.2 code
- 3.3 answer
一、蒙特卡罗思想之接受-拒绝采样
在计算积分值时,蒙特拉洛的主要内容就是从假设分布中抽取n次,估计积分值。对于概率分布不是常见的分布,一个可行的办法是采用接受-拒绝采样来得到该分布的样本。既然 p ( x ) p(x) p(x)太复杂在程序中没法直接采样,那么我设定一个程序可采样的分布 q ( x ) q(x) q(x) 比如正态分布,然后按照一定的方法拒绝某些样本,以达到接近 p ( x ) p(x) p(x) 分布的目的。
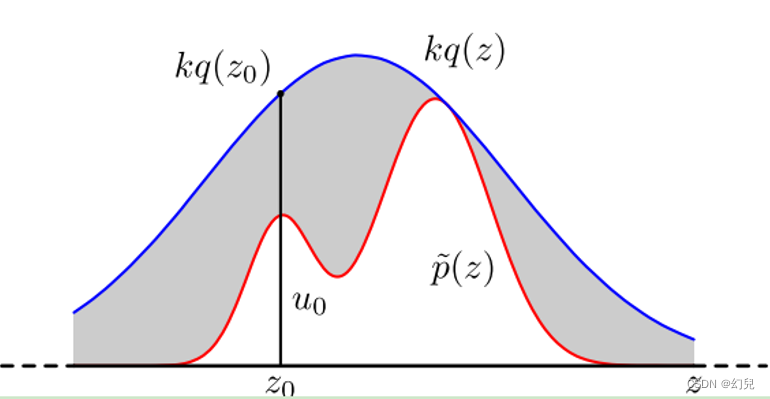
具体采用过程如下,设定一个方便采样的常用概率分布函数 q ( x ) q(x) q(x),以及一个常量 k k k,使得 p ( x ) p(x) p(x)总在 k q ( x ) kq(x) kq(x) 的下方,如上图。
首先,采样得到 q ( x ) q(x) q(x)的一个样本 z 0 {z_0} z0,然后,从均匀分布 ( 0 , k q ( z 0 ) ) (0,kq({z_0})) (0,kq(z0))中采样得到一个值 u u u。如果 u u u落在了上图中的灰色区域,则拒绝这次抽样,否则接受这个样本 z 0 {z_0} z0。重复以上过程得到 n n n个接受的样本 z 0 , z 1 , … z n − 1 {z_0},{z_1}, \ldots {z_{n - 1}} z0,z1,…zn−1,则最后的蒙特卡罗求解结果为: p ( z i ) k q ( z i ) {\frac{{p({z_i})}}{{kq({z_i})}}} kq(zi)p(zi) 整个过程中,我们通过一系列的接受拒绝决策来达到用 q ( x ) q(x) q(x)模拟 p ( x ) p(x) p(x)概率分布的目的。
二、马尔可夫链
1.马尔可夫链定义
随机过程 { X n , n = 0 , 1 , 2 , … L } \{{X_{\rm{n}}},n = 0,1,2, \ldots L\} {Xn,n=0,1,2,…L}称为Markov链,若它只取有限值或可列个值(称为过程的状态,记为0,1,2,…),{0,1,2…}或者其子集记为S,称为过程的状态空间,对任意 n n n ≥ \ge ≥ 0 0 0,及状态 i , j , i 0 , i 1 , L , i n − 1 i,j,{i_0},{i_1},L,{i_{n - 1}} i,j,i0,i1,L,in−1,有(马氏性) P ( X n + 1 = j ∣ X 0 = i 0 , X 1 = i 1 , L , X n − 1 = i n − 1 , X n = i ) = P ( X n + 1 = j ∣ X n = i ) \color{red}P({X_{n + 1}} = j|{X_0} = {i_0},{X_1} = {i_1},L,{X_{n - 1}} = {i_{n - 1}},{X_n} = i) = P({X_{n + 1}} = j|{X_n} = i) P(Xn+1=j∣X0=i0,X1=i1,L,Xn−1=in−1,Xn=i)=P(Xn+1=j∣Xn=i) 即马尔可夫链 { X n , n ≥ 0 } \{ {X_{\rm{n}}},n \ge 0\} {Xn,n≥0}的有限维分布完全由初始分布 P { X 0 = i 0 } P\{ {X_0} = {i_0}\} P{X0=i0}和条件概率(一步转移概率) P ( X n = j ∣ X n − 1 = i ) P({X_{n }} = j|{X_{n-1}} = i) P(Xn=j∣Xn−1=i)确定
2.马尔可夫链状态的分类和性质
2.1 状态的分类
定义1:若存在 n n n ≥ \ge ≥ 0 0 0使得 P i j ( n ) P_{ij}^{(n)} Pij(n) > \gt > 0 0 0,则称从状态 i i i可达状态 j j j,记 i → j i \to j i→j。如果 i → j i \to j i→j且 j → i j \to i j→i,则称 i i i和 j j j互通,记 i ↔ j \color{red}i \leftrightarrow j i↔j
将任何两个互通的状态归为一类:(1)同一类的状态之间都是互通的.(2)任何一个状态不能同时属于两个不同的类。
定义2:若Markov链只存在一个类,就称它是不可约的,否则称为可约的
2.2 状态的性质
定义3:若集合 { n : n ≥ 1 , P i i ( n ) > 0 } ≠ ∅ \{ n:n \ge 1,P_{ii}^{(n)} > 0\} \ne \emptyset {n:n≥1,Pii(n)>0}=∅,则称它的最大公约数 d = d ( j ) d=d(j) d=d(j)为状态 i i i的周期,若 { d = 1 , 称 i 为非周期的 d > 1 , 称 i 为周期的 \color{red}\{ _{d = 1,称i为非周期的}^{d > 1,称i为周期的} {d=1,称i为非周期的d>1,称i为周期的特.若上述集合为空集,则称$i$的周期为无穷大
定理:若状态 i , j i,j i,j同属一类,则 d ( i ) = d ( j ) d(i)=d(j) d(i)=d(j)
2.3 平稳分布(不变分布)与极限分布
平稳分布:设马氏链 { X n , n ≥ 0 } \{ {X_{\rm{n}}},n \ge 0\} {Xn,n≥0}有转移概率矩阵 P = ( P i j ) P{\rm{ = (}}{{\rm{P}}_{{\rm{ij}}}}{\rm{)}} P=(Pij),若存在一个概率分布 { π i , i ∈ S } \{ {\pi _i},i \in S\} {πi,i∈S},满足 π j = ∑ i ∈ S π i P i j {\pi _j} = \sum\limits_{i \in S} {{\pi _i}{P_{ij}}} πj=i∈S∑πiPij,则称 { π i , i ∈ S } \color{red}\{ {\pi _i},i \in S\} {πi,i∈S}为该链的平稳分布(不变分布)
分析:
令 π = ( π 1 , π 2 , … ) \pi = ({\pi _1},{\pi _2}, \ldots ) π=(π1,π2,…),则上式为 π = π P \pi = \pi P π=πP
(1).由 π = π P \pi = \pi P π=πP可知, π ( I − P ) = 0 \pi (I - P) = 0 π(I−P)=0,故 I I I是矩阵 P P P的左特征值,平稳分布 π \pi π是 P P P的左特征向量
(2).两边同乘 P P P,得 π = π P = π P 2 = … = π P n \pi = \pi P = \pi {P^2} = \ldots = \pi {P^n} π=πP=πP2=…=πPn
极限分布:称Markov链是遍历的,如果所有状态相通且均是周期为1的正常返状态,对于遍历的Markov链,极限 lim n → ∞ P i j ( n ) = π j = 1 u j \color{red}\mathop {\lim }\limits_{n \to \infty } P_{ij}^{(n)} = {\pi _j} = \frac{1}{{{u_j}}} n→∞limPij(n)=πj=uj1, j ∈ S j \in S j∈S称为Markov链的极限分布
3.基于马尔可夫链采样
如果我们得到了某个平稳分布所对应的马尔科夫链状态转移矩阵 P P P,我们就很容易采用出这个平稳分布的样本集。
假设我们任意初始的概率分布是 π 0 ( x ) \pi_0(x) π0(x),经过第一轮马尔科夫链状态转移后的概率分布是 π 1 ( x ) \pi_1(x) π1(x),第 i i i轮的概率分布 π i ( x ) \pi_i(x) πi(x)。 假设经过 n n n轮后马尔科夫链收敛到我们的平稳分布 π ( x ) \pi(x) π(x),即: π n ( x ) = π n + 1 ( x ) = π n + 2 ( x ) = … = π ( x ) {\pi _n}(x) = {\pi _{n + 1}}(x) = {\pi _{n + 2}}(x) = \ldots = \pi (x) πn(x)=πn+1(x)=πn+2(x)=…=π(x) 对于每个分布 π i ( x ) \pi_i(x) πi(x),我们有: π i ( x ) = π i − 1 ( x ) P = π i − 2 ( x ) P 2 = … = π 0 ( x ) P i {\pi _i}(x) = {\pi _{i - 1}}(x)P = {\pi _{i - 2}}(x){P^2} = \ldots = {\pi _0}(x){P^i} πi(x)=πi−1(x)P=πi−2(x)P2=…=π0(x)Pi 现在我们可以开始采样了,首先,基于初始任意简单概率分布比如高斯分布 π 0 ( x ) \pi_0(x) π0(x)采样得到状态值 x 0 x_0 x0,基于条件概率分布 P ( x ∣ x 0 ) P(x|x_0) P(x∣x0)采样状态值 x 1 x_1 x1 ,一直进行下去,当状态转移进行到一定的次数时,比如到 n n n次时,我们认为此时的采样集 ( x n , x n + 1 , x n + 2 , . . . ) (x_n,x_{n+1},x_{n+2},...) (xn,xn+1,xn+2,...)即是符合我们的平稳分布的对应样本集,可以用来做蒙特卡罗模拟求和了。
总结下基于马尔科夫链的采样过程:
(1)输入马尔科夫链状态转移矩阵 P P P,设定状态转移次数阈值 n 1 n_1 n1 ,需要的样本个数 n 2 n_2 n2
(2)从任意简单概率分布采样得到初始状态值 x 0 x_0 x0
(3) f o r t = 0 t o n 1 + n 2 − 1 for\ t=0\ to\ n_1+n_2−1 for t=0 to n1+n2−1: 从条件概率分布 P ( x ∣ x t ) P(x|x_t) P(x∣xt)中采样得到样本 x t + 1 x_{t+1} xt+1
(4)样本集 ( x n 1 , x n 1 + 1 , . . . , x n 1 + n 2 − 1 ) \color{red}(x_{n_1}, x_{n_1+1},..., x_{n_1+n_2-1}) (xn1,xn1+1,...,xn1+n2−1)即为我们需要的平稳分布对应的样本集。
4.一阶马尔科夫链模型(牛市熊市股票例子)
链接: 《数据挖掘》第二次实验
三、隐马尔可夫链基本定义
1.隐马氏模型的组成和基本假设
组成:
• 初始概率分布
• 状态转移概率分布
• 观测概率分布
• Q:所有可能状态的集合
• V:所有可能观测的集合
• I: 长度为T的状态序列
• O:对应的观测序列
• A:状态转移概率矩阵
• B:观测概率矩阵
• π \pi π:初始状态概率向量
基本假设:
(1)齐次马尔科夫性假设,隐马尔可分链t的状态只和t-1状态有关。
(2)观测独立性假设,观测只和当前时刻状态有关。
2.隐马氏模型的3个基本问题
(1)概率计算问题
给定: λ = ( A , B , π ) \lambda = (A,B,\pi ) λ=(A,B,π) O = ( o 1 , o 2 , ⋯ , o T ) O = ({o_1},{o_2}, \cdots ,{o_T}) O=(o1,o2,⋯,oT)
计算: P ( O ∣ λ ) P(O|\lambda ) P(O∣λ)
(2)学习问题
已知: O = ( o 1 , o 2 , ⋯ , o T ) O = ({o_1},{o_2}, \cdots ,{o_T}) O=(o1,o2,⋯,oT)
估计: λ = ( A , B , π ) \lambda = (A,B,\pi ) λ=(A,B,π),使 P ( O ∣ λ ) P(O|\lambda ) P(O∣λ)最大
(3)预测问题(解码)
已知: λ = ( A , B , π ) \lambda = (A,B,\pi ) λ=(A,B,π) O = ( o 1 , o 2 , ⋯ , o T ) O = ({o_1},{o_2}, \cdots ,{o_T}) O=(o1,o2,⋯,oT)
求:使 P ( O ∣ λ ) P(O|\lambda ) P(O∣λ)最大的状态序列 I = ( i 1 , i 2 , ⋯ , i T ) I = ({i_1},{i_2}, \cdots ,{i_T}) I=(i1,i2,⋯,iT)
3.隐马氏模型的应用
• 人脸识别
• 语音识别
• 入侵检测
• 情报领域
• 手写体识别
• 通信领域的解码器
四、隐马尔可夫链的概率计算问题求解方法
1.暴力求解
1.一个简单问题
知道骰子有几种,每种骰子是什么,每次掷的都是什么骰子,根据掷骰子掷出的结果,求产生这个结果的概率。
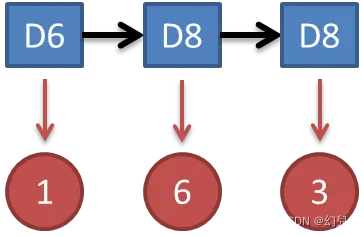
P = P ( D 6 ) ∗ P ( D 6 → 1 ) ∗ P ( D 6 → D 8 ) ∗ P ( D 8 → 6 ) ∗ P ( D 8 → D 8 ) ∗ P ( D 8 → 3 ) P = P(D6)*P(D6 \to 1)*P(D6 \to D8)*P(D8 \to 6)*P(D8 \to D8)*P(D8 \to 3) P=P(D6)∗P(D6→1)∗P(D6→D8)∗P(D8→6)∗P(D8→D8)∗P(D8→3)
= 1 3 ∗ 1 6 ∗ 1 3 ∗ 1 8 ∗ 1 3 ∗ 1 8 = \frac{1}{3}*\frac{1}{6}*\frac{1}{3}*\frac{1}{8}*\frac{1}{3}*\frac{1}{8} =31∗61∗31∗81∗31∗81
2.谁动了我的骰子?
比如说你怀疑自己的六面骰被赌场动过手脚了,有可能被换成另一种六面骰,这种六面骰掷出来是1的概率更大,是1/2,掷出来是2,3,4,5,6的概率是1/10。你怎么办么?
答案很简单,算一算正常的三个骰子掷出一段序列的概率,再算一算不正常的六面骰和另外两个正常骰子掷出这段序列的概率。如果前者比后者小,你就要小心了。比如说掷骰子的结果是:

简单而暴力的方法就是把穷举所有的骰子序列,还是计算每个骰子序列对应的概率相加,得到的总概率就是我们要求的结果。
首先,如果我们只掷一次骰子:

看到结果为1。产生这个结果的总概率可以按照如下计算,总概率为0.18:

把这个情况拓展,我们掷两次骰子
看到结果为1,6。产生这个结果的总概率可以按照如下计算,总概率为0.05:

继续拓展,我们掷三次骰子:
看到结果为1,6,3。产生这个结果的总概率可以按照如下计算,总概率为0.03: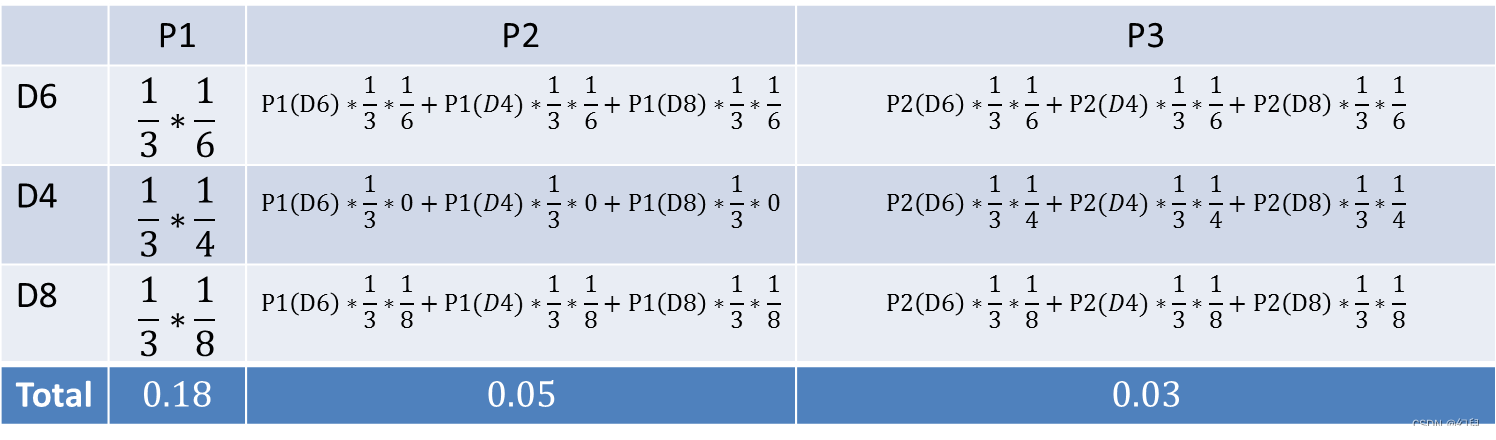
暴力求解算法的时间复杂度是 O ( T N T ) O(T{N^T}) O(TNT)
2.前向算法
仅做一个基本介绍,前向算法的时间复杂度是 O ( N 2 T ) O({N^2}T) O(N2T)
前向概率定义:给定隐马尔可夫模型
定义到时刻 t t t部分观测序列: o 1 , o 2 , ⋯ , o i {o_1},{o_2}, \cdots ,{o_i} o1,o2,⋯,oi,且状态为 q i {q_i} qi的概率为前向概率,记作 α t ( i ) = P ( o 1 , o 2 , ⋯ , o t , i t = q i ∣ λ ) {\alpha _t}(i) = P({o_1},{o_2}, \cdots ,{o_t},{i_t} = {q_i}|\lambda ) αt(i)=P(o1,o2,⋯,ot,it=qi∣λ)
算法(观测序列概率的前向算法)
输入:隐马尔可夫模型 λ \lambda λ,观测序列 O O O
输出:观测序列概率 P ( O ∣ λ ) P(O|\lambda ) P(O∣λ)
初值: α t ( i ) = π i b i ( o 1 ) {\alpha _t}(i) = {\pi _i}{b_{\rm{i}}}({o_1}) αt(i)=πibi(o1), i = 1 , 2 , . . . , N i=1,2,...,N i=1,2,...,N
递推: α t + 1 ( i ) = [ ∑ i = 1 N α t ( j ) α j i ] b i ( o t + 1 ) {\alpha _{t + 1}}(i) = \left[ {\sum\limits_{i = 1}^N {{\alpha _t}(j){\alpha _{ji}}} } \right]{b_i}({o_{t + 1}}) αt+1(i)=[i=1∑Nαt(j)αji]bi(ot+1), i = 1 , 2 , . . . , N i=1,2,...,N i=1,2,...,N
终止: P ( O ∣ λ ) = ∑ i = 1 N α T ( i ) P(O|\lambda ) = \sum\limits_{i = 1}^N {{\alpha _T}(i)} P(O∣λ)=i=1∑NαT(i)
五、隐马尔可夫链的预测问题求解办法之viterbi维特比算法
1.算法(维特比算法)
输入:模型 λ = ( A , B , π ) \lambda = (A,B,\pi ) λ=(A,B,π)和观测 O = ( o 1 , o 2 , ⋯ , o T ) O = ({o_1},{o_2}, \cdots ,{o_T}) O=(o1,o2,⋯,oT)
输出:最优路径 I ∗ = ( i 1 ∗ , i 2 ∗ , ⋯ , i T ∗ ) {I^*} = (i_1^*,i_2^*, \cdots ,i_T^*) I∗=(i1∗,i2∗,⋯,iT∗)
(1)初始化 δ 1 ( i ) = π i b i ( o 1 ) , i = 1 , 2 , . . . N {\delta _1}(i) = {\pi _i}{b_i}({o_1}),i=1,2,...N δ1(i)=πibi(o1),i=1,2,...N ϕ 1 ( i ) = 0 , i = 1 , 2 , . . . N {\phi _1}(i) = 0,i=1,2,...N ϕ1(i)=0,i=1,2,...N (2)递推.对 t = 2 , 3 , . . . , T t=2,3,...,T t=2,3,...,T δ t ( i ) = max 1 ≤ j ≤ N [ δ t − 1 ( j ) a j i ] b i ( o t ) , i = 1 , 2 , . . . N {\delta _t}(i) = \mathop {\max }\limits_{1 \le j \le N} [{\delta _{t - 1}}(j){a_{ji}}]{b_i}({o_t}),i=1,2,...N δt(i)=1≤j≤Nmax[δt−1(j)aji]bi(ot),i=1,2,...N ϕ t ( i ) = arg max 1 ≤ j ≤ N [ δ t − 1 ( j ) a j i ] , i = 1 , 2 , . . . N {\phi _t}(i) = \arg \mathop {\max }\limits_{1 \le j \le N} [{\delta _{t - 1}}(j){a_{ji}}],i=1,2,...N ϕt(i)=arg1≤j≤Nmax[δt−1(j)aji],i=1,2,...N
2.盒球模型

3.东京天气预测问题
一个东京的朋友每天根据天气{下雨,天晴}决定当天的活动{公园散步,购物,清理房间}中的一种,我每天只能在twitter上看到她发的动态“啊,我前天公园散步、昨天购物、今天清理房间了!”,那么我可以根据她发的推特推断东京这三天的天气。
在这个例子里,显状态是活动,隐状态是天气。
3.1手写计算
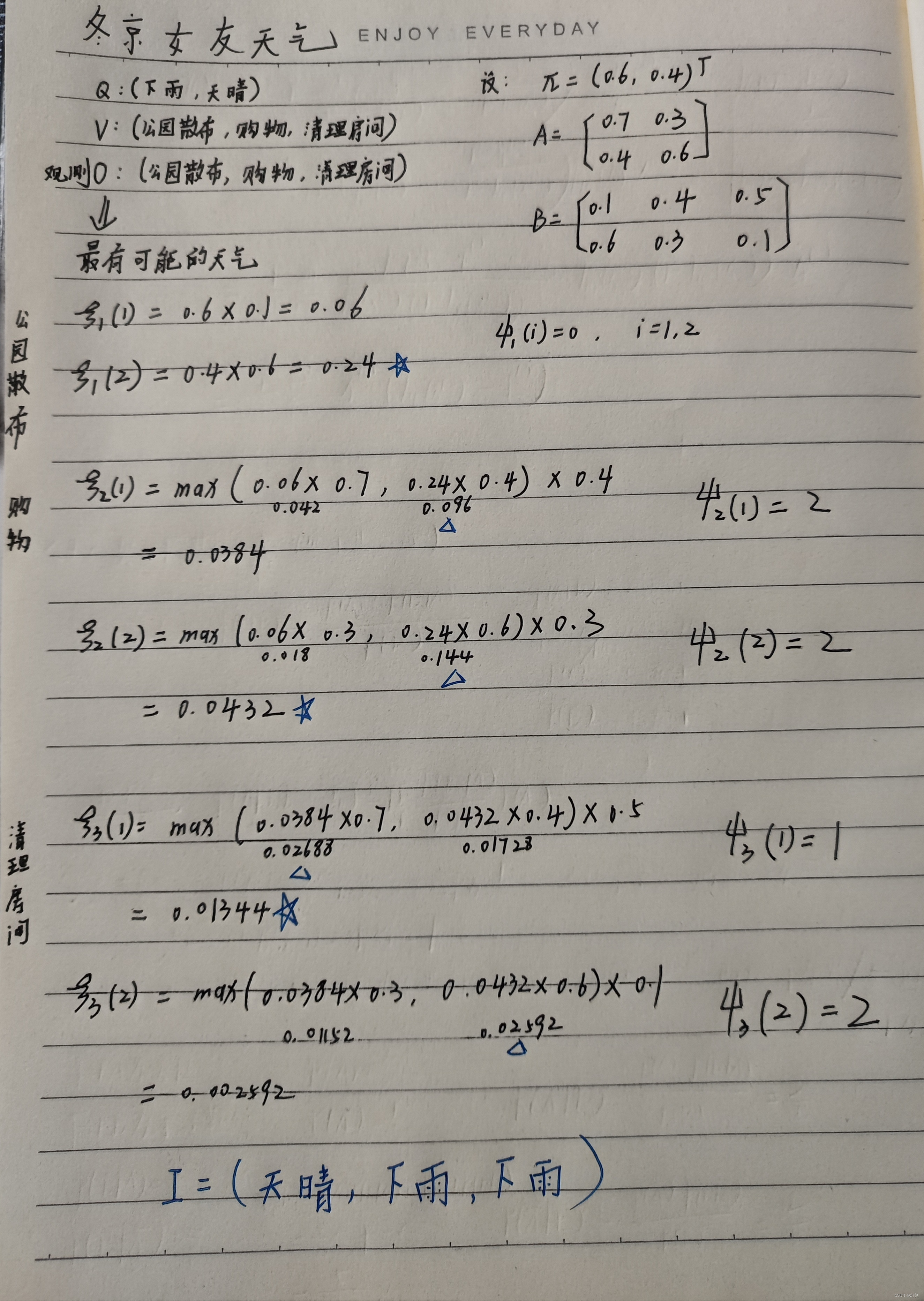
3.2 code
import numpy as npclass HMM():def __init__(self):# 定义天气状态和对应的索引self.states = {'下雨': 0, '天晴': 1}# 定义观测状态和对应的索引self.observations = {'公园散步': 0, '购物': 1, '清理房间': 2}# 定义初始状态概率self.pai = np.array([0.6, 0.4])# 定义状态转移概率self.A = np.array([[0.7, 0.3], [0.4, 0.6]])# 定义观测概率self.B = np.array([[0.1, 0.4, 0.5], [0.6, 0.3, 0.1]])# 观测序列self.O = ['公园散步', '购物', '清理房间']# 维特比算法def viterbi(self):# 初始化T = len(self.O)N = len(self.states)delta = np.zeros((T, N))fai = np.zeros((T, N), dtype=int)# 计算初始状态的deltadelta[0] = self.pai * self.B[:, self.observations[self.O[0]]]# 递推计算delta和faifor t in range(1, T):for j in range(N):temp_delta = delta[t - 1] * self.A[:, j]max_delta_index = np.argmax(temp_delta)delta[t][j] = temp_delta[max_delta_index] * self.B[j][self.observations[self.O[t]]]fai[t][j] = max_delta_index# 回溯找到最优路径path = np.zeros(T, dtype=int)path[T - 1] = np.argmax(delta[T - 1])for t in range(T - 2, -1, -1):path[t] = fai[t + 1][path[t + 1]]
p# 返回最优路径和对应的天气状态weather_sequence = []for p in path:key = list(self.states.keys())[p]weather_sequence.append(key)return weather_sequence,deltaif __name__ == '__main__':HMM=HMM()# 调用维特比算法weather_sequence,delta = HMM.viterbi()# 输出结果print("前天天气:", weather_sequence[0])print("昨天天气:", weather_sequence[1])print("今天天气:", weather_sequence[2])print("概率矩阵为:\n",delta)
3.3 answer

用这个去guess你的女朋友吧~~~~~~~
这篇关于《数据挖掘》第六课笔记的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







