游戏服务端开发：如何精确计算MMO游戏技能攻击区域？

本文主要是介绍游戏服务端开发：如何精确计算MMO游戏技能攻击区域？，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

转自：https://www.gameres.com/493846.html

 

游戏技能攻击区域的计算，关乎服务端的效率。需要确保正确，简洁地计算攻击区域，才能快速寻找攻击对象。

今天只讨论地图上距离的问题。

一般情况下攻击区域分为以下几种：

1.点对点，对个人进行攻击
2.射线攻击，其实就是矩形区域
3.扇形攻击
4.圆形攻击

当然，还有其他情况，例如多区域和其他奇奇怪怪的形状。不过考虑的实际观赏价值，和精度的问题，多区域，只考虑圆形和扇形，其他形状也不考虑了。

释放技能需要几个事物，攻击者，主要被攻击者（也可能是攻击地点），其他围观的群众
 

1. class CPoint//点的定义  
2. {  
3.     double x;  
4.     double y;  
5. }  
6. typedef std::vector<CPoint> SeqCPoint;  
7. double skillDistance = 123;//技能释放距离  
8. CPoint attackerPoint;//攻击者位置  
9. CPoint defenserPoint;//被攻击者位置或技能释放点  
10. SeqCPoint otherRoles;//其他需要检测的角色

下面再细细讲解：

1.点对点的攻击

这个是最简单的，只要达到技能释放的距离，就可以释放。只要攻击者和被攻击者的位置小于配置的skillDistance即可。
 

1. bool isFarThanDistance(CPoint a, CPoint b, double distance)  
2. {  
3.     double x = a.x - b.x;  
4.     double y = a.y - b.y;  
5.     if(x*x + y * y > distance *distance) return true;//超过距离  
6.     return false;//未超过  
7. }  
8.   
9. if (!isFarThanDistance( attackerPoint, defenserPoint, skillDistance) )  
10. {  
11. //在技能范围内，攻击处理  
12. }  

2.射线攻击，矩形区域

怪物向目标喷出一条长长的火线，在火线上的玩家受到攻击，如下图。A向B喷火。同时也要检测周围的玩家是否中招
 

判断一个点是否在矩形内是很简单的，如下：
 

1. //判断点是否在矩阵内  
2. bool inRect( double minx, double miny, double maxx, double maxy, CPoint p)  
3. {  
4.     if(p.x >= minx && p.x <= maxx && p.y >= miny && p.y <= maxy) return true;  
5.     return false;  
6. }  

但这个是在矩形的边跟坐标轴平行的情况下的。如果攻击者的攻击方向跟坐标轴不平行，如上图，就无法计算了

怎么办呢，如果能转换成相对坐标就简单很多了。相对坐标的知识

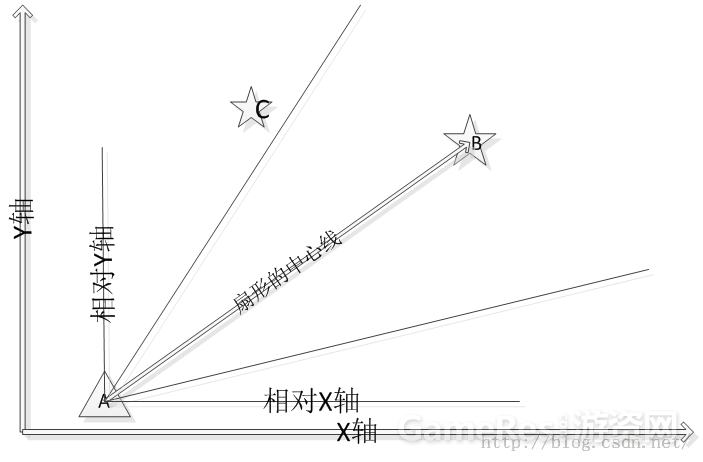
要从绝对坐标转换成相对坐标，需要确定相对坐标的原点和x轴方向。

原点是A点，也就是attackerPoint，X轴方向从A点指向B点。现在是求图中C点的相对坐标。

ABC三点确定位置。根据余弦定理可以求出角CAB的余弦，从而可以求出相对坐标。然后在判断是否在矩阵内。
 

3.扇形区域

攻击者对前方角度α，长度为L的区域进行攻击。如下图，攻击目标为B，要计算旁边的C是否也受到攻击
 

1. //计算两点之间的距离  
2. double computeDistance(CPoint& from, CPoint& to)  
3. {  
4.     return sqrt(pow(to.x - from.x, 2) + pow(to.y - from.y, 2));  
5. }  
6. /** 
7. * 直角坐标--绝对坐标转相对坐标 
8. * originPoint 相对坐标系的原点 
9. * directionPoint 指向x轴方向的点 
10. * changePoint 需要转换的坐标 
11. */   
12. CPoint changeAbsolute2Relative(CPoint originPoint, CPoint directionPoint, CPoint changePoint)  
13. {  
14.        //originPoint为图中A点，directionPoint为图中B点，changePoint为图中C点  
15.     CPoint rePoint;  
16.     if (originPoint == directionPoint)//方向点跟原点重合，就用平行于原坐标的x轴来算就行了  
17.     {//AB点重合，方向指向哪里都没所谓，肯定按原来的做方便  
18.         rePoint.x = changePoint.x - originPoint.x;  
19.         rePoint.y = changePoint.y - originPoint.y;  
20.     }  
21.     else  
22.     {   
23.         //计算三条边  
24.         //计算三条边  
25.         double a = computeDistance(directionPoint, changePoint);  
26.         double b = computeDistance(changePoint, originPoint);  
27.         double c = computeDistance(directionPoint, originPoint);  
28.           
29.         double cosA = (b*b + c*c - a*a) / 2*b*c;//余弦  
30.         rePoint.x = a * cosA ;//相对坐标x  
31.         rePoint.y = sqrt(a*a - rePoint.x*rePoint.x);//相对坐标y  
32.     }  
33.     return rePoint;  
34. }     
35. for(SeqCPoint::iterator iter = otherRoles.begin();  
36.     iter != otherRoles.end();  
37.     iter ++)  
38. {  
39.     //检测每一个角色是否在矩形内。      
40.     CPoint rePoint = changeAbsolute2Relative(attackerPoint, defenserPoint, *iter);//相对坐标  
41.     //skillWidth为图中宽度，skillLong为图中长度  
42.     //宽度是被AB平分的，从A点开始延伸长度  
43.     bool beAttack = inRect(0, - skillWidth/2, skillLong, skillWidth/2, rePoint);//相对坐标下攻击范围不用算了，跟目标的相对坐标算一下  
44.     if (beAttack)  
45.     {  
46.         //受到攻击，攻击处理  
47.     }  
48. }         

扇形，当然是用极坐标最方便，判断一下距离，在半径范围内，然后判断一下角度是否适合。

策划配置：扇形半径R和扇形总角度β

所以构建以A为原点的极坐标。根据中心线的角度α，求出扇形的角度范围为[α-β/2,α+β]。再求出C点的极坐标进行比较
 

今天发现还有一种方法，就是利用向量的点积，可以百度一下。
 

1. void changeXYToPolarCoordinate(Common::CPoint p, double& r, double& angle)  
2. {     
3.     r = sqrt(p.x*p.x + p.y*p.y);//半径  
4.     angle = atan2(p.y , p.x) * 180/PI;//计算出来的是弧度，转成角度，atan2的范围是-π到π之间  
5.     angle = (angle + 360)%360;  
6. }  
7. CPoint changeAbsolute2Relative(CPoint originPoint, CPoint changePoint)  
8. {  
9.     CPoint rePoint;  
10.     rePoint.x = changePoint.x - originPoint.x;  
11.     rePoint.y = changePoint.y - originPoint.y;  
12.     return rePoint;  
13. }  
14. double baseR, baseAngle;  
15. CPoint rePoint = changeAbsolute2Relative(attackerPoint, defenserPoint);//图中B点的相对坐标  
16. changeXYToPolarCoordinate(rePoint, baseR, baseAngle);//转变成极坐标，baseAngle是角度  
17. for(SeqCPoint::iterator iter = otherRoles.begin();  
18.     iter != otherRoles.end();  
19.     iter ++)  
20. {  
21.     CPoint rePointC = changeAbsolute2Relative(attackerPoint, iter2);//图中C点相对坐标   
22.     double cr = 0;//极坐标半径  
23.     double cangle = 0;//极坐标角度  
24.     changeXYToPolarCoordinate(rePointC, cr, cangle);  
25.     if (cr > R)//超过技能半径就无法攻击到了  
26.     {  
27.         continue;  
28.     }  
29.     if ( abs(cangle - baseAngle) < β/2 )//相差的角度小于配置的角度，所以受到攻击。要注意，这里的角度都是在0°到360°之间  
30.     {  
31.         //受到攻击  
32.     }   
33. }  

对于扇形计算面积的优化，可以参考这里

再说一下多个扇形的情况
 

1. CPoint rePoint = changeAbsolute2Relative(attackerPoint, defenserPoint);//图中B点的相对坐标  
2. double longB = sqrt(rePoint.x * rePoint.x + rePoint.y * rePoint.y);//长度  
3. rePoint.x /= longB;  
4. rePoint.y /= longB;//求单位向量  
5. for(SeqCPoint::iterator iter = otherRoles.begin();  
6.     iter != otherRoles.end();  
7.     iter ++)  
8. {  
9.     CPoint rePointC = changeAbsolute2Relative(attackerPoint, iter2);//图中C点相对坐标   
10.     double longC = sqrt(rePointC.x * rePointC.x + rePointC.y * rePointC.y);//长度  
11.     rePointC.x /= longC;  
12.     rePointC.y /= longC;//求单位向量  
13.     double jiaodu = acos(rePoint.x * rePointC.x + rePoint.y * rePointC.y) * 180 /PI;//角CAB的大小  
14.     if（jiaodu < β/2）  
15.     //相差的角度小于配置的角度，所以受到攻击。要注意，这里的角度都是在0°到360°之间  
16.     {  
17.         //受到攻击  
18.     }   
19. }  

分开算就行了，用个for循环，每个扇形分别计算。

4.圆形区域，圆形其实是最简单的了。
 

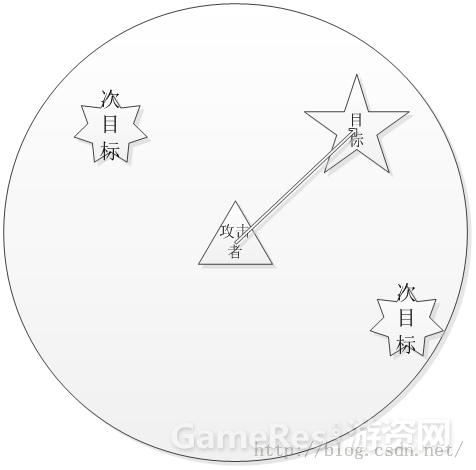
判断是否在攻击者半径范围内就行了。
 

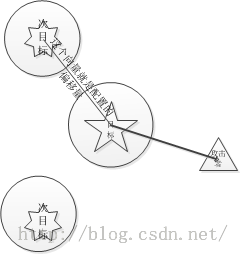
对于多个圆形区域的计算
 

1. for(SeqCPoint::iterator iter = otherRoles.begin();  
2.     iter != otherRoles.end();  
3.     iter ++)  
4. {  
5.     CPoint rePointC = changeAbsolute2Relative(attackerPoint, iter2);//图中C点相对坐标   
6.     double cr = sqrt(rePointC.x*rePoint.x + rePointC.y*rePointC.y); //点到圆心的距离  
7.     if (cr <= R)//超过技能半径就无法攻击到了  
8.     {  
9.         //受到攻击  
10.     }   
11. }     

本质上还是一样，用一个for循环，计算出圆心的位置，然后计算点到圆心的距离就完成了。

这篇关于游戏服务端开发：如何精确计算MMO游戏技能攻击区域？的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---