跳台阶游戏(Python排列组合函数itertools.combinations的应用)

2023-11-22 01:45
文章标签 python 函数 应用 游戏 台阶 排列组合 itertools combinations

本文主要是介绍跳台阶游戏(Python排列组合函数itertools.combinations的应用)，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

给定台阶总数和两种单次可跳级数，编写自定义函数，计算所有的游戏组合方案数量。

(笔记模板由python脚本于2023年11月19日 19:18:48创建，本篇笔记适合熟悉python自定义函数编写，了解排列组合知识的coder翻阅)

【学习的细节是欢悦的历程】

  • Python 官网：https://www.python.org/

  • Free：大咖免费“圣经”教程《 python 完全自学教程》，不仅仅是基础那么简单……
    地址：https://lqpybook.readthedocs.io/

  自学并不是什么神秘的东西，一个人一辈子自学的时间总是比在学校学习的时间长，没有老师的时候总是比有老师的时候多。
            —— 华罗庚

  • My CSDN主页、My HOT博、My Python 学习个人备忘录
  • 好文力荐、 老齐教室
等风来，不如追风去……
给定台阶总数和两种单次可跳级数
跳 台 阶 游 戏
(编写自定义函数，计算所有的游戏组合方案数量)

本文质量分：

【 96 】

本文地址： https://blog.csdn.net/m0_57158496/article/details/134495251

CSDN质量分查询入口：http://www.csdn.net/qc

目 录

  • ◆ 跳台阶游戏
    • 1、题目描述
    • 2、算法解析
      • 2.1 for嵌套
      • 2.2 遍历优化
      • 2.3 求a、b中较少者在a、b总数量中的组合数
    • 3、完整源码


◆ 跳台阶游戏


1、题目描述


  • 题目描述截屏图片
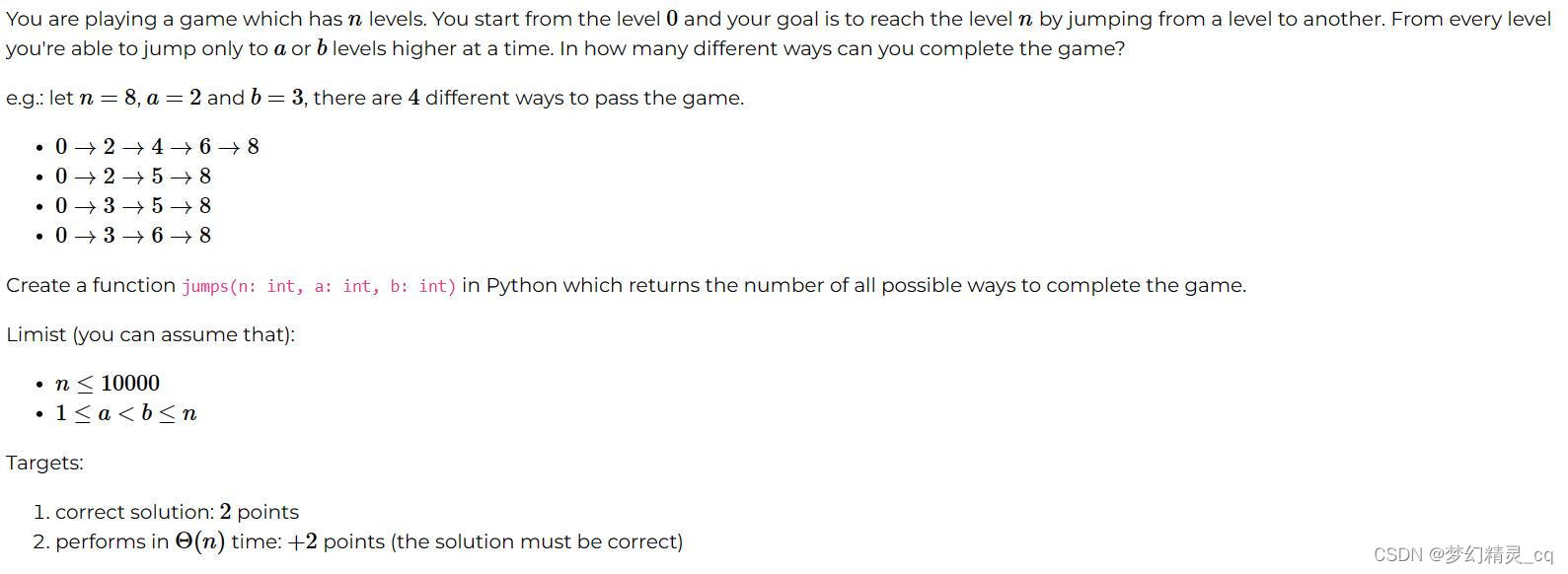
    在这里插入图片描述
     
    题目描述大图
    在这里插入图片描述

【题目来源于 CSDN 问答社区提问“Jump Level Game”】


回页目录

2、算法解析


  我的解法很笨，就是穷举所有a、b组合到levels = n的方案，最后输出总方案数量。(这初期的想法，不切实际啊😂😂)


  • 琢磨到今天中午(2023-11-19 13:27，终于完成代码调试)，终于“完美”解开了跳台阶游戏“谜题”🤗🤗
     
    代码运行效果截屏图片
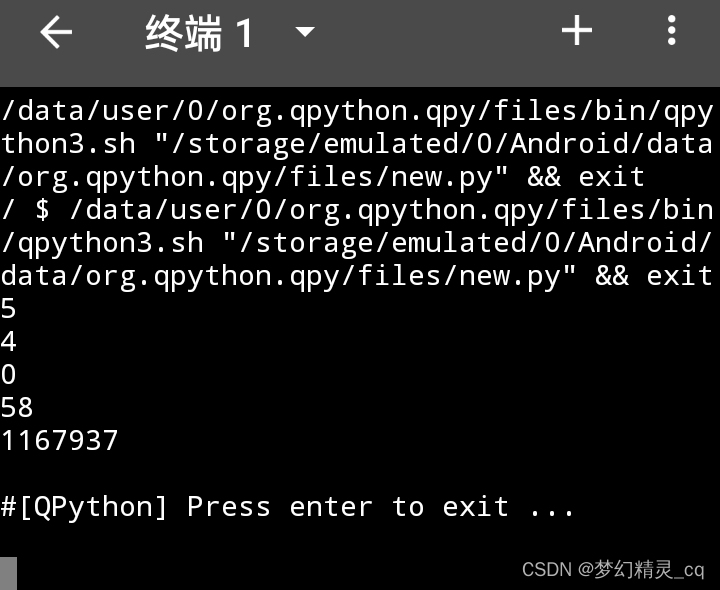
    在这里插入图片描述
    在这里插入图片描述
     
    题目样例输出
    在这里插入图片描述


回页目录

2.1 for嵌套


  用两层for来遍历a、b的所有组合，打印每一种a、b组合的可能方案数，函数返回累加的最后结果。


python代码


def jumps(n, a, b): # 计算所有不同游戏组合函数。a1, b1 = not n%a, not n%b # a、b整除于n的bool型变量count = 2 if a1 and b1 else 1 if a1 or b1 else 0 # 单独用a、b完成游戏组合数。for i in range(1, n//a + 1):for j in range(1, n//b + 1):m = i + jif a*i + b*j == n and j:less = min((i, j))count2 = comCount(i+j, less)count += count2return count


回页目录

2.2 遍历优化


  组合方案中，a、b的数量有“b的数量 = a、b总量 - a的数量”的关系。所以，可以用这个关系去除嵌套的内层for，提升代码效率。


python代码


def jumps(n, a, b): # 计算所有不同游戏组合函数。#print(f"\nn, a, b = {n}, {a}, {b}\n\n计算过程：")a1, b1 = not n%a, not n%bcount = 2 if a1 and b1 else 1 if a1 or b1 else 0 # 单独用a、b完成游戏的方。k = 1for i in range(1, n//a + 1):j = (n - a*i)//bm = i + jif a*i + b*j == n and j:less = min((i, j))count2 = comCount(i+j, less)#print(f"\n{k}、{a}×{i} + {b}×{j} = {n}\n{'':>3}{i+j}个位置中取{less}个，有{count2}种组合")k += 1count += count2return count


回页目录


2.3 求a、b中较少者在a、b总数量中的组合数


  求a、b中较少者在a、b总数量中的组合数。为什么是求a、b中数量小者总数量？因为在一定范围内取值组合数量，是一次取值数量越小越多。数量大者，组合少，且与较小数量组合重复，所以只取大的就好。
 
如：4, 1, 2
12 + 21 = 4
从3个位置中取1个有三种，可以是任何一个位置；取2有也三种要么1、3，要么2、3，要么1、2。a的位置变化会，引起b的变化，所以只计算较小者组合数量。


不同组合单行匿名函数


comCount = lambda n,m: len(list(combinations([0]*n, m))) # 求不同组合单行匿名函数。

求a、b中较少者在a、b总数量中的组合数

for i in range(1, n//a + 1):j = (n - a*i)//bm = i + jif a*i + b*j == n and j:less = min((i, j))count2 = comCount(i+j, less)


回页目录

3、完整源码

(源码较长，点此跳过源码)

#!/sur/bin/nve python
# coding: utf-8
from itertools import combinationscomCount = lambda n,m: len(list(combinations([0]*n, m))) # 求不同组合单行匿名函数。def jumps(n, a, b): # 计算所有不同游戏组合函数。#print(f"\nn, a, b = {n}, {a}, {b}\n\n计算过程：")a1, b1 = not n%a, not n%bcount = 2 if a1 and b1 else 1 if a1 or b1 else 0 # 单独用a、b完成游戏的方。k = 1for i in range(1, n//a + 1):j = (n - a*i)//bm = i + jif a*i + b*j == n and j:less = min((i, j))count2 = comCount(i+j, less)#print(f"\n{k}、{a}×{i} + {b}×{j} = {n}\n{'':>3}{i+j}个位置中取{less}个，有{count2}种组合")k += 1count += count2return countif __name__  == "__main__":print(jumps(4, 1, 2))print(jumps(8, 2, 3))print(jumps(11, 6, 7))print(jumps(30, 3, 5))print(jumps(100, 4, 5))#n, a, b, result = 4, 1, 2, 5#n, a, b, result = 8, 2, 3, 4#n, a, b, result = 11, 6, 7, 0#n, a, b, result = 30, 3, 5, 58#n, a, b, result = 100, 4, 5, 1167937#print(f"\n预期输出：{result}\n实际输出：{jumps(n, a, b)}")
回页首

上一篇：  类属性修改(为什么python类不具备被赋值能力？，用魔术方法收集实参，在类中可以定义方法处理实际参数，实现对类“赋值”)
下一篇： 

我的HOT博：

  本次共计收集 246 篇博文笔记信息，总阅读量 40.46w，平均阅读量 1644。已生成 16 篇阅读量不小于 4000 的博文笔记索引链接。数据采集于 2023-10-12 05:41:03 完成，用时 4 分 41.10 秒。

  1. ChatGPT国内镜像站初体验：聊天、Python代码生成等
    ( 59262 阅读)
    博文地址：https://blog.csdn.net/m0_57158496/article/details/129035387
    点赞：126   踩 ：0  收藏：798  打赏：0  评论：71
    本篇博文笔记于 2023-02-14 23:46:33 首发，最晚于 2023-07-03 05:50:55 修改。
  2. 让QQ群昵称色变的神奇代码
    ( 58086 阅读)
    博文地址：https://blog.csdn.net/m0_57158496/article/details/122566500
    点赞：24   踩 ：0  收藏：83  打赏：0  评论：17
    本篇博文笔记于 2022-01-18 19:15:08 首发，最晚于 2022-01-20 07:56:47 修改。
  3. pandas 数据类型之 DataFrame
    ( 9173 阅读)
    博文地址：https://blog.csdn.net/m0_57158496/article/details/124525814
    点赞：6   踩 ：0  收藏：31  打赏：0  评论：0
    本篇博文笔记于 2022-05-01 13:20:17 首发，最晚于 2022-05-08 08:46:13 修改。
  4. 个人信息提取(字符串)
    ( 7215 阅读)
    博文地址：https://blog.csdn.net/m0_57158496/article/details/124244618
    点赞：1   踩 ：0  收藏：13  打赏：0  评论：0
    本篇博文笔记于 2022-04-18 11:07:12 首发，最晚于 2022-04-20 13:17:54 修改。
  5. Python列表(list)反序(降序)的7种实现方式
    ( 7161 阅读)
    博文地址：https://blog.csdn.net/m0_57158496/article/details/128271700
    点赞：5   踩 ：0  收藏：22  打赏：0  评论：8
    本篇博文笔记于 2022-12-11 23:54:15 首发，最晚于 2023-03-20 18:13:55 修改。
  6. 罗马数字转换器|罗马数字生成器
    ( 7035 阅读)
    博文地址：https://blog.csdn.net/m0_57158496/article/details/122592047
    点赞：0   踩 ：0  收藏：1  打赏：0  评论：0
    本篇博文笔记于 2022-01-19 23:26:42 首发，最晚于 2022-01-21 18:37:46 修改。
  7. Python字符串居中显示
    ( 6966 阅读)
    博文地址：https://blog.csdn.net/m0_57158496/article/details/122163023
    点赞：1   踩 ：0  收藏：7  打赏：0  评论：1
    本篇博文笔记
  8. 斐波那契数列的递归实现和for实现
    ( 5523 阅读)
    博文地址：https://blog.csdn.net/m0_57158496/article/details/122355295
    点赞：4   踩 ：0  收藏：2  打赏：0  评论：8
    本篇博文笔记
  9. python清屏
    ( 5108 阅读)
    博文地址：https://blog.csdn.net/m0_57158496/article/details/120762101
    点赞：0   踩 ：0  收藏：8  打赏：0  评论：0
    本篇博文笔记
  10. 练习：字符串统计(坑：f‘string‘报错)
    ( 5103 阅读)
    博文地址：https://blog.csdn.net/m0_57158496/article/details/121723096
    点赞：0   踩 ：0  收藏：1  打赏：0  评论：0
    本篇博文笔记
  11. 回车符、换行符和回车换行符
    ( 5093 阅读)
    博文地址：https://blog.csdn.net/m0_57158496/article/details/123109488
    点赞：1   踩 ：0  收藏：2  打赏：0  评论：0
    本篇博文笔记于 2022-02-24 13:10:02 首发，最晚于 2022-02-25 20:07:40 修改。
  12. 练习：尼姆游戏(聪明版/傻瓜式•人机对战)
    ( 4943 阅读)
    博文地址：https://blog.csdn.net/m0_57158496/article/details/121645399
    点赞：14   踩 ：0  收藏：42  打赏：0  评论：0
    本篇博文笔记
  13. 密码强度检测器
    ( 4323 阅读)
    博文地址：https://blog.csdn.net/m0_57158496/article/details/121739694
    点赞：1   踩 ：0  收藏：4  打赏：0  评论：0
    本篇博文笔记于 2021-12-06 09:08:25 首发，最晚于 2022-11-27 09:39:39 修改。
  14. 练习：生成100个随机正整数
    ( 4274 阅读)
    博文地址：https://blog.csdn.net/m0_57158496/article/details/122558220
    点赞：1   踩 ：0  收藏：6  打赏：0  评论：0
    本篇博文笔记于 2022-01-18 13:31:36 首发，最晚于 2022-01-20 07:58:12 修改。
  15. 我的 Python.color() (Python 色彩打印控制)
    ( 4159 阅读)
    博文地址：https://blog.csdn.net/m0_57158496/article/details/123194259
    点赞：2   踩 ：0  收藏：8  打赏：0  评论：0
    本篇博文笔记于 2022-02-28 22:46:21 首发，最晚于 2022-03-03 10:30:03 修改。
  16. 罗马数字转换器(用罗马数字构造元素的值取模实现)
    ( 4149 阅读)
    博文地址：https://blog.csdn.net/m0_57158496/article/details/122608526
    点赞：0   踩 ：0  收藏：0  打赏：0  评论：0
    本篇博文笔记于 2022-01-20 19:38:12 首发，最晚于 2022-01-21 18:32:02 修改。
推荐条件 阅读量突破四千
(更多热博，请点击蓝色文字跳转翻阅)
回页首

老齐漫画头像

精品文章：

  • 好文力荐：齐伟书稿 《python 完全自学教程》 Free连载(已完稿并集结成书，还有PDF版本百度网盘永久分享，点击跳转免费🆓下载。)
  • OPP三大特性：封装中的property
  • 通过内置对象理解python'
  • 正则表达式
  • python中“*”的作用
  • Python 完全自学手册
  • 海象运算符
  • Python中的 `!=`与`is not`不同
  • 学习编程的正确方法

来源：老齐教室

◆ Python 入门指南【Python 3.6.3】

好文力荐：

  • 全栈领域优质创作者——[寒佬](还是国内某高校学生)博文“非技术文—关于英语和如何正确的提问”，“英语”和“会提问”是编程学习的两大利器。
  • 【8大编程语言的适用领域】先别着急选语言学编程，先看它们能干嘛
  • 靠谱程序员的好习惯
  • 大佬帅地的优质好文“函数功能、结束条件、函数等价式”三大要素让您认清递归

CSDN实用技巧博文：

  • 8个好用到爆的Python实用技巧
  • python忽略警告
  • Python代码编写规范
  • Python的docstring规范（说明文档的规范写法）

这篇关于跳台阶游戏(Python排列组合函数itertools.combinations的应用)的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/406599。

相关文章

使用Python和OpenCV库实现实时颜色识别系统

使用Python和OpenCV库实现实时颜色识别系统

《使用Python和OpenCV库实现实时颜色识别系统》：本文主要介绍使用Python和OpenCV库实现的实时颜色识别系统,这个系统能够通过摄像头捕捉视频流,并在视频中指定区域内识别主要颜色（红... 目录一、引言二、系统概述三、代码解析1. 导入库2. 颜色识别函数3. 主程序循环四、HSV色彩空间详解
阅读更多...
一文深入详解Python的secrets模块

一文深入详解Python的secrets模块

《一文深入详解Python的secrets模块》在构建涉及用户身份认证、权限管理、加密通信等系统时,开发者最不能忽视的一个问题就是“安全性”,Python在3.6版本中引入了专门面向安全用途的secr... 目录引言一、背景与动机：为什么需要 secrets 模块？二、secrets 模块的核心功能1. 基
阅读更多...
python常见环境管理工具超全解析

python常见环境管理工具超全解析

《python常见环境管理工具超全解析》在Python开发中,管理多个项目及其依赖项通常是一个挑战,下面：本文主要介绍python常见环境管理工具的相关资料,文中通过代码介绍的非常详细,需要的朋友... 目录1. conda2. pip3. uvuv 工具自动创建和管理环境的特点4. setup.py5.
阅读更多...
Python常用命令提示符使用方法详解

Python常用命令提示符使用方法详解

《Python常用命令提示符使用方法详解》在学习python的过程中,我们需要用到命令提示符(CMD)进行环境的配置,：本文主要介绍Python常用命令提示符使用方法的相关资料,文中通过代码介绍的... 目录一、python环境基础命令【Windows】1、检查Python是否安装2、 查看Python的安
阅读更多...
Python UV安装、升级、卸载详细步骤记录

Python UV安装、升级、卸载详细步骤记录

《PythonUV安装、升级、卸载详细步骤记录》：本文主要介绍PythonUV安装、升级、卸载的详细步骤,uv是Astral推出的下一代Python包与项目管理器,主打单一可执行文件、极致性能... 目录安装检查升级设置自动补全卸载UV 命令总结 官方文档详见：https://docs.astral.sh/
阅读更多...
Python并行处理实战之如何使用ProcessPoolExecutor加速计算

Python并行处理实战之如何使用ProcessPoolExecutor加速计算

《Python并行处理实战之如何使用ProcessPoolExecutor加速计算》Python提供了多种并行处理的方式,其中concurrent.futures模块的ProcessPoolExecu... 目录简介完整代码示例代码解释1. 导入必要的模块2. 定义处理函数3. 主函数4. 生成数字列表5.
阅读更多...
Python中help()和dir()函数的使用

Python中help()和dir()函数的使用

《Python中help()和dir()函数的使用》我们经常需要查看某个对象（如模块、类、函数等）的属性和方法,Python提供了两个内置函数help()和dir(),它们可以帮助我们快速了解代... 目录1. 引言2. help() 函数2.1 作用2.2 使用方法2.3 示例(1) 查看内置函数的帮助(
阅读更多...
Python虚拟环境与Conda使用指南分享

Python虚拟环境与Conda使用指南分享

《Python虚拟环境与Conda使用指南分享》：本文主要介绍Python虚拟环境与Conda使用指南,具有很好的参考价值,希望对大家有所帮助,如有错误或未考虑完全的地方,望不吝赐教... 目录一、python 虚拟环境概述1.1 什么是虚拟环境1.2 为什么需要虚拟环境二、Python 内置的虚拟环境工具
阅读更多...
Python实例题之pygame开发打飞机游戏实例代码

Python实例题之pygame开发打飞机游戏实例代码

《Python实例题之pygame开发打飞机游戏实例代码》对于python的学习者,能够写出一个飞机大战的程序代码,是不是感觉到非常的开心,：本文主要介绍Python实例题之pygame开发打飞机... 目录题目pygame-aircraft-game使用 Pygame 开发的打飞机游戏脚本代码解释初始化部
阅读更多...
Python pip下载包及所有依赖到指定文件夹的步骤说明

Python pip下载包及所有依赖到指定文件夹的步骤说明

《Pythonpip下载包及所有依赖到指定文件夹的步骤说明》为了方便开发和部署,我们常常需要将Python项目所依赖的第三方包导出到本地文件夹中,：本文主要介绍Pythonpip下载包及所有依... 目录步骤说明命令格式示例参数说明离线安装方法注意事项总结要使用pip下载包及其所有依赖到指定文件夹，请按照以
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2