多目标遗传算法M0GA（从Pareto非劣等解决方案中选择最优解）

解决多目标优化问题可以分为三大类：

• 函数关系法：寻找目标之间的函数关系，以转化为单一目标问题
• 非支配关系法：通过非支配关系找到pareto解
• 评价因子法：根据偏好增加评价系统

一些常见的方法包括：

• 拓扑 ：通过与理想解的相似性进行排序的技术
• 模糊逻辑
• 无监督ML：自动提取数学关系

所有的方法都有一个共同点，即在优化目标的基础上引入附加的条件。解决mop问题的关键在于正确地指导损益。
要选择最优解决方法，其规则如下：

• 最大收益比（绩效/价格）
• 为目标分配优先级顺序

该方法基于性能-价格比，仅对一个双目标问题进行了验证

概念

多目标遗传算法: h个变量, r 个多目标函数和 n个约束

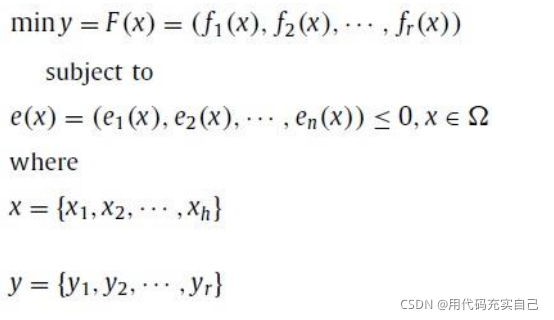
Xf是可行区域，x是该区域的解。因此，不存在x′使得F（x’）优于F（x），即F（x’）>F（x）。只有这样，x才是非劣的Xf中的解决方案。Xf是可行区域，x是该区域的解。因此，不存在x′使得F（x’）优于
F（x），即F（x’）>F（x）。只有这样，x才是非劣的Xf中的解决方案。

• 帕累托前沿的特征： 假设在非劣帕累托前沿有M个解。它们按的值按升序排序，目标f1和f1的标记范围为1到M。

  • 最大-最小/最小-最大模型：如果f1m在增加，f2m也在增加。
    
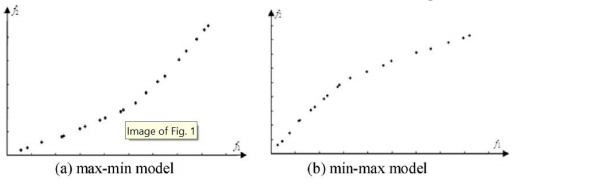
  • 最小-最小/最大-最大模型：如果为f1m增大，f2m减小。
    我们可以从以下模型推断，连接任意两个点的一条线对于最小-最大模型具有正斜率，对于最大-最大模型具有负斜率。

• 平均可变性：连接两条相邻线路的坡度的平均值端点以外的点。
  

• 灵敏度比：平均变量与其各自目标函数值的比率
  

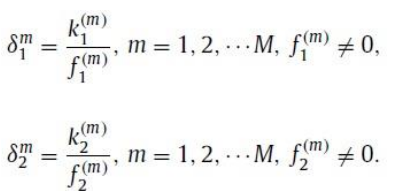
• 灵敏度比的无量纲化：
  

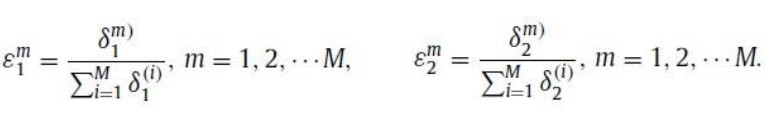
• 支配关系：现在我们有了灵敏度比，我们可以基于它创建一个pareto子集，名为X*。Xi中的元素席是xx*中没有xJ的，其中E1j> E1i和E2j> E2i。

• 偏差度/权重:对于不同的目标函数，解的偏差度是（0，1）中的值。它可用于以后根据偏好选择解决方案，方法是参考其对不同目标的偏差程度
  
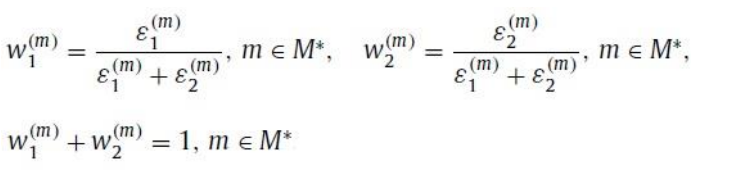
  目标在性质上可能相互冲突，因此增加一个目标的权重可能导致另一个目标的权重降低。

• 好的解决方案：基于上述分析，使用以下标准选择一个好的解决方案
  
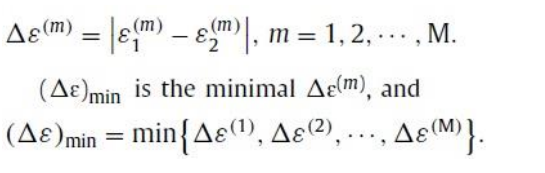
  最小值为的解△Emin被认为是无偏的或好的解决方案。实际上，一个好的解决方案对于两个目标函数都有很高的性能价格比

流程图：

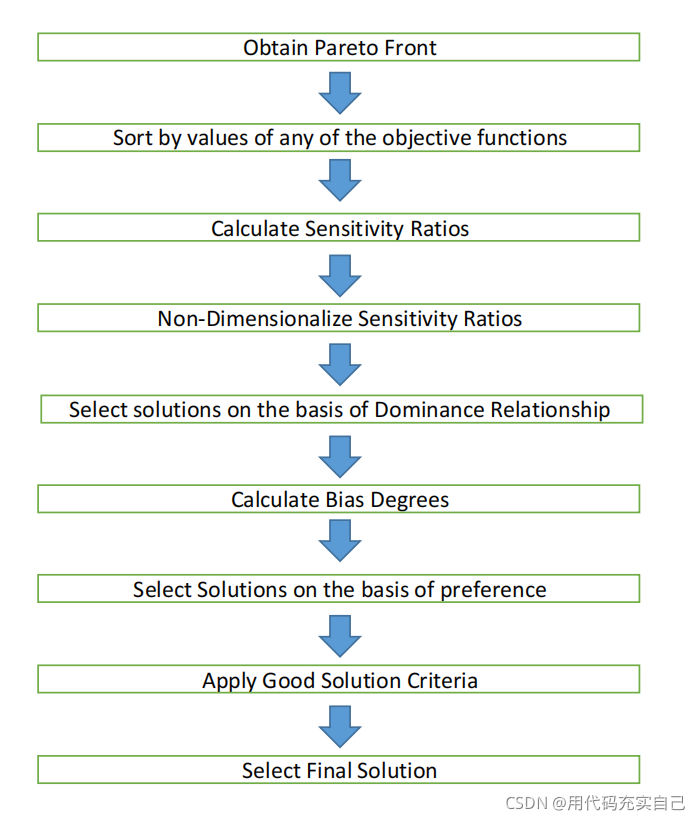
结论

上述方法减少了集合中非劣解的数量。它是决策者获得最优解的一种定量方法。如果所有目标都被同等地考虑，则可以根据性能价格比得到一个好的解决方案。