交换排序详讲：冒泡排序+快速排序+快排优化+非递归实现（多方法+思路+图解+代码）

2023-11-21 09:52
文章标签 代码 实现 方法 优化 快速 排序 图解 交换 递归 冒泡排序 快排 思路 详讲

本文主要是介绍交换排序详讲：冒泡排序+快速排序+快排优化+非递归实现（多方法+思路+图解+代码），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

文章目录

  • 交换排序
      • 一.冒泡排序
      • 二.快速排序
          • 1.挖坑法
          • 2.Hoare法
          • 3.前后指针法
          • 4.快速排序的优化
            • 方法一：随机选取基准值
            • 方法二：三数取中法选基准值
            • 方法三：递归到最小区间时、用插入排序
          • 5.快速排序非递归实现

交换排序

  • 根据序列中两个记录键值的比较结果来对换这两个记录在序列中的位置
  • 将键值较大的记录向序列的尾部移动，键值较小的记录向序列的前部移动。

一.冒泡排序

在这里插入图片描述

    /*** 冒泡排序* 时间复杂度 n^2* 空间复杂度  1* @param array*/public static void bubbleSort(int[]array){for (int i = 0; i < array.length-1; i++) {//趟数boolean flg =false;for (int j = 0; j < array.length-1-i; j++) {if (array[j]>array[j+1]){swap(array,j,j+1);flg = true;}}if (flg == false){return;}}}

1.遍历 i 代表交换的趟数，遍历 j 进行两两交换

2.j < array.length-1-i 是对于趟数的优化，每走一趟，交换就少一次

3.boolean flg =false;当两两交换时，flg变为true

4.进一步优化：如果遍历完，没发生交换，flg还是false,直接返回，排序结束

  • 时间复杂度：O ( N2 )
  • 空间复杂度：O ( 1 )
  • 稳定性：稳定

二.快速排序

  • 二叉树结构的交换排序方法

  • 任取一个待排序元素作为基准值，把序列一分为二，左子序都比基准值小，右子序都比基准值大，左右两边再重复进行

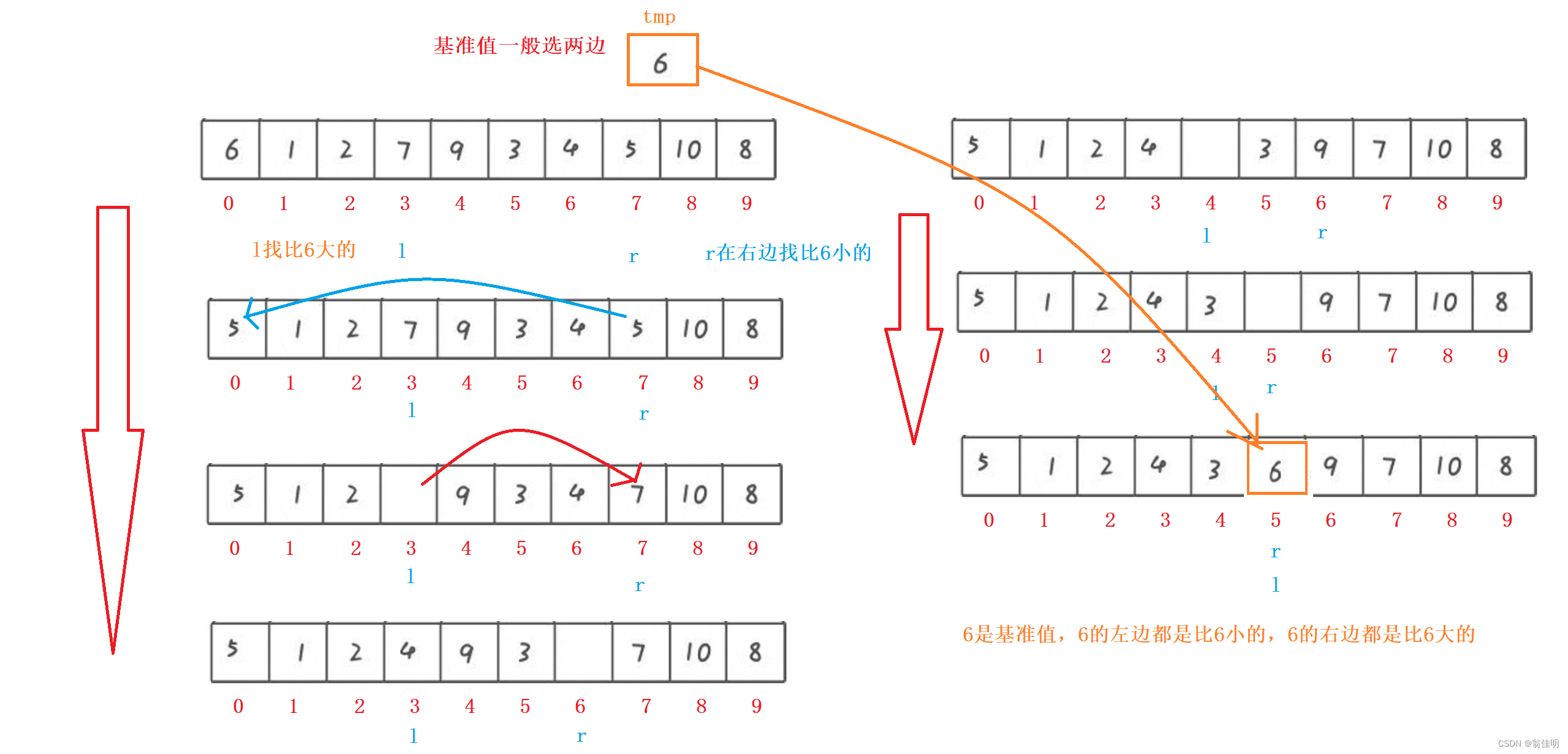
在这里插入图片描述

  • 左边找比基准值大的，右边找比基准值小的
1.挖坑法

在这里插入图片描述

  • 基准值位置挖一个坑，后面找一个比基准值小的把坑埋上
  • 前面找一个比基准值大的，埋后面的坑
  • 当l==r时，把基准值填入剩下的坑中

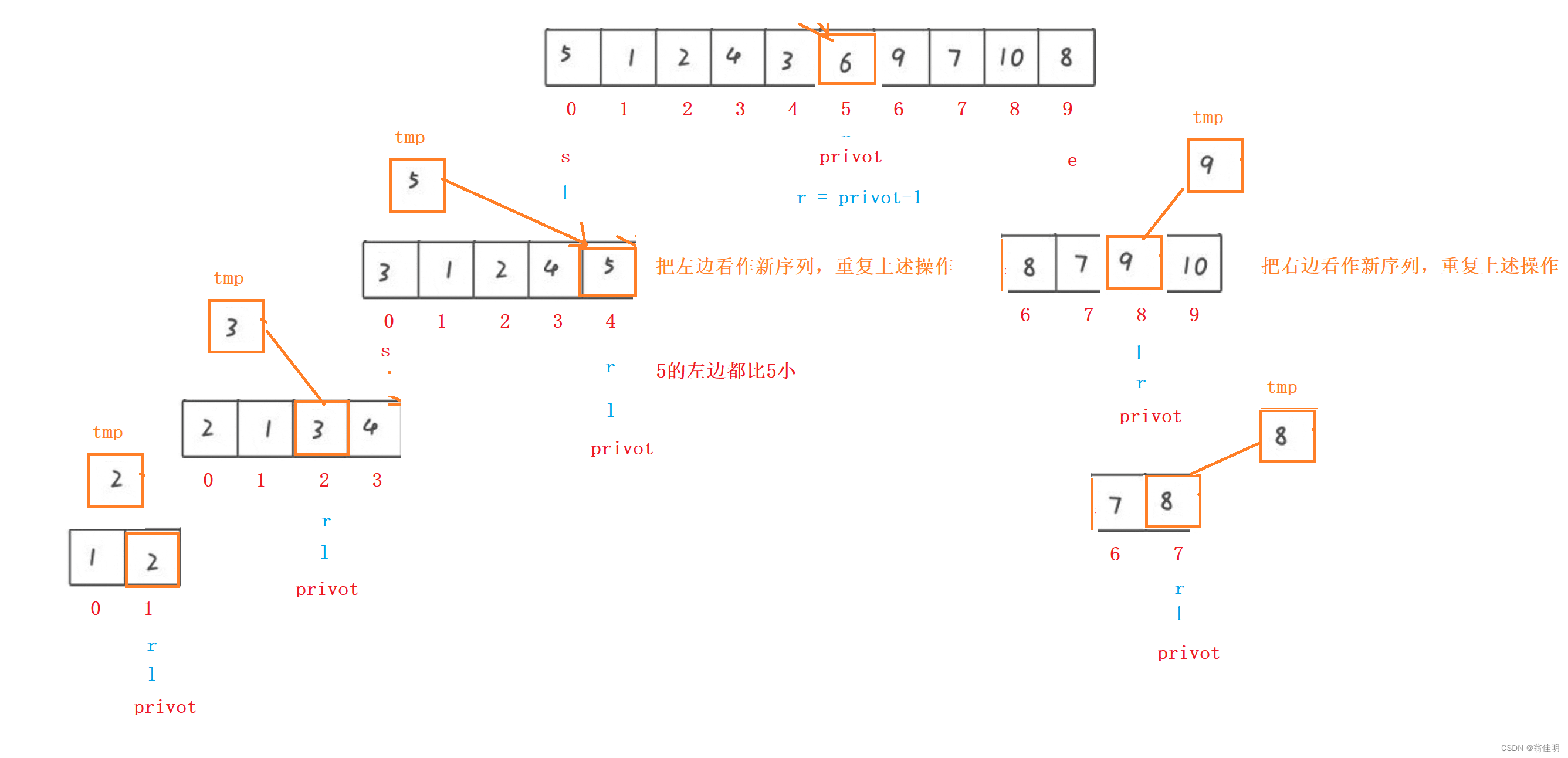
在这里插入图片描述

  • 左右两边重复进行上述步骤，直到排完为止
  • 左右两边都以同样的方法进行划分，运用递归来实现
    /*** 快速排序 ---挖坑法** @param array*/public static void quickSort(int[] array) {quick(array, 0, array.length - 1);}private static void quick(int[] array, int start, int end) {if (start >= end) {return;//结束条件// start == end，说明只剩一个了，是有序的，返回//start > end ,说明此时的基准值在开头或者末尾//在开头：start不变，end=pivot-1,start > end ，end=-1 没有左树//在结尾：end不变，start = pivot+1,start > end,超出索引，没有右树}//不断递归quickint pivot = partition(array, start, end);// 进行排序，划分找到pivot//然后递归划分法左边，递归划分的右边quick(array, start, pivot - 1);quick(array, pivot + 1, end);}//划分，返回基准值private static int partition(int[] array, int left, int right) {int tmp = array[left];//挖一个坑，取left位置为基准值while (left < right) {//在右边找一个比基准值小的把坑填上while (left < right && array[right] >= tmp) {//防止越界right--;}array[left] = array[right];//找到比tmp小的数，填坑,//在左边找一个比tmp大的值，填到右边的坑while (left < right && array[left] <= tmp) {//防止越界left++;}array[right] = array[left];}//如果相遇了，退出循环array[left] = tmp;//填坑return left;}

  • 先划分序列，递归左边，然后再递归右边

  • 递归结束条件：

    start == end时，说明只剩一个了，是有序的，返回
    start > end 时 ,说明此时的基准值在开头或者末尾

    如果基准值在开头：start不变，end=pivot-1,start > end ，end=-1 没有左树
    如果基准值在结尾：end不变，start = pivot+1,start > end,超出索引，没有右树

2.Hoare法

在这里插入图片描述

  • 不同的方法，找出基准值，排的序列是不一样的

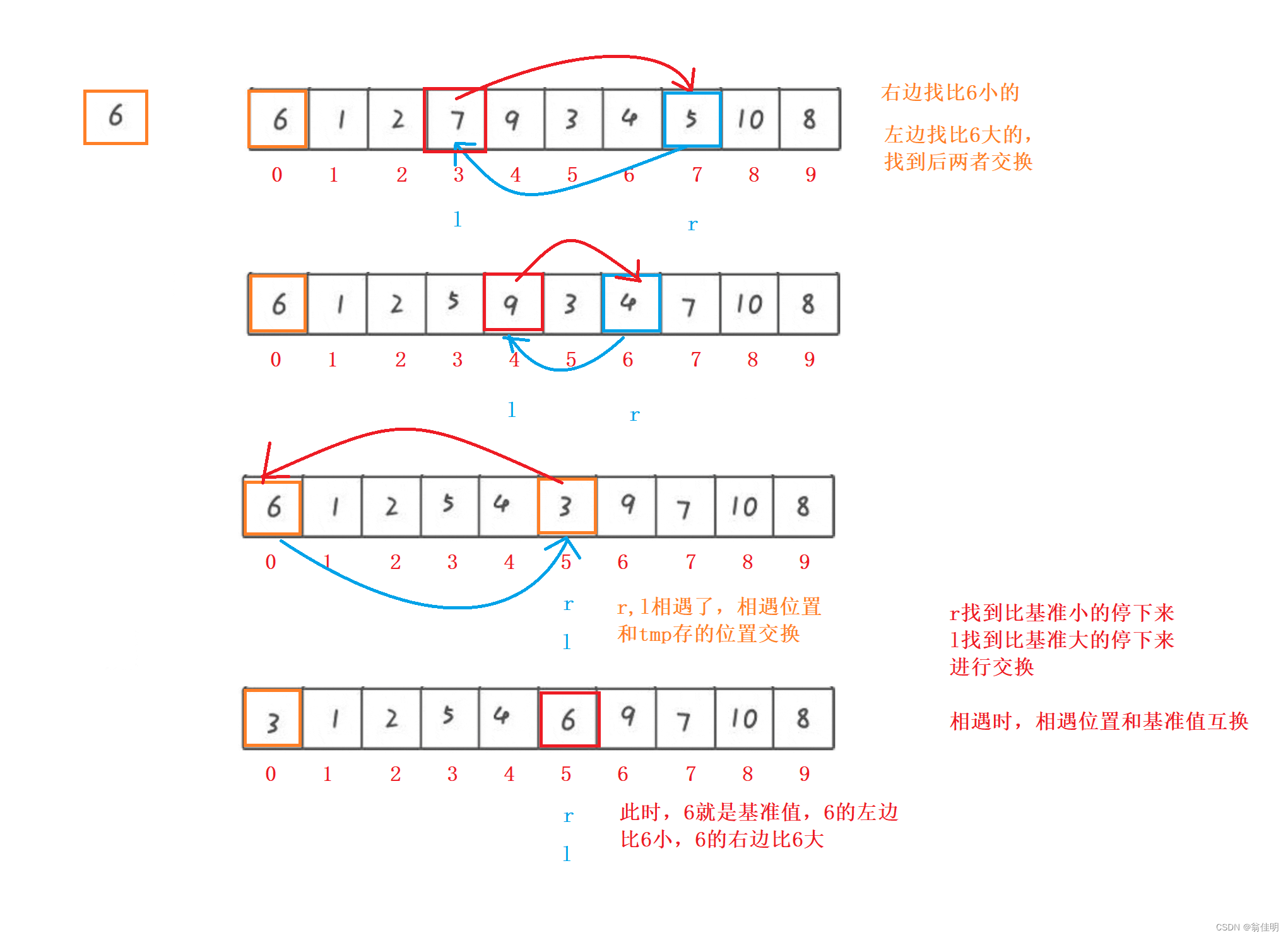
在这里插入图片描述

  • i记录基准值一开始在left位置的下标
  • r找到比基准值小的停下来，l找到比基准值大的停下来，互相交换
  • l和r相遇的时候，把i 记录基准值的初始下标和相遇位置交换

以左边为基准，先找右边再找左边，相遇的位置就是以右边为基准的值，要比基准小，才能交换

    /*** Hoare法 划分排序找基准值* @param array* @param left* @param right* @return*/private static int partition2(int[] array, int left, int right) {int tmp = array[left];int i  = left;//记录基准值一开始在left位置的下标while (left < right) {while (left < right && array[right] >= tmp) {right--;}while (left < right && array[left] <= tmp) {left++;}swap(array,left,right);}swap(array,i,left);return left;}
3.前后指针法

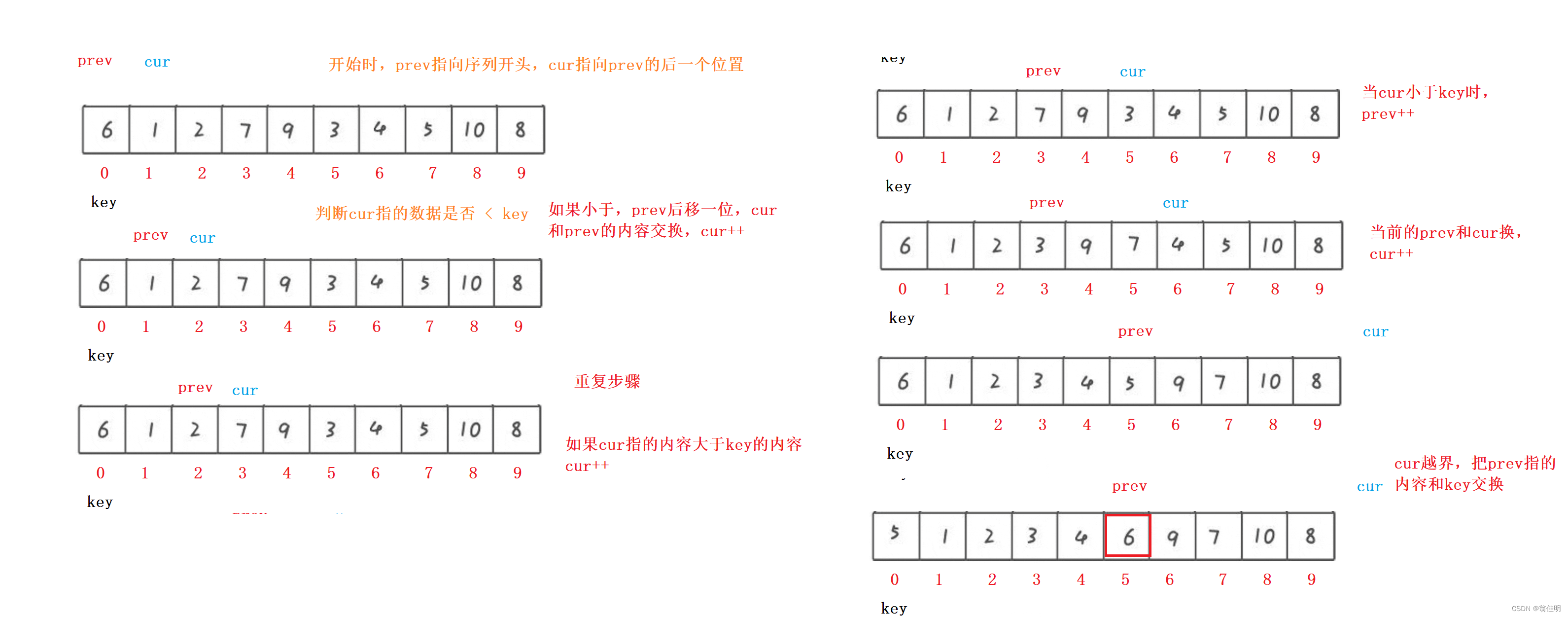
在这里插入图片描述

在这里插入图片描述

  • prev记录了比key小的最后一个位置
  • cur去找比key值小的，找到后，放到prev的下一个位置
  • 最后找到基准值，并且基准值的左边都比它小，右边都比他大
    /*** 前后指针法，划分排序找基准值** @param array* @param left* @param right* @return*/private static int partition3(int[] array, int left, int right) {int prev = left; //prev从left位置开始，left为当前的基准值int cur = left + 1;//cur在prev的后一个while (cur <= right) {//遍历完当前数组段if (array[cur] < array[left] && array[++prev] != array[cur]) {//只要cur指向的值小于left位置的基准值//并且prev++后不等于cur的值swap(array, cur, prev);//将cur和prev位置的值交换//cur++;}//如果cur的值大于基准值,或者prev下一位的值等于cur,cur后移cur++;}//cur越界，循环结束，最后，交换基准值和prev位置的值//prev记录的就是比基准值小的最后一个数swap(array, prev, left);return prev;//prev为基准值}
4.快速排序的优化

  • 时间复杂度：

    最好情况：O (N*log2N) ：树的高度为log2N，每一层都是N

    最坏情况:O (N2)：有序、逆序的情况下,没有左树，只有右树，单分支树，树的高度是N,每一层都是N

  • 空间复杂的：

    最好情况：O (log2N)：满二叉树（均匀分割待排序的序列，效率最高）树高为 log2N

    最坏情况：O（N）:单分支树,树高为N

  • 稳定性：不稳定

  • 快速排序有可能发生栈溢出异常，需要进行优化

  • 所以要能均匀分割待排序的序列

递归的次数多了，会导致栈溢出，所以优化的方向就是减少递归的次数

在最坏情况下，比如顺序，基准值都取自左边，本身没有左树

方法一：随机选取基准值

看人品，有概率

方法二：三数取中法选基准值

三数：第一个数、中间的数、最后一个数 ，在这三个数中，选出中等值

有可能会变成二分查找 ，避免了出现最坏情况，从中值来比较排序，左右树都有

    public static void quickSort(int[] array) {quick2(array, 0, array.length - 1);}private static void quick2(int[] array, int start, int end) {if (start >= end) {return;//结束条件}//三数取中法int index = midThree(array, start, end);//选出的数和开头交换swap(array,index,start);int pivot = partition(array, start, end);// 进行排序，划分找到pivot//然后递归划分法左边，递归划分的右边quick2(array, start, pivot - 1);quick2(array, pivot + 1, end);}/*** 三数取中* @param array* @param left* @param right* @return*/private static int midThree(int[] array, int left, int right) {int mid = (left + right) / 2;if (array[left] < array[right]) {if (array[mid] < array[left]) {return left;} else if (array[mid] > array[right]) {return right;} else {return mid;}} else {if (array[mid] < array[right]) {return right;} else if (array[mid] > array[left]) {return left;} else {return mid;}}}
方法三：递归到最小区间时、用插入排序

进一步优化：减少递归的次数：

  • 把快排的递归想象成二叉树，最后两层包含了大部分数，我们要减少这部分的递归

  • 前几次的找基准值排序，导致后面几层趋于有序，用直接插入法来排序，进一步提高效率，有点像希尔排序

如果树的高度为h,最后一层就有 2 h-1 个结点 ，后两层占了绝大部分

设置条件：end-start+1 就是当前待排序列的长度，如果小于等于某个较小的值，直接采用插入排序来排剩下的

 private static void quick2(int[] array, int start, int end) {if (start >= end) {return;//结束条件}//优化----减少递归的次数if(end-start+1<=20){//如果当前数列的长度，小于=15的时候，// 用插入排序,然后退出insertSortQ(array,start,end);return;}//三数取中法int index = midThree(array, start, end);swap(array,index,start);int pivot = partition(array, start, end);// 进行排序，划分找到pivot//然后递归划分法左边，递归划分的右边quick2(array, start, pivot - 1);quick2(array, pivot + 1, end);}/*** 插入排序---来排剩下的待排部分，给定需要的区间*/private static void insertSortQ(int[] array,int left,int right) {for (int i = left+1; i <= right; i++) {int tmp = array[i];int j = i - 1;for (; j >= left; j--) {if (array[j] > tmp) {array[j + 1] = array[j];} else {break;}}array[j + 1] = tmp;}}
5.快速排序非递归实现
  • 1.通过使用栈来实现
  • 2.每次找到基准值后，把两段序列的开头和末尾压栈
  • 3.从栈顶取出两个元素作为新序列的首尾，再次找基准值
  • 4.找到基准值后，如果右边有一个元素，不进栈，有两个元素的才能进栈
  • 5.pivot< end-1:证明右边有两个元素，pivot>s+1：证明左边有两个元素
  • 6.栈为空的时候，排完元素
    /*** 非递归实现快速排序** @param array*/public static void quickSortNonRecursive(int[] array) {Deque<Integer> stack = new LinkedList<>();//利用栈来实现int left = 0;int right = array.length - 1;//先找到基准值int pivot = partition(array, left, right);//左边有两个元素时，根据基准值进栈if (pivot > left + 1) {stack.push(left);stack.push(pivot - 1);}//有边有两个元素时，根据基准值进栈if (pivot < right - 1) {stack.push(pivot + 1);stack.push(right);}//栈不为空的时候，取两个栈顶元素做为区间//再次进栈出栈while (!stack.isEmpty()) {right = stack.pop();left = stack.pop();pivot = partition(array, left, right);//左边有两个元素时，根据基准值进栈if (pivot > left + 1) {stack.push(left);stack.push(pivot - 1);}//有边有两个元素时，根据基准值进栈if (pivot < right - 1) {stack.push(pivot + 1);stack.push(right);}}}

点击移步博客主页，欢迎光临~

偷cyk的图

这篇关于交换排序详讲：冒泡排序+快速排序+快排优化+非递归实现（多方法+思路+图解+代码）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/401573。

相关文章

基于 HTML5 Canvas 实现图片旋转与下载功能(完整代码展示)

基于 HTML5 Canvas 实现图片旋转与下载功能(完整代码展示)

《基于HTML5Canvas实现图片旋转与下载功能(完整代码展示)》本文将深入剖析一段基于HTML5Canvas的代码，该代码实现了图片的旋转（90度和180度）以及旋转后图片的下载... 目录一、引言二、html 结构分析三、css 样式分析四、JavaScript 功能实现一、引言在 Web 开发中，
阅读更多...
SpringBoot中使用Flux实现流式返回的方法小结

SpringBoot中使用Flux实现流式返回的方法小结

《SpringBoot中使用Flux实现流式返回的方法小结》文章介绍流式返回（StreamingResponse）在SpringBoot中通过Flux实现,优势包括提升用户体验、降低内存消耗、支持长连... 目录背景流式返回的核心概念与优势1. 提升用户体验2. 降低内存消耗3. 支持长连接与实时通信在Sp
阅读更多...
Conda虚拟环境的复制和迁移的四种方法实现

Conda虚拟环境的复制和迁移的四种方法实现

《Conda虚拟环境的复制和迁移的四种方法实现》本文主要介绍了Conda虚拟环境的复制和迁移的四种方法实现,包括requirements.txt,environment.yml,conda-pack,... 目录在本机复制Conda虚拟环境相同操作系统之间复制环境方法一：requirements.txt方法
阅读更多...
Nginx 重写与重定向配置方法

Nginx 重写与重定向配置方法

《Nginx重写与重定向配置方法》Nginx重写与重定向区别：重写修改路径（客户端无感知）,重定向跳转新URL（客户端感知）,try_files检查文件/目录存在性,return301直接返回永久重... 目录一.try_files指令二.return指令三.rewrite指令区分重写与重定向重写: 请求
阅读更多...
MySQL 打开binlog日志的方法及注意事项

MySQL 打开binlog日志的方法及注意事项

《MySQL打开binlog日志的方法及注意事项》本文给大家介绍MySQL打开binlog日志的方法及注意事项,本文通过实例代码给大家介绍的非常详细,对大家的学习或工作具有一定的参考借鉴价值,需要... 目录一、默认状态二、如何检查 binlog 状态三、如何开启 binlog3.1 临时开启（重启后失效）
阅读更多...
Spring Boot 实现 IP 限流的原理、实践与利弊解析

Spring Boot 实现 IP 限流的原理、实践与利弊解析

《SpringBoot实现IP限流的原理、实践与利弊解析》在SpringBoot中实现IP限流是一种简单而有效的方式来保障系统的稳定性和可用性,本文给大家介绍SpringBoot实现IP限... 目录一、引言二、IP 限流原理2.1 令牌桶算法2.2 漏桶算法三、使用场景3.1 防止恶意攻击3.2 控制资源
阅读更多...
Python如何去除图片干扰代码示例

Python如何去除图片干扰代码示例

《Python如何去除图片干扰代码示例》图片降噪是一个广泛应用于图像处理的技术,可以提高图像质量和相关应用的效果,：本文主要介绍Python如何去除图片干扰的相关资料,文中通过代码介绍的非常详细,... 目录一、噪声去除1. 高斯噪声（像素值正态分布扰动）2. 椒盐噪声（随机黑白像素点）3. 复杂噪声（如伪
阅读更多...
springboot下载接口限速功能实现

springboot下载接口限速功能实现

《springboot下载接口限速功能实现》通过Redis统计并发数动态调整每个用户带宽,核心逻辑为每秒读取并发送限定数据量,防止单用户占用过多资源,确保整体下载均衡且高效,本文给大家介绍spring... 目录 一、整体目标 二、涉及的主要类/方法✅ 三、核心流程图解（简化） 四、关键代码详解1️⃣ 设置
阅读更多...
Java Spring ApplicationEvent 代码示例解析

Java Spring ApplicationEvent 代码示例解析

《JavaSpringApplicationEvent代码示例解析》本文解析了Spring事件机制,涵盖核心概念（发布-订阅/观察者模式）、代码实现（事件定义、发布、监听）及高级应用（异步处理、... 目录一、Spring 事件机制核心概念1. 事件驱动架构模型2. 核心组件二、代码示例解析1. 事件定义
阅读更多...
Nginx 配置跨域的实现及常见问题解决

Nginx 配置跨域的实现及常见问题解决

《Nginx配置跨域的实现及常见问题解决》本文主要介绍了Nginx配置跨域的实现及常见问题解决,文中通过示例代码介绍的非常详细,对大家的学习或者工作具有一定的参考学习价值,需要的朋友们下面随着小编来... 目录1. 跨域1.1 同源策略1.2 跨域资源共享（CORS）2. Nginx 配置跨域的场景2.1
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2