进化算法——生物地理学

生物地理学这门科学可以追溯到19世纪最著名的自然学家阿尔弗雷德·华莱士和查尔斯·达尔文的工作。人们通常认为华莱士是生物地理学之父。

生物地理学的数学模型描述物种形成（新物种的进化），物种在岛屿之间的迁徙，以及物种的灭绝。一个岛屿是指任何一个栖息地，它在地理上与其他栖息地隔离。

益于生物生存的地理区域可以说具有高的生境适宜度指数（HSI）。与HSI相关的特征包括像降雨量、植物多样性、地形多向性、土地面积以及温度等因素。这些特征被称为适应度指数变量（SIVs）。

HSI高的岛屿适合各种各样的物种，在HSI低的岛屿上则只有几种物种可以生存。由于HSI高的岛屿上生存着大量的生物，有很多物种会从HSI高的岛屿迁徙到附近的栖息地。在用生物地理学开发BBO（生物地理学优化）时假定一个物种从一个岛迁出则该物种在岛上灭绝。

HSI高的岛屿有高迁出入以及低迁入率，HSI低的岛屿则有着高的迁入率。如下图所示：

物种多样性与HSI有关，来到HSI低的岛屿的物种越多，这个岛的HSI增大的机会就越大。上图说明在单个岛上物种丰富程度的模型。迁入率和迁出率随着岛上的物种数变化。上图的迁移曲线是直线，一般要比这复杂。

当岛上物种为0时，迁到这个岛上栖息的迁入率最大，记为I。栖息地能支撑的最大物种数量是。如果岛上没有物种，则迁出率为0，当岛上物种增加，变得拥挤就会有更多的物种离开，迁出率增加。当岛上物种达到它能支撑的最大值，迁出率达到最大，记为E。

目录

生物地理学是一个优化的过程

基于生物地理学的优化

BBO的扩展 

BBO与遗传算法

生物地理学是一个优化的过程

生物地理学是种群分布的一种自然方式，人们常常把它看作为在栖息地维持均衡的过程来研究。在生物地理学中，稳定性和最优性是一个硬币的两面。生物地理学中的最优性涉及能高度适应其环境的多样的复杂的群体。生物地理学中的稳定性涉及已有种群的持久性。复杂的群体比简单的群体适应性更强。

人们普遍人同最优性和稳定性之间的互补特征。均衡和最优不过是对同一现象的不同看法。

生物地理学是一个正反馈现象，它类似于自然选择，适者生存。

基于生物地理学的优化

假设有一个优化问题和一些候选解，称候选解为个体。好的个体在问题上的表现好，差的个体在问题上表现差。好的个体类似于高HSI的岛屿，差的个体类似于低HSI的岛屿。宜居的岛屿迁入率比不太宜居的岛屿迁入率低，好的个体比差的个体更抗拒改变。好的个体易于与差的个体分享好的个体的特征，不太宜居的岛屿更有可能接受来自宜居岛屿的很多移民。新特征的加入可能会提高差的个体的质量。基于这个方法的进化算法被称为基于生物地理学优化（BBO）。

假定每一个BBO个体都由完全相同的物种数的曲线表示，如下图。S1代表一个较差的个体，S2代表一个较好的个体。对于S1迁入率较高，这意味着它有可能接受来自别的候选解的新特征。对于S2迁出率较高，这意味着它有可能与其他个体分享其特征。

 利用每一个个体的迁移率在个体之间以概率分享信息。假设种群规模为N，是种群中的第k个个体，优化问题的维数为n，是中的第s个独立变量，其中k∈[1,N]，s∈[1,n]。在每一代，第k个个体的每一个解的特征，存在被替换的概率为(迁入概率)：对于k∈[1,N]，s∈[1,n]有：

= 中第s个独立变量被替换的概率

如果选出了要被替换的解的特征，我们用与迁出概率{}成正比的概率选出迁出的解。在这一步可以采用任何一种基于适应度的选择方法，如果使用轮盘赌选择则：

由此可以得到下面的算法（标准BBO算法，也称基于部分迁入的BBO算法）。在当前这一代，种群中的个体被替换之前要完成没一个个体的迁移和变异，因此在算法中需要借用临时种群z。

BBO的扩展 

1.迁移曲线

生物地理学中的迁移曲线是非线性的，很难量化生物地理学的迁移曲线的确切形状，不同岛的迁移曲线也不同，但在自然界中有很多曲线呈S型。

非归一化的曲线建模为：

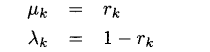
其中是种群中第k个个体的适应度的排名，对于适应性最差的个体， =1，而对于最好的个体，=N（种群规模）。用正弦迁移率建模，迁移率的值设定为：

由上式得到的S型曲线如下图所示：

2.混合迁移

在混合交叉中，子代的基因不再复制父代的单个基因，而是两个父代基因的凸组合。这促使我们在BBO中使用混合迁移算子。在标准BBO算法中，个体的特征全部由个体的特征替换。

在BBO的混合迁移中，个体 的特征不是由个体的特征替换，而是等于和的凸组合：

其中α∈[0,1]，如果α=0，则混合的BBO算法退化为标准的BBO，可见，混合BBO是对标准BBO的推广。混合参数α可以是随机的、确定的或与  和的相对适应度成正比。

混合迁移适合用于连续解特征的问题。

与标准迁移比较，采用混合迁移有两个理由：首先，好的个体不大可能因为迁移而退化，因为在迁移过程中它们最初的特征会有一部分保留下来。其次，差的个体在迁移过程中至少会接受来自好的个体一部分解的特征。

3.BBO其他办法

BBO还有其他的实施方法。不是对每一个解的特征都用检验随机数，而是对一个个体只用一次检验，如果决定迁入，就替换的所有解的特征。可以称之为基于总迁入的BBO。

还可以利用决定是否迁出已知个体的一个特征。只有当决定迁出之后，才用变量{} 在轮盘赌程序中选择迁入地。根据这个思路得到基于迁入的BBO。

将上面的思想组合起来实施会得到4中BBO算法，第一种，基于部分迁入的BBO算法，它是默认的方法。第二种，基于部分迁出的BBO算法。第三种，基于总迁入的BBO算法。第四种，基于中迁出的BBO算法。第2-4中算法如下所示：

BBO与遗传算法

在才用均匀交叉的遗传算法中，每个子代基因都随机的从它的父代中选择。在基因库重组中，所谓的多父代重组和扫描交叉，子代的每个基因也是随机的从它的父代中选择，这时父代的个数大于2。实施全局均匀重组是基因库重组的一种方式，子代基因从其父代随机得选出来，这里父代种群等价于整个遗传算法种群，并根据适应度值随机地选择（如轮盘赌选择）。

如果我们才用全局均匀重组，并对每一个后代的每一个解的特征采用基于适应度的选择，就得到了下面的算法：

其实BBO算法是特殊类型的全局均匀重组遗传算法的一个推广。因为如果不在BBO算法中令，而是对所有k令，则BBO算法就等价于GA/GUR算法。