本文主要是介绍时间序列预测(8) — Informer模型原理,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
0 摘要
1 引言
2 定义
3 方法
3.1 高效的自注意力机制
3.2 稀疏度度量
3.3 ProbSparse稀疏自注意力机制
3.4 Encoder编码器
3.5 Decoder解码
参考视频:Informer原理及代码解析_哔哩哔哩_bilibili
0 摘要
长序列时间序列预测(LSTF)需要模型具有很高的预测能力,即精确的捕捉输出和输入之间长时间依赖关系的能力。Transformer能很好的提高预测精度,然而Transformer存在几个严重问题,二次时间复杂度、高内存使用和编码器-解码器架构的固有限制。为了解决这些问题,Informer设计了一种高效基于Transformer的LSTF模型,具有三个独特特点:
- ProbSparse稀疏自注意机制,其时间复杂度和内存使用为
 ,在序列依赖性对齐方面具有可比性能;
,在序列依赖性对齐方面具有可比性能; - 自注意力提取突出显示主导关注,通过减半级联层输入有效处理极长输入序列;
- 生成式解码器,概念上简单,可以一次性预测长时间序列,而不是逐步方式,大大提高了长序列预测的推断速度。
1 引言
在能源和智能电网管理、经济和金融、以及疾病传播分析等领域,可以利用大量的过去时间序列数据来进行长期预测。然而,现有方法大多设计用于短期问题设置,比如预测48个点或更少。随着序列越来越长,模型的预测精度随之下降。
当解决LSTF问题时,Transformer存在三个重要的局限性:
- 自注意力的二次计算复杂度问题:自注意力机制的原子操作(即点积),导致每层的时间复杂度和内存使用量为
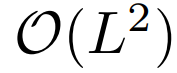 。
。 - 高内存使用量问题:对长序列输入进行堆叠时,J个encoder--decoder层的堆叠使得总内存使用量为
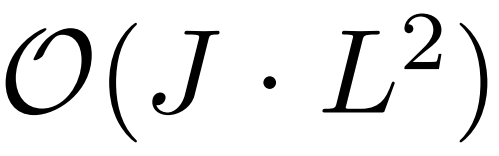 ,这限制了模型在接收长序列输入时的可伸缩性。
,这限制了模型在接收长序列输入时的可伸缩性。 - 预测长输出时速度骤降问题:原始Transformer的动态解码操作导致step by step inference(逐步推理)的速度如同基于RNN的模型一样慢。
逐步推理的含义:只有当前层处理完后才处理下一层,造成模型速度很慢。
Informer深入探讨了这三个问题。研究了自注意力机制中的稀疏性,改进了网络组件。Informer的贡献总结如下:
- 提出了Informer,成功提高了LSTF问题的预测能力,验证了Transformer-like模型捕捉长序列时间序列输出和输入之间个体长程依赖性的潜在价值。
- 提出了ProbSparse稀疏自注意力机制,以有效地替代经典的自注意力。它在依赖对齐上实现了
 的时间复杂度和
的时间复杂度和 的内存使用。
的内存使用。 - 提出了自注意力蒸馏操作,以优先考虑J层堆叠中的主导注意力分数,并将总空间复杂度大幅降至
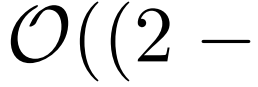
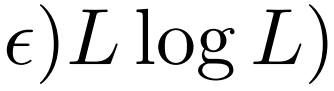 ,有助于接收长序列输入。
,有助于接收长序列输入。 - 提出了生成式解码器,只需进行一次前向步骤即可获得长序列输出,同时避免了推断阶段的累积误差扩散。
2 定义
我们首先提供LSTF问题的定义。在具有固定大小窗口的滚动预测设置下,我们在时间 t :
- 输入:
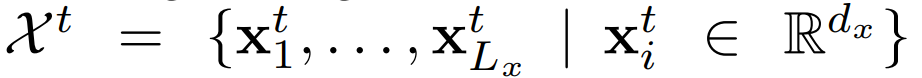
- 输出:
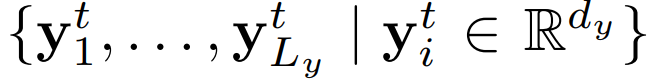 。
。
编码器-解码器架构:将输入表示![]() “编码”为隐藏状态
“编码”为隐藏状态![]() ,并从
,并从![]() “解码”出输出表示
“解码”出输出表示![]() 。流程涉及一个名为“动态解码”的逐步过程,其中解码器从上一步的状态
。流程涉及一个名为“动态解码”的逐步过程,其中解码器从上一步的状态![]() 和来自第 k 步的其他必要输出计算出一个新的隐藏状态
和来自第 k 步的其他必要输出计算出一个新的隐藏状态![]() ,然后预测第(k+1)序列
,然后预测第(k+1)序列![]() 。
。

3 方法
3.1 高效的自注意力机制
经典自注意力是基于元组输入(即查询向量、键向量和值向量)定义的,它执行缩放点积,如
![]()
其中![]() ,
,![]() ,
,![]() 即查询向量、
即查询向量、![]() 键向量、
键向量、![]() 值向量、d为输入维度。
值向量、d为输入维度。
为了进一步讨论自注意力机制,让![]() 分别表示
分别表示![]() 中的第 i 行。按照公式,第 i 个查询的注意力被定义为概率形式的核平滑器:
中的第 i 行。按照公式,第 i 个查询的注意力被定义为概率形式的核平滑器:
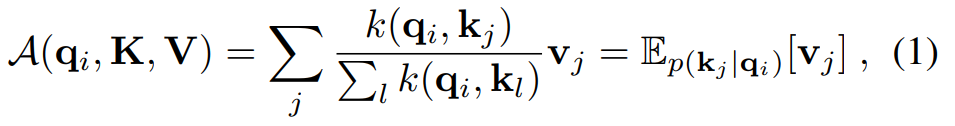
自注意力结合了值并根据计算概率![]() 获取输出。计算复杂度和内存使用为
获取输出。计算复杂度和内存使用为![]() ,并非高效的计算方式。
,并非高效的计算方式。
研究表明,自注意力概率分布具有潜在的稀疏性,并且他们设计了“选择性”计算策略,对所有![]() 进行计数,而不会显著影响性能。
进行计数,而不会显著影响性能。
self-attention的权重构成了一个长尾分布(long tail distribution),也就是很少的权重贡献了主要的attention,而其他的可以被忽略,也就是单前点只与少数历史点相关。
3.2 稀疏度度量
从公式(1)中,第 i 个查询对所有键的注意力定义为概率![]() ,输出是它与值 v 的组合。我们希望该计算的概率分布远离均匀分布。如果
,输出是它与值 v 的组合。我们希望该计算的概率分布远离均匀分布。如果![]() 接近均匀分布,则计算会产生很多冗余,也就是其他点对当前点的影响是一样的,并没有区分度。我们通过Kullback-Leibler散度来测量“相似性”:
接近均匀分布,则计算会产生很多冗余,也就是其他点对当前点的影响是一样的,并没有区分度。我们通过Kullback-Leibler散度来测量“相似性”:
![]()
省略常数,我们定义第 i 个查询的稀疏度量为:
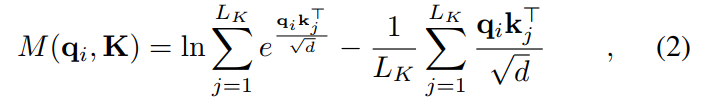
其中第一项是![]() 在所有键上的Log-Sum-Exp(LSE),第二项是它们的算术平均值。如果第 i 个查询获得更大的
在所有键上的Log-Sum-Exp(LSE),第二项是它们的算术平均值。如果第 i 个查询获得更大的![]() ,它的注意力概率 p 更“波动”,也就是更加远离均匀分布,是我们需要的。
,它的注意力概率 p 更“波动”,也就是更加远离均匀分布,是我们需要的。
3.3 ProbSparse稀疏自注意力机制
核心思想:不能为每个quey都计算下稀疏性得分吧?这样不但没有优化效率,还带来
了额外的计算量。作者利用点积结果服从长尾分布的假设,提出在计算每个quey稀疏
性得分时,只需要和采样出的部分key计算就可以了。就是找到这些重要的/稀疏的query,从而只计算这些queryl的attention值,来优化计算效率。
允许每个键只关注前![]() 个主要查询:
个主要查询:
![]()
其中![]() 是与
是与![]() 相同大小的稀疏矩阵,它只包含在稀疏度量
相同大小的稀疏矩阵,它只包含在稀疏度量![]() 下的前
下的前 ![]() 个查询。受常数采样因子
个查询。受常数采样因子![]() 控制,我们设置
控制,我们设置![]() ,这使ProbSparse自注意力仅需要为每个查询-键查找计算
,这使ProbSparse自注意力仅需要为每个查询-键查找计算![]() 个点积,并且内存使用量是
个点积,并且内存使用量是![]() 。此注意力为每个头生成不同的稀疏查询-键对,从而避免了严重的信息损失。
。此注意力为每个头生成不同的稀疏查询-键对,从而避免了严重的信息损失。
然而,对所有查询点计算![]() ,时间复杂度是
,时间复杂度是![]() ,受此启发,提出了最大均值测量
,受此启发,提出了最大均值测量
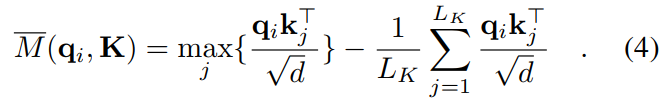
前 ![]() 个的范围近似保持在边界放松中。 在长尾分布下,我们只需要随机采样
个的范围近似保持在边界放松中。 在长尾分布下,我们只需要随机采样![]() 个点积对来计算
个点积对来计算![]() ,即填充其他对为零。然后,我们从中选择稀疏的前
,即填充其他对为零。然后,我们从中选择稀疏的前 ![]() 个作为
个作为![]() 。
。![]() 中的最大运算符对零值不太敏感,且数值稳定。在实践中,查询和键的输入长度通常在自注意力计算中是相等的,即
中的最大运算符对零值不太敏感,且数值稳定。在实践中,查询和键的输入长度通常在自注意力计算中是相等的,即![]() ,因此ProbSparse自注意力的总时间复杂度和空间复杂度为
,因此ProbSparse自注意力的总时间复杂度和空间复杂度为![]() 。
。
- 公式(4)比公式(3)更加利于计算
的作用是计算点
的波动性,数值越大,证明波动性越大。
3.4 Encoder编码器
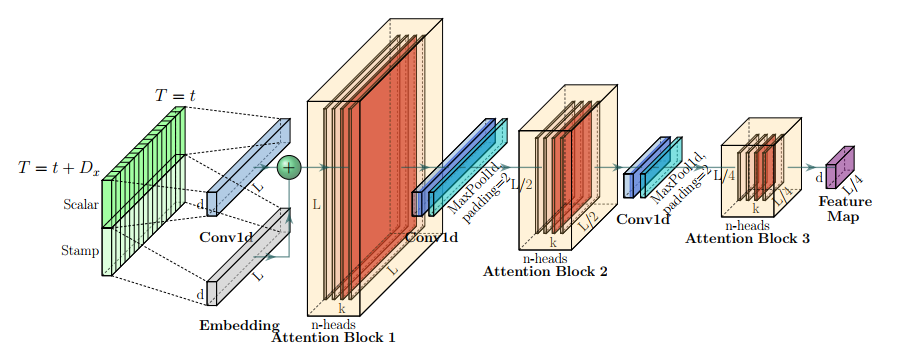
Encoder在内存使用限制下允许处理更长的顺序输入,编码器旨在提取长顺序输入的稳健长程依赖性。在输入表示之后,第 t 个序列输入![]() 已被塑造成一个矩阵
已被塑造成一个矩阵![]() 。
。
自注意力精炼:作为ProbSparse自注意力机制的自然结果,编码器的特征图具有冗余的值![]() 组合。我们使用精炼操作来优先考虑具有主导特征的优越组合,并在下一层中形成一个聚焦的自注意力特征图。它锐利地修剪输入的时间维度,观察图3中注意力块的n头权重矩阵(重叠的红色方块)。受到扩张卷积的启发,我们的“精炼”过程从第 j 层向(j + 1)层前进,如下所示:
组合。我们使用精炼操作来优先考虑具有主导特征的优越组合,并在下一层中形成一个聚焦的自注意力特征图。它锐利地修剪输入的时间维度,观察图3中注意力块的n头权重矩阵(重叠的红色方块)。受到扩张卷积的启发,我们的“精炼”过程从第 j 层向(j + 1)层前进,如下所示:
![]()
这里的 ![]() 代表注意力块。它包含了多头ProbSparse自注意力和基本操作,其中
代表注意力块。它包含了多头ProbSparse自注意力和基本操作,其中![]() 对时间维度进行1-D卷积滤波(核宽度为3),并使用
对时间维度进行1-D卷积滤波(核宽度为3),并使用![]() 激活函数。我们添加了一个步长为2的最大池化层,并在堆叠一层之后将
激活函数。我们添加了一个步长为2的最大池化层,并在堆叠一层之后将![]() 降采样为其一半的片段,从而将整个内存使用减少为
降采样为其一半的片段,从而将整个内存使用减少为![]() ,其中
,其中![]() 是一个小数。为增强精炼操作的稳健性,我们建立了主堆栈的副本,并逐渐减少自注意力精炼层的数量,每次丢弃一层,就像图2中的金字塔一样,以使它们的输出维度对齐。因此,我们连接所有堆栈的输出,并得到编码器的最终隐藏表示。
是一个小数。为增强精炼操作的稳健性,我们建立了主堆栈的副本,并逐渐减少自注意力精炼层的数量,每次丢弃一层,就像图2中的金字塔一样,以使它们的输出维度对齐。因此,我们连接所有堆栈的输出,并得到编码器的最终隐藏表示。
3.5 Decoder解码器
提出了生成式的decoder机制,在预测序列(也包括inferencel阶段)时一步得到结果,而不是step-by-step,直接将预测时间复杂度降低。
Transformer是一个encoder-decoder的结构,在训练阶段,我们可以用teacher forcing的手段
让decoder-一步就得到预测结果,但是inferencel时,都是step-by-step,所以看到Informer中的“一步Decoder”,作者的做法也很简单直接,首先,不论训练还是预测,Decoder的输入序列分为两部分。Informer使用的Decoder和传统的Decoder不同,生成式decoder一次性生成所有的预测输出,而传统的Transformer是将上一步的输出放入decoder在得到下一步的输出,这样每步只能输出一个time step的数据。这种形式的decoder的start token是从input中sample一个较短的序列(需要预测的序列的之前一个片断),decoder输入是encoder输入的后面部分的截取+与预测目标形状相同的0矩阵。
解码器生成长序列输出,通过一次前向过程我们在图(2)中使用了标准的解码器结构,它由两个相同的多头注意力层堆叠而成。然而,在长序列预测中,采用生成式推断来缓解速度下降。我们将以下向量作为解码器的输入:
![]()
这里![]() 是起始标记,
是起始标记,![]()
![]() 是目标序列的占位符(标量设为0)。在ProbSparse自注意力计算中应用了掩码多头注意力,通过将掩码点积设为
是目标序列的占位符(标量设为0)。在ProbSparse自注意力计算中应用了掩码多头注意力,通过将掩码点积设为![]() ,防止每个位置关注到后续位置,避免自回归。最终输出由全连接层获取,其输出大小
,防止每个位置关注到后续位置,避免自回归。最终输出由全连接层获取,其输出大小![]() 取决于我们是执行单变量预测还是多变量预测。
取决于我们是执行单变量预测还是多变量预测。
生成式推断:起始标记在NLP的“动态解码”中得到了高效应用,我们将其扩展为一种生成式方式。我们不是选择特定的标记作为令牌,而是在输入序列中随机抽样一个长度为![]() 的序列,比如在输出序列之前的一个较早的片段。以预测168个点为例(实验部分的7天温度预测),我们将取目标序列之前已知的5天作为“起始标记”,并将其与
的序列,比如在输出序列之前的一个较早的片段。以预测168个点为例(实验部分的7天温度预测),我们将取目标序列之前已知的5天作为“起始标记”,并将其与![]() 一起作为生成式推断解码器的输入,即
一起作为生成式推断解码器的输入,即![]() 。这里的
。这里的![]() 包含目标序列的时间戳,即目标周的上下文。然后我们的提出的解码器通过一次前向过程而不是在传统的编码器-解码器架构中耗时的“动态解码”来预测输出。在计算效率部分给出了详细的性能比较。
包含目标序列的时间戳,即目标周的上下文。然后我们的提出的解码器通过一次前向过程而不是在传统的编码器-解码器架构中耗时的“动态解码”来预测输出。在计算效率部分给出了详细的性能比较。
这篇关于时间序列预测(8) — Informer模型原理的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!


