Bellman_Ford 算法 | POJ 3259 虫洞（Bellman-Ford算法

本文主要是介绍Bellman_Ford 算法 | POJ 3259 虫洞（Bellman-Ford算法 · 板子题），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

需求

对于解决单源最短路的问题，Dijkstra 是一个很好的方法，但是解决不了对于含有负权图的问题，所以 Bellman_Ford 算法就可以完美的解决这个问题。

个人思考

学完 Dijkstra 算法后，再学习Bellman_Ford算法的时候，是有点懵的，因为对于这个过程了解的不是很清楚，再加上学完之后做的题目的问题更是让我栓Q了，今天总算是基本明白了。

核心代码

对于一条边a -> b，边权为w
for(k = 1; k <= n - 1; k++)for(i = 1; i <= m; i++)dist[b] = min(dist[b], dist[a] + w);

源码分析

1.外循环：顶点有 n 个，循环n - 1次。
2.内循环：m 表示边的个数，循环 m次。
dist[b] = min(dist[b], dist[a] + w);
这一行的意思是能不能通过a -> b这条边，使得1 -> b 的距离变短

问题

为什么要进行n - 1次循环呢
因为在一个含有 n 个顶点的图中，任意两个顶点之间的最短路径最多包含 n - 1边

最短路径中不可能包含回路吗？
答案是：不可能！！！如果最短路径中包含正权回路，那么去掉这个回路，一定可以得到更短的路径。
如果最短路径中包含负权回路那么肯定没有最短路径，因为每多走一次负权回路就可以得到更短的路径 . .

问题

Wormholes

题目分析

Description

当走访自己的农场时，农夫 John（下称 FJ）发现了许多神奇的虫洞。虫洞是一个很奇怪的东西，因为它是一个能够将你送到一个时间位于你进入虫洞之前的目的地的单向路径。FJ 的每个农场包含 N 块田（1 ≤ N ≤ 500），编号从 1 到 N ，M 条路（1 ≤ M ≤ 2500），W 个虫洞（1 ≤ W ≤ 200）。
FJ 是一个狂热的时间旅行爱好者，他希望做这样的事：从某块田开始，经过一些路径和虫洞，最后回到起始位置且到达时的时间在他出发之前。他有可能与他自己碰面 ? 。
为了帮助 FJ 求出这是否可能成功，他会告诉你他的农场的 F 个地图（1 ≤ F ≤ 5）。没有路径花费超过 10 000 秒才能走完，也没有虫洞能够将 FJ 带回早于进入虫洞的时刻的 10 000 秒之前。

Input

第一行：一个整数 F ，描述如上。
接下来对每个农场，第一行三个整数，空格分隔：N、M、W。
接下来 M 行，每行三个整数，空格分隔：S、E、T，分别描述：存在点 S 到点 E 的双向路径，单程花费 T 秒。两块田之前可以被超过一条路连接。
接下来 W 行，每行三个整数，空格分隔：S、E、T，分别描述：存在点 S 到点 E 的单向路径，能够令进入者回到 T 秒之前。

Output

1 到 F 行：对每个农场，如果 FJ 可以达成他的目标，输出

YES

否则输出

NO

Sample Input

Sample Output

NO
YES

Hint

对农场 1，FJ 并不能穿越到出发之前。
对农场 2，FJ 可以沿闭环 1→2→3→1 行进，在他出发之前回到出发地 1。他可以从这个环路上的任意位置出发来完成目标。

思路

先拿第二个样例来讲
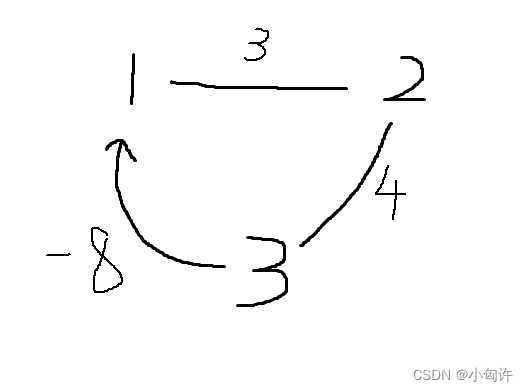
在这里插入图片描述

假设当前时间为0，那么从1 -> 2 所花费的时间为 3s ，再从2 -> 3所花费的时间为 4s，然后再从虫洞从3 -> 1，时光倒流，回到 8s 之前到达 1，就可以在出发之间和自己碰面。

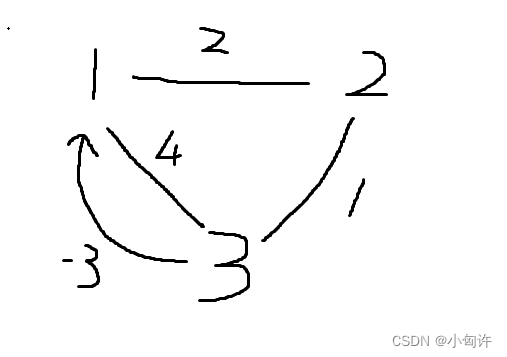
在这里插入图片描述

和样例2的步骤一样，当我们从 1 经过 2 ，3 再回到 1的时候，时间刚好是0s 初始的时候，这个时候自己是刚出发，所以自己是不能和自己碰面的

所以这个题目就可以判断，是否有一个负权边，能够在出发之前和自己碰面。

第一个问题，是否存在负权边
第二个问题，存在的负权边是否能符合题意

解决方法，在 n 遍循环的时候，如果dist数组里的内容没有变化，说明不存在或者是存在的负权边不能够满足题意，就像第2个图片，如果满足题意，那么在更新第 n 次循环的时候，dist数组里就会有变化，就拿一个图片为例
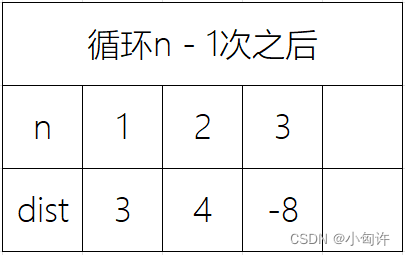
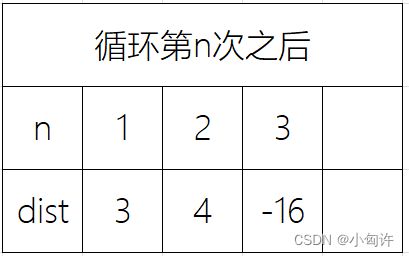
在这里插入图片描述

代码

#include <cstring>
#include <iostream>
#include <algorithm>using namespace std;const int N = 6010;int n, m, w, k;
int dist[N];
int last[N];struct Edge
{int a, b, w;
}edges[N];bool Bellman_Ford()
{memset(dist, 0x3f, sizeof(dist));dist[1] = 0;for(int i = 1; i < n; i ++){memcpy(last, dist, sizeof(last));// 优化：如果当前已经完成了最短路的构建，那么就可以不用把循环执行完，就可以直接跳出，方法就是上一次的状态和当前状态是否相同for(int j = 1; j <= k; j ++){int a = edges[j].a, b = edges[j].b, w = edges[j].w;dist[b] = min(dist[b], dist[a] + w);}bool flag = false;for(int j = 1; j <= n; j ++){// 判断是否已经完成了构建if(dist[j] != last[j]){flag = true;break;}}if(!flag) break;}for(int j = 1; j <= k; j ++){int a = edges[j].a, b = edges[j].b, w = edges[j].w;if(dist[b] > dist[a] + w){return false;}}return true;
}int main()
{int t;cin >> t;while(t -- ){k = 0;cin >> n >> m >> w;for(int i = 1; i <= m; i ++){int a, b, w;cin >> a >> b >> w;edges[++ k] = {a, b, w};edges[++ k] = {b, a, w};}for(int i = 1; i <= w; i ++){int a, b, w;cin >> a >> b >> w;edges[++ k] = {a, b, w * (-1)};}bool t = Bellman_Ford();if(!t) puts("YES");else puts("NO");}return 0;
}