眼图的判断 蒙特卡洛标准差

在无码间串扰和噪声的理想情况下，波形无失真，“眼”开启得最大。当有码间串扰时，波形失真，引起“眼”部分闭合。若再加上噪声的影响，则使眼图的线条变得模糊，“眼”开启得小了，因此，“眼”张开的大小表示了失真的程度。由此可知，眼图能直观地表明码间串扰和噪声的影响，可评价一个基带传输系统性能的优劣。另外也可以用此图形对接收滤波器的特性加以调整，以减小码间串扰和改善系统的传输性能。通常眼图可以用图7.6所示的图形来描述。

1）眼图张开的宽度决定了接收波形可以不受串扰影响而抽样再生的时间间隔。显然，最佳抽样时刻应选在眼睛张开最大的时刻。

2）眼图斜边的斜率，表示系统对定时抖动（或误差）的灵敏度，斜边越陡，系统对定时抖动越敏感。

3）眼图左（右）角阴影部分的水平宽度表示信号零点的变化范围，称为零点失真量，在许多接收设备中，定时信息是由信号零点位置来提取的，对于这种设备零点失真量很重要。

4）在抽样时刻，阴影区的垂直宽度表示最大信号失真量。

5）在抽样时刻上、下两阴影区间隔的一半是最小噪声容限，噪声瞬时值超过它就有可能发生错误判决；

6）横轴对应判决门限电平

眼图的垂直张开度反映信码幅度的变化量，可用来表示系统的抗噪声能力，垂直张开度越大，抗噪声能力越强。水平张开度则反映信码的码间干扰。水平张开度越大，表示信码的码间干拢越小。垂直张开度与水平张开度越大，越有利于信码再生器的判决，还原出来信码的误码率就越小。

标准差（Standard Deviation） ，是离均差平方的算术平均数（即：方差）的算术平方根，用σ表示。标准差也被称为标准偏差，或者实验标准差，在概率统计中最常使用作为统计分布程度上的测量依据。

标准差是样本数据到平均数的一种平均距离，一般用s表示.

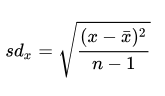
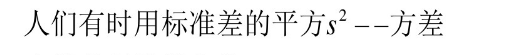
标准差的取值范围：[0，+00）

标准差为0的样本数据都等于样本平均数.

标准差表现为：标准差越大，表明数据的离散程度就越大；反之，标准差越小，表明各数据的离散程度就越小。