【数据结构与算法暑期实习】PTA 三足鼎立

一、题目

当三个国家中的任何两国实力之和都大于第三国的时候，这三个国家互相结盟就呈“三足鼎立”之势，这种状态是最稳定的。现已知本国的实力值，又给出 n 个其他国家的实力值。我们需要从这 n 个国家中找 2 个结盟，以成三足鼎立。有多少种选择呢？

输入格式：
输入首先在第一行给出 2 个正整数 n（2≤n≤1e5）和 P（≤1e9），分别为其他国家的个数、以及本国的实力值。随后一行给出 n 个正整数，表示n 个其他国家的实力值。每个数值不超过 10^​9，数字间以空格分隔。

输出格式：
在一行中输出本国结盟选择的个数。

输入样例：
7 30
42 16 2 51 92 27 35

输出样例：
9

样例解释：
能联合的另外 2 个国家的 9 种选择分别为：
{16, 27}, {16, 35}, {16, 42}, {27, 35}, {27, 42}, {27, 51}, {35, 42}, {35, 51}, {42, 51}。

二、思路

由题意，“三足鼎立”的条件相当于三角形三边关系：a+b>c，a+c>b，b+c>c。其中一条边为已知。三个约束条件，两个变量，考虑变换形式，使其中一个变量可以表示另一个。将约束条件整理为：|a-b|<c<a+b，b为已知，可以b为自变量推出的c的变化范围，于是题意变为：求在给定的b下，满足条件的c有多少个，进而可以用二分搜索求出上下界从而求解。

另外需要注意的是，使用二分搜索时序列必须为有序序列。因此首先要对输入的国家序列进行排序。这里使用的是堆排序。（本次实习中不可以用stl，需要自己写sort。简单选择排序和快速排序都不行，会超时）

关于排序算法：

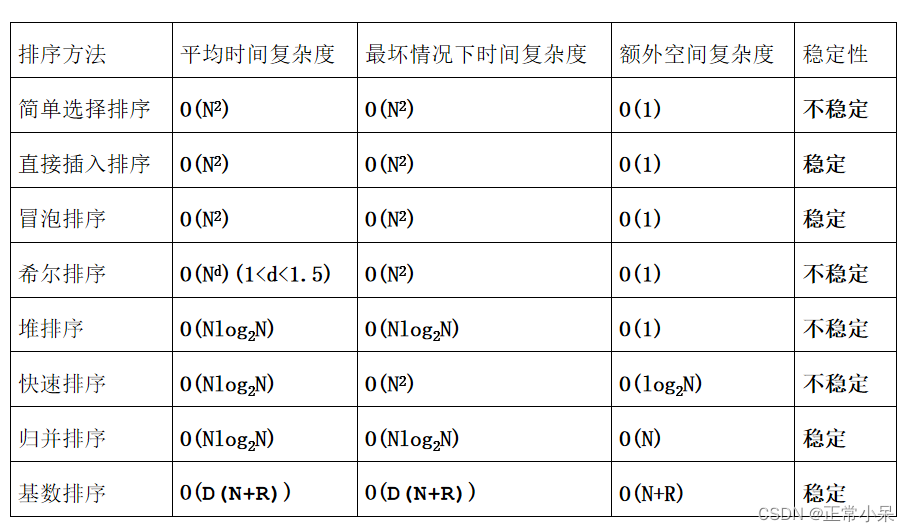
快速排序在n很大时效果不好，但是堆排序就很适合用于n较大的情况。

三、代码

堆排序

#include<stdio.h>
#include<stdlib.h>
#include<time.h>/* 堆排序中的一次调整 */
void OneAdjust(long long* arr, long long len, long long root)
{int tmp = arr[root];int left = 2 * root + 1;int right = 2 * root + 2;while (left < len){int max = left;/*找左右孩子中谁的值更大*/if (right < len && arr[left] < arr[right]){max = right;}/*若左右孩子中的较大者，也小于当前子树的根结点，则不变；否则令该根结点的数值与左右孩子中的较大者交换*/if (arr[max] < tmp){break;}else {arr[root] = arr[max];root = max;left = 2 * root + 1;right = 2 * root + 2;}}arr[root] = tmp;
}/* 建立大根堆 */
void CreateHeap(long long* arr, long long len)
{int root = (len-2)/2;//最后一个结点的下标是len-1，算出的root为最后一棵子树的根结点下标，也就是从此处开始调整堆。for (; root >= 0; --root){OneAdjust(arr, len, root);}
}/* 交换函数 */
void Swap(long long* x, long long* y)
{long long tmp = *x;*x = *y;*y = tmp;
}/* 堆排序 */
void HeapSort(long long* arr, long long len)
{CreateHeap(arr, len);for (int i = 0; i < len - 1; ++i){Swap(&arr[0], &arr[len-1-i]);OneAdjust(arr, len-i-1,0); //(len-i-1)表示当前步所调整的树的最大下标。}
}

主程序（二分搜索）

int main()
{long long n, mypower;long long othersPower[100001];long long num = 0;scanf_s("%lld %lld", &n, &mypower);//注意输出的特殊格式for (long long i = 0; i < n; i++) {scanf_s("%lld", &othersPower[i]);}HeapSort(othersPower, n);for (long long i = 0; i < n; i++){long long min = abs(mypower - othersPower[i]); //下界abs(a-b)long long max = mypower + othersPower[i]; //上界a+b.程序要求的就是处于上下界之间的元素个数。long long left = i + 1, right = n - 1; long long num1, num2 = 0;//二分查找，在升序序列中找到符合要求的起始点。while (left <= right){long long mid = (left + right + 1) / 2;if (othersPower[mid] > min)  right = mid - 1;else left = mid + 1;}num1 = left;left = i + 1, right = n - 1;//二分查找，在升序序列中找到符合要求的起始点。while (left <= right){long long mid = (left + right + 1) / 2;if (othersPower[mid] >= max) right = mid - 1;else left = mid + 1;}num2 = right;num =num + num2 - num1 + 1;}printf("%lld", num);return 0;
}