空间统计学：快速理解反距离加权法（IDW）

空间插值

说到反距离加权法，首先我们要先了解空间插值的概念

对于一个平面，我们并不能获取所有区域的精确信息，所以一般情况下，我们通过采样的方式只获取部分点的信息。然后通过空间插值，计算出一个区域所有的数据

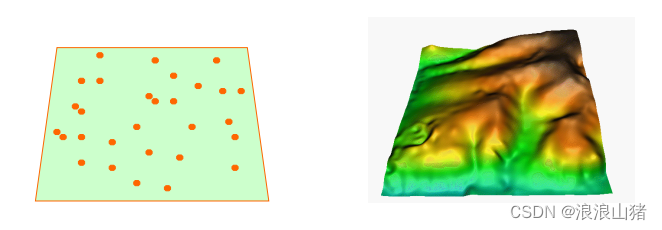
左图我采样了部分点的高程数据，右图我通过这部分高程数据，通过空间插值计算出所有区域的数据。

具体插值原理是什么呢，见下图

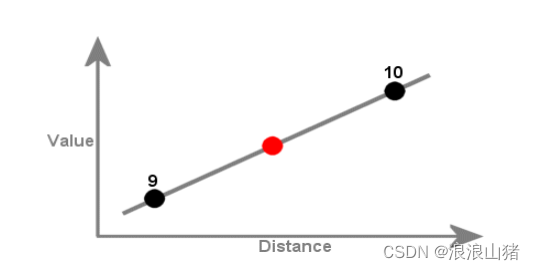
 9和10是数据已知的点，那么我通过两点的数据，结合它们之间的距离，我就可以估算出红点的具体数据。

对于空间上的点来说，未知值的点与样本点之间的距离决定了其最终值的估计。

那么具体他是怎么结合距离数据和本身的值计算位置数据的呢？常用的插值方法包括反距离加权法（IDW）、克里金（Kriging）等。那么本篇文章就是讲解其中之一的反距离加权法。

反距离加权法（IDW)

反距离加权法（Inverse Distance Weighting, IDW）是一种常见的空间插值方法，常用于将已知分散的样点数据插值为连续的地表或地下场景。下面是反距离加权法的简要步骤：

1. 确定待插值位置和已知样点位置。
2. 根据待插值位置与已知样点的欧几里得距离（或其他距离指标），计算每个样点的权重，一般权重与距离的倒数成正比。
3. 使用每个样点的权重对其函数值进行加权平均，得到插值结果。

下面详细解释这三个步骤：

1. 确定待插值位置和已知样点位置

首先我们需要确定待插值位置的坐标和范围，以及已知样点的坐标和数值。

2. 计算权重

对于每个待插值位置，我们需要计算它与所有已知样点的距离，并将距离转化为权重。一般来说，样点与待插值位置之间的欧几里得距离越小，样点对插值结果的影响就越大，因此权重与距离成反比，可使用以下公式计算：

其中 wi​ 是第 i 个样点的权重，di​ 是该样点与待插值位置的距离，p 是一个可调参数，一般取值为 2 （欧几里得距离）或 3 （曼哈顿距离），也可以通过交叉验证等方法来确定最优的 p 值。 

3. 加权平均求解

计算出每个已知样点的权重后，我们可以将它们的函数值进行加权平均，得到待插值位置的函数值。具体地，设已知样点的个数为 N，第 i 个样点的坐标为 (xi​,yi​)，权重为 wi​，函数值为 zi​，则待插值位置的函数值z(x,y) 可以通过以下公式计算：

 其中分子为各样点函数值乘以对应权重的总和，分母为权重之和，它们的比值即为插值结果。

反距离加权法的优缺点

反距离加权法的主要优点是简单易用，而且在样点分布相对均匀的情况下效果较好。它也有一些缺点，例如插值结果表现出的锯齿状特征、函数值抖动等问题。为解决这些问题，通常需要采用其他空间插值方法，例如径向基函数插值（Radial Basis Function, RBF）、克里金插值等。

代码实现

使用 Python 的 Matplotlib 库生成反距离加权法（IDW）插值示意图

import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import Rbf# 构造样点数据
np.random.seed(0)
x = np.random.rand(20) * 10 - 5
y = np.random.rand(20) * 10 - 5
z = np.sin(np.sqrt(x**2 + y**2))
xi, yi = np.meshgrid(np.linspace(-5, 5, 50), np.linspace(-5, 5, 50))# 计算插值结果
rbf = Rbf(x, y, z, function='inverse')
zi = rbf(xi, yi)# 绘制示意图
plt.imshow(zi, cmap='rainbow', extent=(-5, 5, -5, 5))
plt.colorbar()
plt.scatter(x, y, c=z, cmap='rainbow', edgecolors='black', linewidths=1)
plt.title('Inverse Distance Weighting Interpolation')
plt.xlabel('X')
plt.ylabel('Y')
plt.show()

 解释代码：

第一部分：

当我们使用反距离加权法对二维数据进行插值时，需要确定已知样点的位置和对应数值，以及待插值位置的坐标。内容包括通过numpy库生成20个随机的二维坐标点，并在这些点上计算对应的函数值。在x轴和y轴上各取50个均匀分布的点，形成二维网格，作为插值结果的横纵坐标。

第二部分：

利用scipy库中的Rbf函数进行插值，并指定插值函数为inverse distance weighting（IDW)。

第三部分：

将插值结果用彩虹色表现出来，并添加颜色条、散点图等元素，以便更好地展示

结果

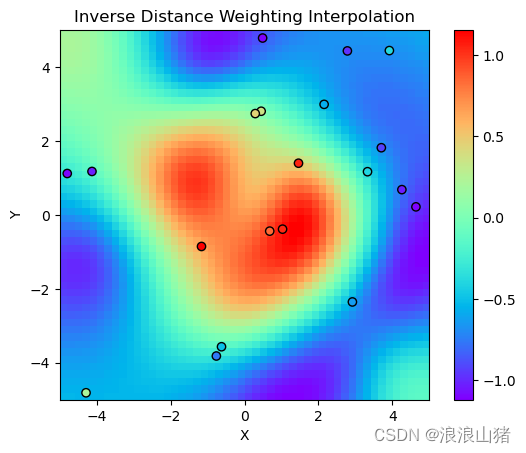
其中：

• 圆点表示已知样点，每个样点都有一个数值。
• 彩色网格表示未知区域，我们需要计算这些位置的数值。
• 网格上的每个颜色块表示对应位置的插值结果，颜色越深表示对应位置的数值越大。

通过反距离加权法，可以计算未知区域内每个网格点的数值。以左上角网格点为例，其数值可通过对已知样点进行加权平均得到，权重与样点间的距离成反比，距离越近的样点权重越大。最终得到的插值结果可用于制图、分析等用途。

在该图中，我们可以观察到：

• 插值结果整体呈现出类似于圆形的形状，与样点分布的形状有关。
• 在样点位置附近，插值结果的颜色更深，数值更大；而在远离样点的位置，插值结果的颜色较浅，数值较小。
• 样点之间的插值结果呈现出类似于“锯齿状”的形态，在实际应用过程中需要注意。

总的来说，反距离加权法是一种简单而有效的空间插值方法，适用于各种数据类型和应用领域。