论文导读 | 对于LSM Tree的一系列优化工作

研究背景

LSM Tree是Log-Structured Merge Tree的缩写。作为一种多层级的数据结构，LSM相Tree对于其他有序的数据结构，比如有序列表，LSM Tree具有更新快，访存效率高等特点。如今被应用在很多需要大量存储访问和更新的场景中。

LSM Tree由L层的有序数组构成。随着层数增多，每一层有序数组（Run）的大小也会成倍扩展。LSM Tree分为Leveled和Tiered两种构造。Leveled结构中，每一层只有一个Run；而在Tiered结构中，每一层存在T个Run。

Leveled与Tiered的更新方式也不同。如图所示，当Leveled的一层数据存满后，这一层数据会向下和下一层数据合并。而Tiered的一层数据存满后，这一层数据会进行合并，然后和下一层数据平行储存。因此Leveled结构的查询复杂度低，而更新复杂度高；而Tiered的更新复杂度低，而查询复杂度相对较高。

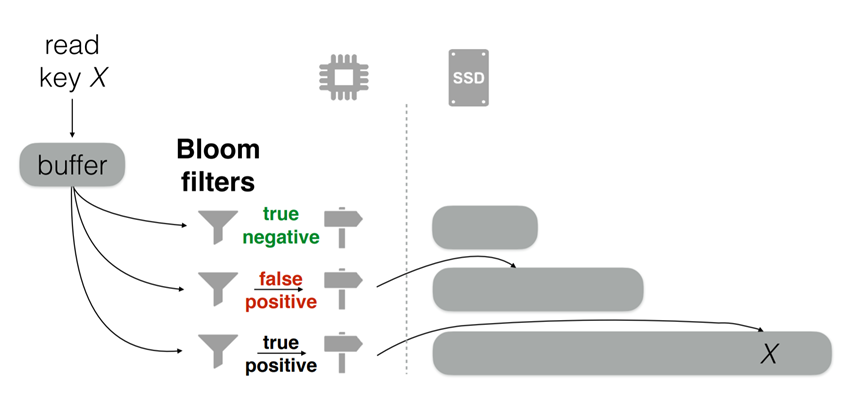
LSM Tree通常会把主要数据结构储存在Secondary Storage当中，比如SSD硬盘。而在内存里，会保留每一层储存数据的索引信息，从而提高访存效率。如图中所示，所有的Run会被分成页，然后在内存中储存这些页的上线界和指针（FP）。这样一次访存就可以从SSD中获得需要的数据。同时对于每一个Run，LSM Tree都会建立一个Bloom Filter（BF）。通过BF可以判断查询的元素是否存在于LSM Tree中。使用BF可以减少访存次数。

SIGMOD 2017. Best of SIGMOD 2017

这篇论文提出了在以往的LMS Tree中，每个Run的BF大小和数组大小的比例相同，这样保证了每个BF都拥有相同的假阳性率。如果一个元素不在LSM Tree当中，每一次BF的假阳性，我们就需要访问一次SSD。查询获得空结果的访存代价，由每个BF的假阳性率相加决定。

由于FP的存在，无论Run的大小有多大，我们都只需要进行一次访存。但是由于LMS Tree随着层数增长，每一层的大小在成倍扩大。如果要维持相同的假阳性率，BF的大小也要成倍扩大。如果给定内存空间，那么降低下层假阳性率，要比降低上层假阳性率，更有效率。

因此在Monkey这个数据结构中，不再维持每一层BF相同的假阳性率，而是成倍降低假阳性率，在最高几层可以取消BF。如图所示：

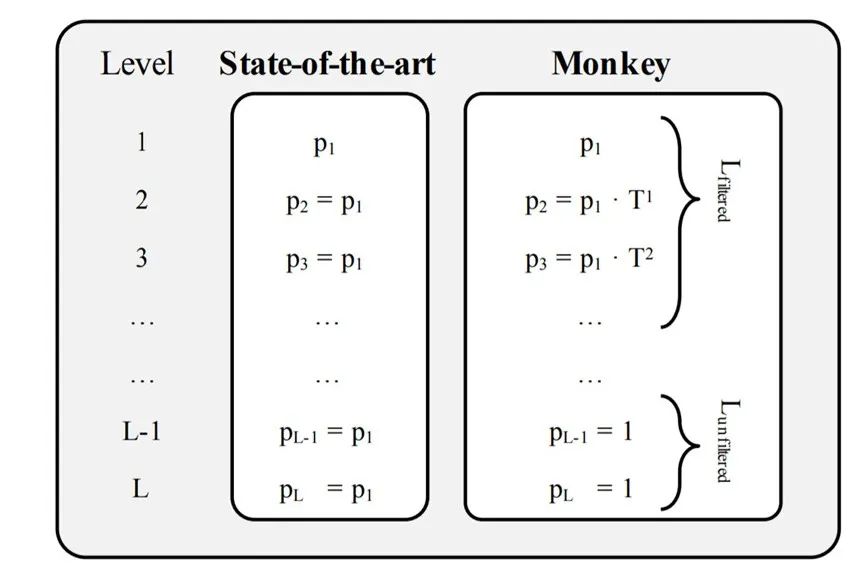
利用Monkey的设计，在有限的内存空间里，可以更高效地利用BF的筛选作用，大大降低访存次数，提高数据结构的查询性能。

SIGMOD 2018

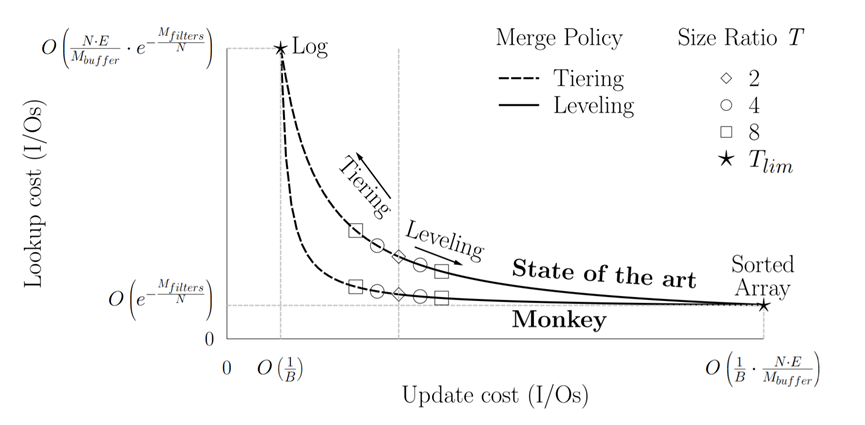
对于LSM Tree，Leveled结构的查询复杂度低，而更新复杂度高；而Tiered的更新复杂度低，而查询复杂度相对较高。这篇论文，为了平衡两种结构的优缺点，提出了Lazy Leveling的合并策略。

Lazy Leveling在前n-1层，都使用Tiering的合并策略，尽在最后的第n层，使用leveling的策略。如图所示，使用了Lazy Leveling策略后，与Leveling相比，在点查询，大范围查询两项，Lazy Leveling都拥有相同的复杂度。在小范围查询Leveling复杂度更低，而在合并操作中，Lazy Leveling更有优势。与Tiering相比，除了合并操作，另外三个查询操作Lazy Leveling都有更低的复杂度。因此Lazy Leveling可以实现更平衡的性能。

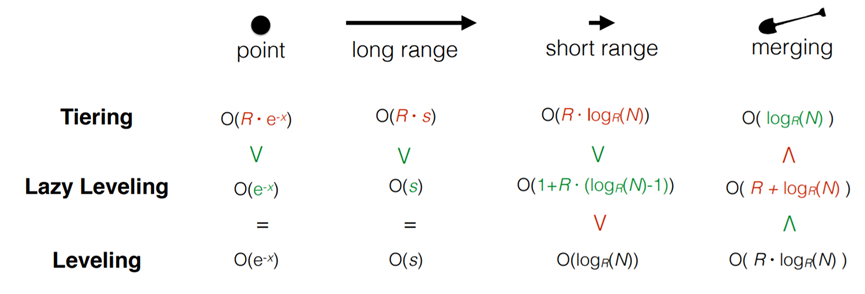
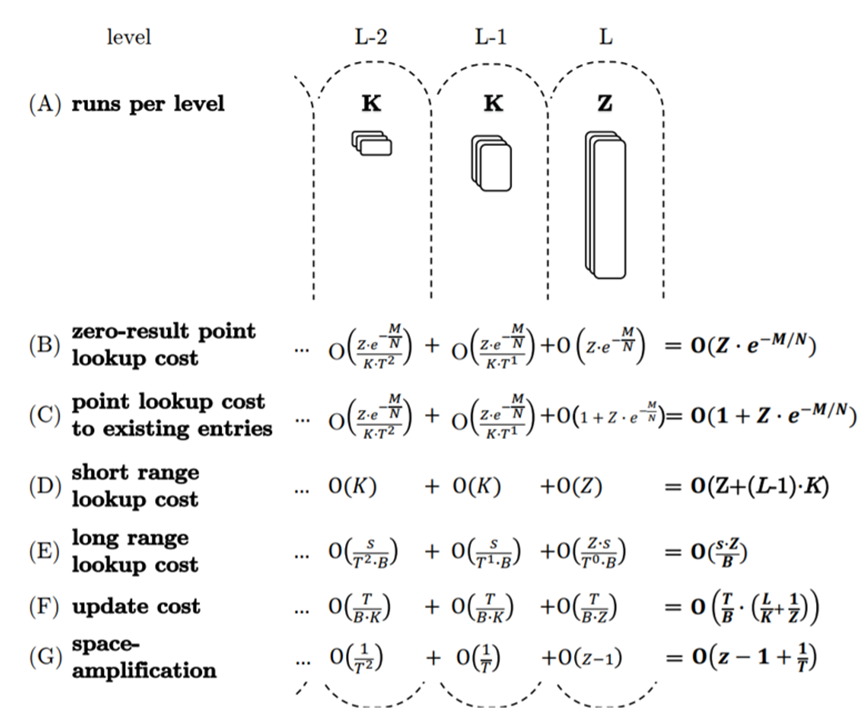
在Lazy Leveling的基础上，本篇论文又提出了流动的LSM Tree构造。如图所示，流动的LSM Tree中，定义了两个参数K和Z。K是非最后一层中每一层的有序列表数，而Z则是最后一层的有序列表数。如果K=Z=1，则为Leveled结构；如果K=Z>1，则为Tiered结构；如果K>1且Z=1，则为Lazy Leveling结构。用户可以根据工作负载的不同，来选取最合适的参数值，从而获得最好的性能。

SIGMOD 2021

随着SSD性能的提升，对于硬盘内数据的访问渐渐不再是LSM Tree的唯一瓶颈。在现实当中，比较庞大的LSM Tree可能拥有数十上百层，每一层最多可能拥有数百个Run。当我们在进行查询时，对每一个Run都要进行BF的查询。数千BF的查询正在成为新的性能瓶颈。下图为不同策略下，I/O的复杂度：

因此在本篇论文中，作者提出了使用Cuckoo Filter（CF）来取代BF的策略Chucky。Chucky使用一个CF来取代所有的BF。在CF的每一个位置上，会储存一个hash指纹，和这个元素在LSM Tree中的位置。当我们查询的时候，只需要查询CF一次，即可获得元素的储存位置，而不再需要查询大量的BF。

通过使用CF，可以把LSM Tree的I/O的复杂度降低为：

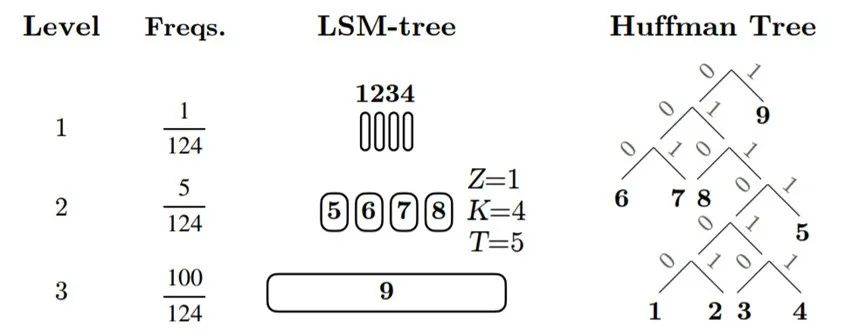
在CF中，每一个位置都要存储元素所在Run的位置。为了降低CF的内存开销，文章提出了一个压缩思路：下层的每个Run的空间更大，因此储存的数据也最多。因此在CF中下层的指针出现次数也最多。如果我们对所有的指针编码，下层的编码较短，上层编码较长，那么就能更好地利用空间。

本文采用了霍夫曼编码，对于每一个Run的指针，按照出现的概率，也就是Run的大小占总空间的比例，来进行编码。从而实现了上层Run编码长，下层Run编码短的编码结果。

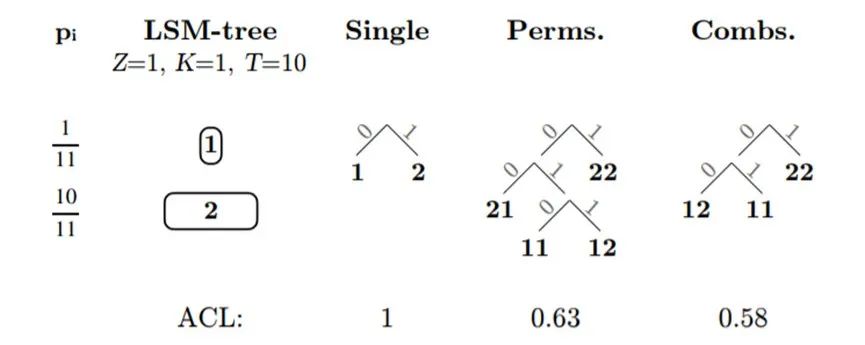
为了进一步压缩空间，本文还使用了组合的方式，将相邻两个元素组合在一起进行编码：

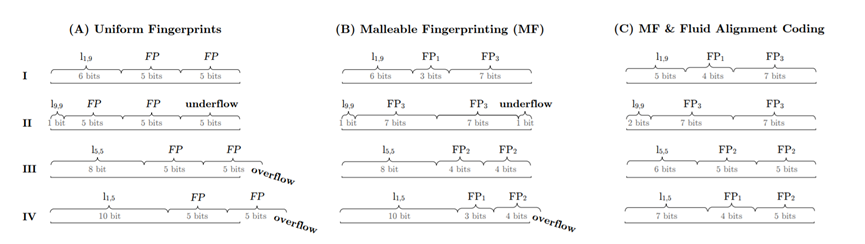
但这种编码带来了新的问题，由于每个元素所在的Run指针编码不同，导致无法对其。本文采用了可变动的指纹策略。由于下层Run指针编码短，因此下层储存的元素hash指纹较长，通过可变的hash指纹长度，实现了CF的对齐。