解决Poi-tl动态生成表格（行列都不确定的情况）

1、新增策略DetailTablePolicy，继承于抽象表格策略DynamicTableRenderPolicy

/*** 自定义动态表格* 重写render方法*/
public class DetailTablePolicy extends DynamicTableRenderPolicy {@Overridepublic void render(XWPFTable table, Object data) throws Exception {if(null == data) return;List<Map<String, Object>> targetRowData = (List<Map<String, Object>>) data;if(ObjectUtil.isNotEmpty(targetRowData) && targetRowData.size()>0){table.removeRow(0);//循环插入行数据for (int i = 0; i < targetRowData.size(); i++) {//第一行是标题行XWPFTableRow xwpfTableRow = table.insertNewTableRow(i);//循环列 row-cellBoolean flag = false;for (Map.Entry vo:targetRowData.get(i).entrySet()) {XWPFTableCell cell = xwpfTableRow.createCell();//单元格赋值cell.setText(vo.getValue().toString());//单元格文字居中CTTc cttc = cell.getCTTc();//文字垂直位置cttc.addNewTcPr().addNewVAlign().setVal(STVerticalJc.CENTER);//非标题行第一列文字居中，其他列文字居右if(i == 0){//文字水平位置cttc.getPList().get(0).addNewPPr().addNewJc().setVal(STJc.CENTER);}else{//文字水平位置if(flag == false){cttc.getPList().get(0).addNewPPr().addNewJc().setVal(STJc.CENTER);}else{cttc.getPList().get(0).addNewPPr().addNewJc().setVal(STJc.RIGHT);}}flag = true;}}}}}

2、调用我们重写的策略，report2.docx是我们的模板，模板里面的表格样式需要我们自定义，poi-tl技术主要针对的是数据处理问题

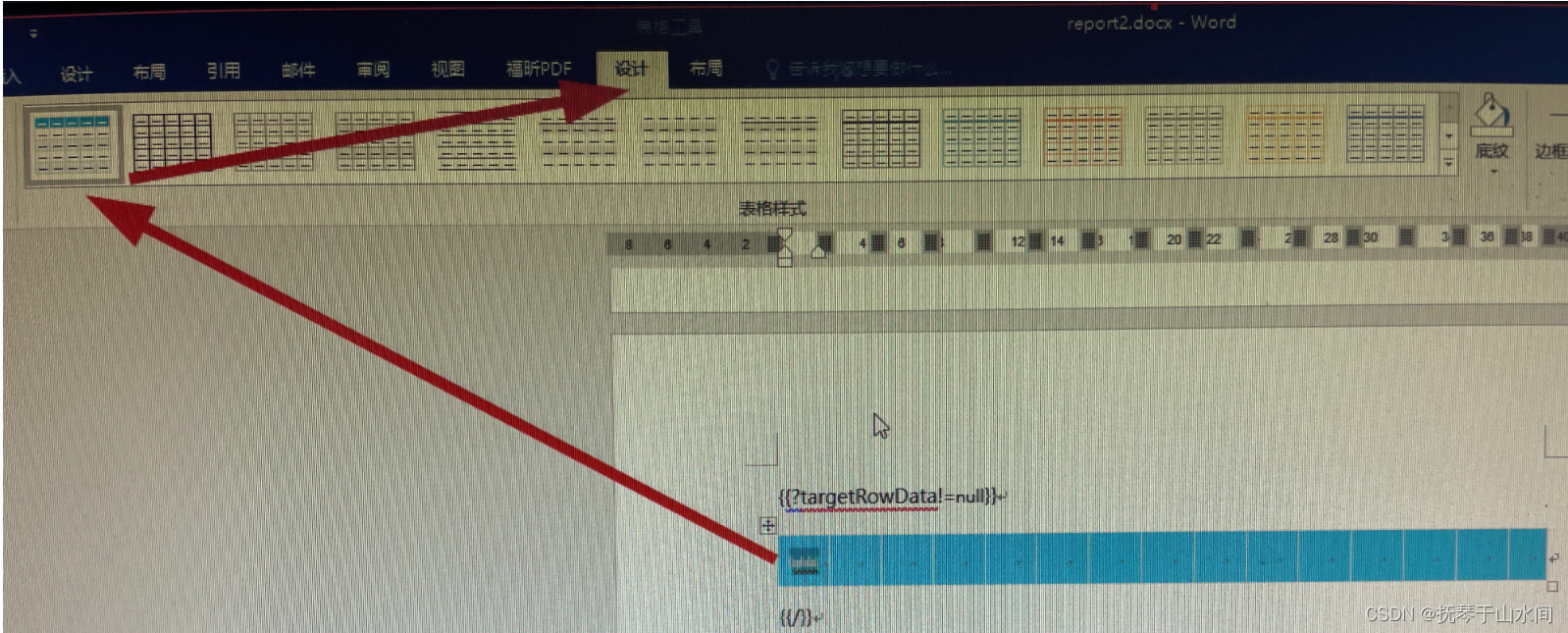
XWPFTemplate template = null;
InputStream templateInputStream = null;
File docFile = null;String fileName = "report2.docx";
templateInputStream = this.getClass().getClassLoader().getResourceAsStream("word/" + fileName);
if (null == templateInputStream) {return JsonBean.returnResponse(false, ResultCode.SERVER_ERROR, "模板文件不存在");
}
ConfigureBuilder builder = Configure.builder();
//配置为SpEL模式
builder.useSpringEL();
//除了标签前后缀外的任意字符
builder.buildGrammerRegex(RegexUtils.createGeneral("{{", "}}"));builder.bind("targetRowData",new DetailTablePolicy());template = XWPFTemplate.compile(templateInputStream, builder.build());
template.render(args);
//输出到文件
String dir ="路径";
String docName = "报告.docx";
docFile = new File(dir, docName);
template.writeToFile(docFile.getAbsolutePath());