MT19937在连续输出存在截断的情况下利用z3符号执行推导内部状态以及等价种子

2023-11-10 16:15
文章标签 输出 存在 状态 连续 情况 内部 种子 推导 截断 z3 符号执行 等价 mt19937

本文主要是介绍MT19937在连续输出存在截断的情况下利用z3符号执行推导内部状态以及等价种子，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

传统针对MT19937的逆向往往需要得到连续且完整的624个随机数，从而逆向出所有内部状态。但在实际场景中，想得到连续且完整的624个随机数是比较困难的，大部分情况下得到的是一些截断的数（例如得到连续的624个数，每个数是原始随机输出中的前16比特）。这种情况下，我们可以利用z3的符号执行推导部分内部状态，甚至可以推导一个“部分等价”的初始种子。本文针对python的random底层c库实现做了详细的分析，并给出了所有中间代码。

关键词：

  • MT19937逆向
  • MT19937基于z3的内部状态求解
  • 复原部分历史随机数生成
  • 从伪随机数的输出构造等价种子

文章目录

  • 1.MT19937及其逆向
    • 1.1 梅森旋转
    • 1.2 MT19937
    • 1.3 MT19937的逆向
    • 4.基于z3的MT19937的内部状态求解
  • 2.连续输出存在截断的情况下z3的求解部分内部状态
    • 2.1 原理
    • 2.2 应用一：完全推导内部状态
    • 2.3 应用二：部分推导，复原部分历史随机数生成
  • 3.生成等价种子
  • 4.完整代码及工具封装
  • 参考

1.MT19937及其逆向

1.1 梅森旋转

先给出维基百科的解释[1]：
在这里插入图片描述
为什么叫梅森旋转？

  • 算法实现的过程中，参数的选取取决于梅森素数。
  • 整个算法的核心操作，是针对状态的旋转。

1.2 MT19937

最为广泛使用Mersenne Twister的一种变体是MT19937，可以产生32位整数序列，其周期非常长，达到 2 19937 − 1 2^{19937}-1 219937−1 。
有关MT19937的所有细节请参考原文：http://www.math.sci.hiroshima-u.ac.jp/m-mat/MT/ARTICLES/mt.pdf

简要实现如下：

def _int32(x):return int(0xFFFFFFFF & x)class MT19937:# 依据seed初始化内部状态（共624个state）def __init__(self, seed):self.mt = [0] * 624self.mt[0] = seedself.mti = 0for i in range(1, 624):self.mt[i] = _int32(1812433253 * (self.mt[i - 1] ^ self.mt[i - 1] >> 30) + i)# 提取一个伪随机数def extract_number(self):if self.mti == 0:self.twist()y = self.mt[self.mti]y = y ^ y >> 11y = y ^ y << 7 & 2636928640y = y ^ y << 15 & 4022730752y = y ^ y >> 18self.mti = (self.mti + 1) % 624return _int32(y)# 旋转状态def twist(self):for i in range(0, 624):y = _int32((self.mt[i] & 0x80000000) + (self.mt[(i + 1) % 624] & 0x7fffffff))self.mt[i] = (y >> 1) ^ self.mt[(i + 397) % 624]if y % 2 != 0:self.mt[i] = self.mt[i] ^ 0x9908b0df

1.3 MT19937的逆向

从上述MT19937的源码中，不难看出，其两个关键的函数都是可逆的。

对extract_number四个关键操作的逆向函数：

def inverse_right(res, shift, bits=32):tmp = resfor i in range(bits // shift):tmp = res ^ tmp >> shiftreturn tmpdef inverse_left(res, shift, bits=32):tmp = resfor i in range(bits // shift):tmp = res ^ tmp << shiftdef inverse_right_mask(res, shift, mask, bits=32):tmp = resfor i in range(bits // shift):tmp = res ^ tmp >> shift & maskreturn tmpdef inverse_left_mask(res, shift, mask, bits=32):tmp = resfor i in range(bits // shift):tmp = res ^ tmp << shift & maskreturn tmp

从而可以根据一个随机数直接逆向出一个状态：

def get_one_state(y):y = inverse_right(y, 18)y = inverse_left_mask(y, 15, 4022730752)y = inverse_left_mask(y, 7, 2636928640)y = inverse_right(y, 11)return _int32(y)

如果能得到连续且完整的624个随机数，即可以恢复出MT19937内部的所有状态，从而能克隆出一个完全一致的随机函数。关于这一逆向，已经有较成熟的开源实现randcrack：https://github.com/tna0y/Python-random-module-cracker

randcrack的代码看起来还是很优雅的，但我对这个模块设计有点奇怪的是，它竟然没有提供一个克隆的random，虽然很简单。所以一般这样使用更舒适：

from randcrack import RandCrack as _RandCrack
from random import Randomclass RandCrack(_RandCrack):def __init__(self):super().__init__()def get_random(self):state = []for i in self.mt[:624]:b = ''for j in i:b += str(j)state.append(int(b, 2))rand = Random()rand.setstate((3, tuple(state+[0]), None))return randrc = RandCrack()
r = Random()for i in range(624):rc.submit(r.getrandbits(32))my_rand = rc.get_random()for i in range(1000):assert r.getrandbits(32) == my_rand.getrandbits(32), f"index: {i}"

4.基于z3的MT19937的内部状态求解

在不逆向算法的前提下，也可以利用z3直接进行求解：

from z3 import *
def solve_one_state(out):y1 = BitVec('y1', 32)y2 = BitVec('y2', 32)y3 = BitVec('y3', 32)y4 = BitVec('y4', 32)y = BitVecVal(out, 32)s = Solver()equations = [y2 == y1 ^ (LShR(y1, 11)),y3 == y2 ^ ((y2 << 7) & 0x9D2C5680),y4 == y3 ^ ((y3 << 15) & 0xEFC60000),y == y4 ^ (LShR(y4, 18))]s.add(equations)s.check()return s.model()[y1].as_long()

2.连续输出存在截断的情况下z3的求解部分内部状态

2.1 原理

假设连续输出若干个伪随机数 p 1 , p 2 . . . p 1248 p_{1},p_{2}...p_{1248} p1​,p2​...p1248​，其中， p i p_{i} pi​为16位。由python random模块的底层c源代码[2]可以看出，每个随机数实际是输出随机数的高16位，相当于每个原始输出随机数的截断了一半。
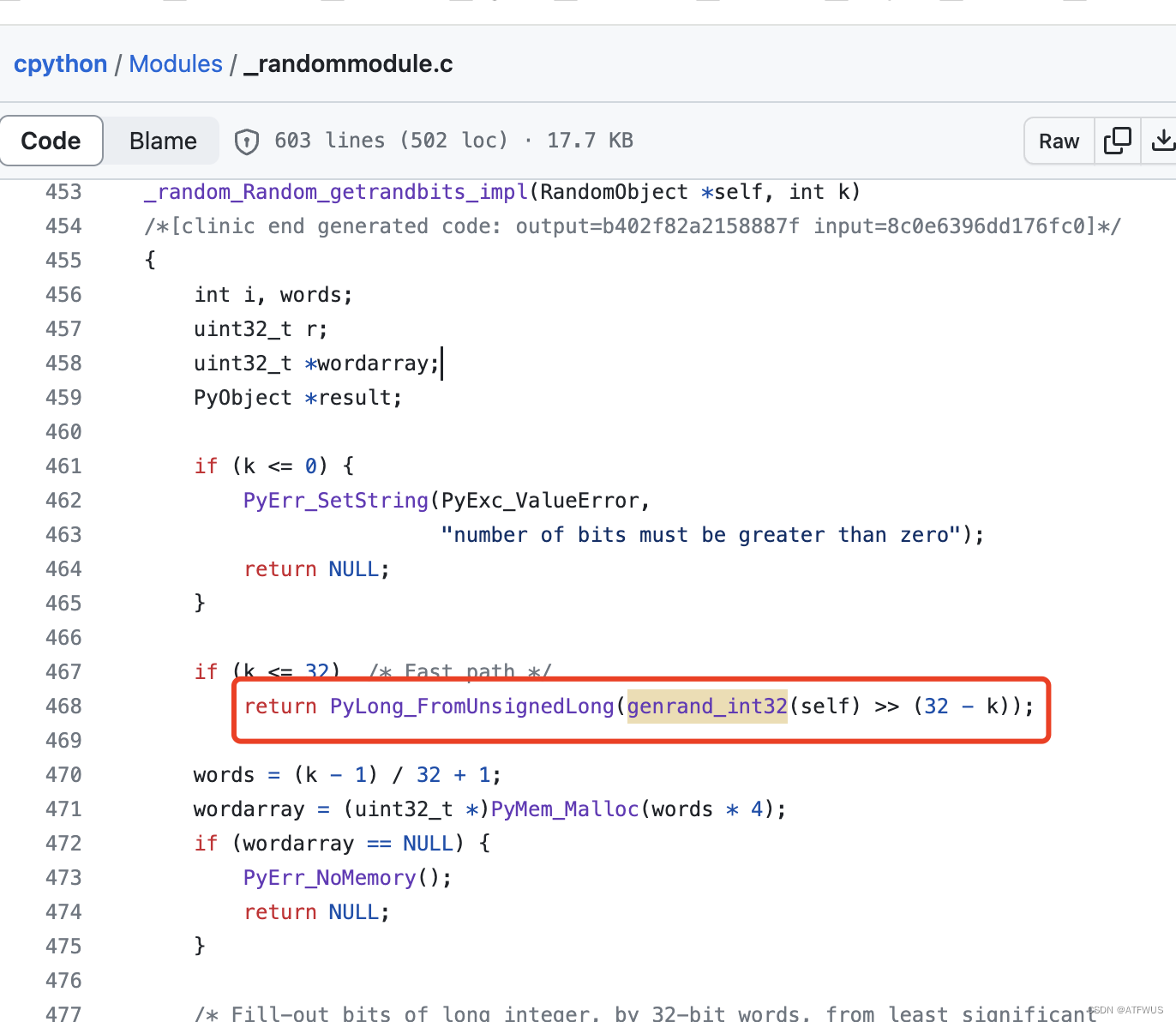
在这里插入图片描述

此时，我们仍然可以利用z3的符号执行去求解可能的内部状态，可以把已知的部分比特位给z3作为约束，尝试求解。因为构造的矩阵是非满秩的，所以得到的状态是满足约束条件的可能解，如果给出的约束足够多，例如上述给出了1248个16位的输出数，也可以得到确定的状态。

例如，假设一个只得到一个随机数的高16位，则可以将其构造为 p i ∣ ∣ ′ ? ′ ∗ 16 p_{i}||'?'*16 pi​∣∣′?′∗16传给相应的解析函数处理，解析函数处理后，将其转为z3中的约束。核心就是使用Extact函数（用于从一个位向量（BitVector）中提取一段连续的比特位）。

def get_one_symbolic(out, index):# 参数检查略out = out.zfill(32)guess_state = BitVec(f'symbolic_guess_{index}', 32)out = out[::-1]for i, bit in enumerate(out):if bit != '?':self.solver.add(Extract(i, i, guess_state) == bit)return guess_state

关于这部分工作，在查找资料的时候发现也有前人做了相应的开源：https://github.com/icemonster/symbolic_mersenne_cracker

2.2 应用一：完全推导内部状态

在上述symbolic_mersenne_cracker项目中给出的test，就是一个完全推导内部状态的例子：

def test():'''This test tries to clone Python random's internal state, given partial output from getrandbits'''r1 = Random()ut = Untwister()for _ in range(1337):random_num = r1.getrandbits(16)#Just send stuff like "?11????0011?0110??01110????01???"#Where ? represents unknown bitsut.submit(bin(random_num)[2:] + '?'*16)r2 = ut.get_random()for _ in range(624):assert r1.getrandbits(32) == r2.getrandbits(32)logger.debug('Test passed!')

通过1248个16位的随机数，能完全恢复内部的状态，从而克隆出一个完全等价的伪随机数生成器。

2.3 应用二：部分推导，复原部分历史随机数生成

修改Untwister模块获取random的代码，改为恢复成给定seed后的状态（默认是给出后面输出的状态）：

主要修改点为，参考[3]：

  • seed后的index为N=624。
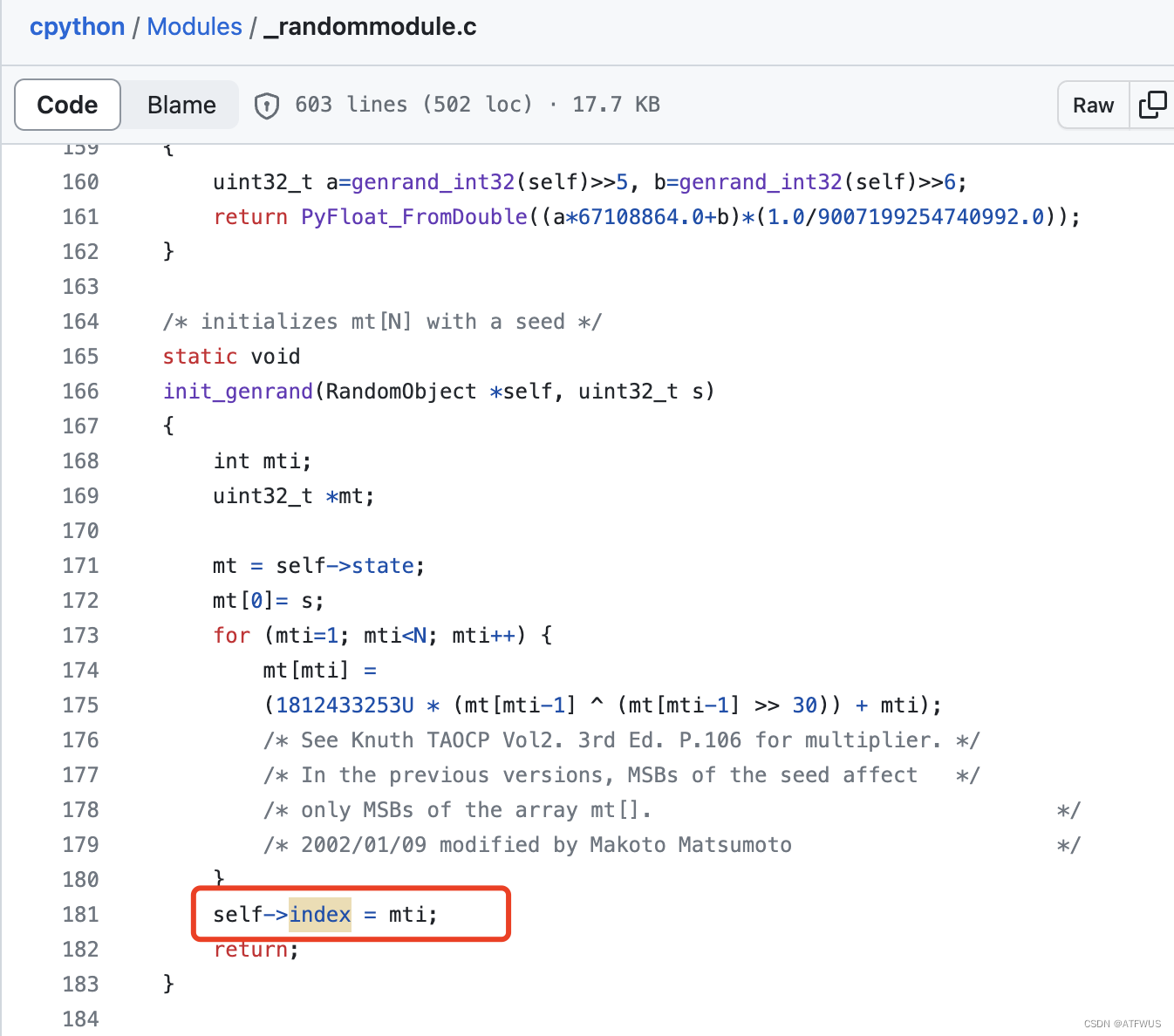
    在这里插入图片描述
  • seed后的第一个state为0x80000000。
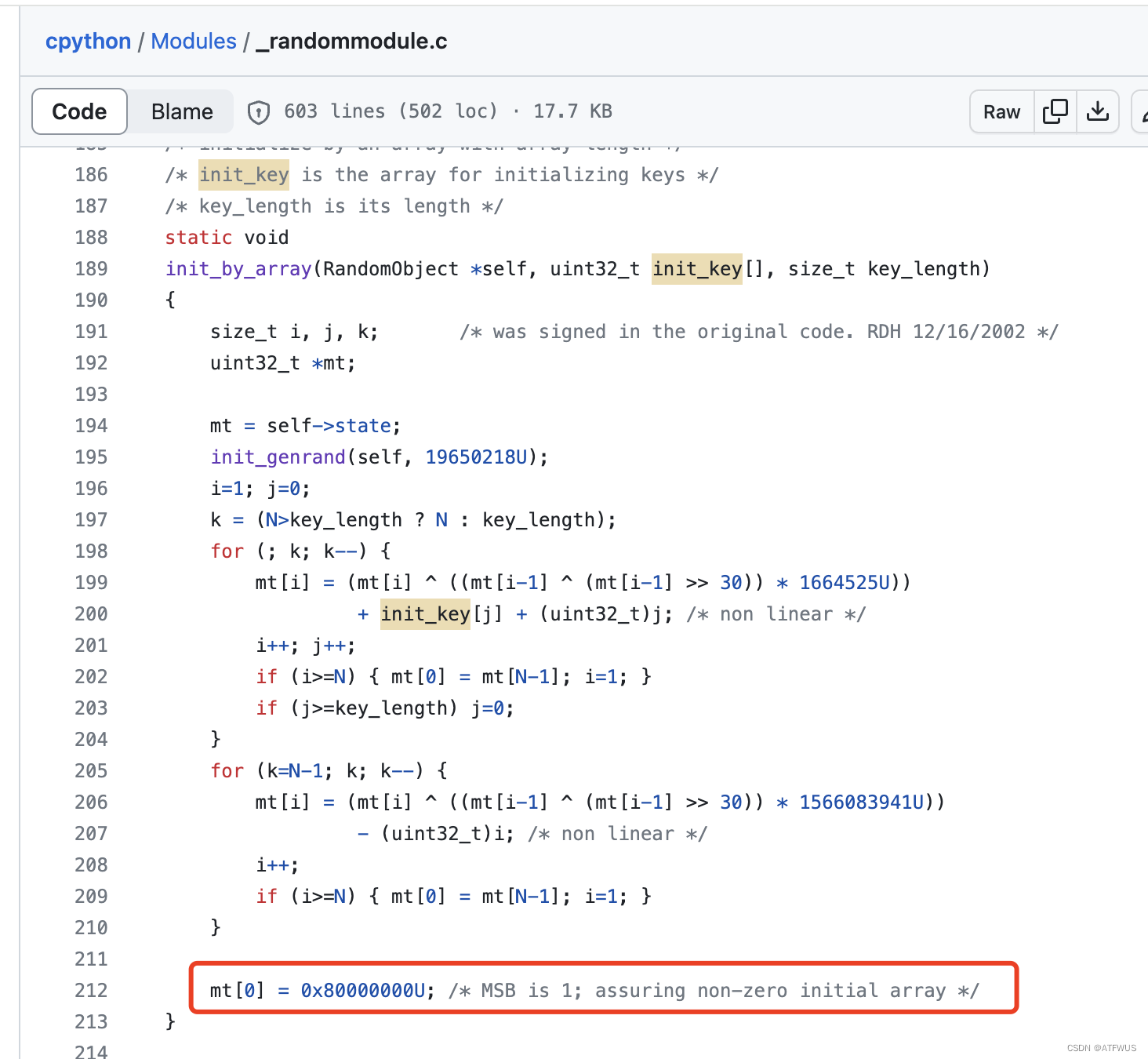
    在这里插入图片描述
from untwister import Untwister as _Untwister
class Untwister(_Untwister):def __init__(self):super().__init__()self.first_MT = self.MTself.index = 624def get_random(self):self.solver.add(self.first_MT[0] == 0x80000000)self.solver.check()model = self.solver.model()state = [model[x].as_long() if model[x] is not None else 0for x in self.first_MT]result_state = (3, tuple(state+[624]), None)rand = random.Random()rand.setstate(result_state)return rand

这样得到random就是seed后的 random，能够复原部分历史的随机数生成：

ut = Untwister()
r1 = random.Random()
my_r = [r1.randint(0, 6) for i in range(666)]for i in my_r:res = bin(i)[2:].zfill(3) + "?" * 29ut.submit(res)ut_rand = ut.get_random()for i in my_r:assert i == ut_rand.randint(0, 6)

3.生成等价种子

在只得到部分截断连续随机数输出的条件下，想完整的恢复种子是不太可能的，但是可以分析random模块种子的初始化过程，从而生成一个与原始种子不相同，但播种后后续部分输出相同的种子。

分析random底层seed相关的初始化部分：

/* initializes mt[N] with a seed */
static void
init_genrand(RandomObject *self, uint32_t s)
{int mti;uint32_t *mt;mt = self->state;mt[0]= s;for (mti=1; mti<N; mti++) {mt[mti] =(1812433253U * (mt[mti-1] ^ (mt[mti-1] >> 30)) + mti);/* See Knuth TAOCP Vol2. 3rd Ed. P.106 for multiplier. *//* In the previous versions, MSBs of the seed affect   *//* only MSBs of the array mt[].                                *//* 2002/01/09 modified by Makoto Matsumoto                     */}self->index = mti;return;
}/* initialize by an array with array-length */
/* init_key is the array for initializing keys */
/* key_length is its length */
static void
init_by_array(RandomObject *self, uint32_t init_key[], size_t key_length)
{size_t i, j, k;       /* was signed in the original code. RDH 12/16/2002 */uint32_t *mt;mt = self->state;init_genrand(self, 19650218U);i=1; j=0;k = (N>key_length ? N : key_length);for (; k; k--) {mt[i] = (mt[i] ^ ((mt[i-1] ^ (mt[i-1] >> 30)) * 1664525U))+ init_key[j] + (uint32_t)j; /* non linear */i++; j++;if (i>=N) { mt[0] = mt[N-1]; i=1; }if (j>=key_length) j=0;}for (k=N-1; k; k--) {mt[i] = (mt[i] ^ ((mt[i-1] ^ (mt[i-1] >> 30)) * 1566083941U))- (uint32_t)i; /* non linear */i++;if (i>=N) { mt[0] = mt[N-1]; i=1; }}mt[0] = 0x80000000U; /* MSB is 1; assuring non-zero initial array */
}

用python分别实现：

from z3 import *
prng_N = 624def u32(x):return x & 0xffffffffdef init_genrand(s):mt = [0 for _ in range(prng_N)]mt[0] = BitVecVal(s, 32)mti = 1while mti < prng_N:mt[mti] = u32(1812433253 * (mt[mti-1] ^ LShR(mt[mti-1], 30)) + mti        )mti += 1return mt, mtidef init_by_array(init_key):key_length = len(init_key)mt, mti = init_genrand(19650218)i, j = 1, 0k = prng_N if prng_N > key_length else key_lengthwhile k:mt[i] = u32((mt[i] ^ ((mt[i-1] ^ LShR(mt[i-1], 30)) * 1664525)) + init_key[j] + j)i, j = i + 1, j + 1if i >= prng_N:mt[0] = mt[prng_N-1]i = 1if j >= key_length:j = 0k -= 1k = prng_N - 1while k:mt[i] = u32((mt[i] ^ ((mt[i-1] ^ LShR(mt[i-1], 30)) * 1566083941)) - i)i += 1if i >= prng_N:mt[0] = mt[prng_N-1]i = 1k -= 1mt[0] = 0x80000000return mt

可以发现random模块的流程：

  • 如果输入的种子是一个小于32位的数，就会直接把这个种子作为mt[0]，然后生成后续的所有状态。
  • 如果输入的种子是一个大于32位的书，就会把输入的种子变成一个数组init_key，每个数组是一个32位数，用这个数组进行一些位操作得到最终的状态，并把第一个状态设置为0x80000000。

假设我们依据2.3得到了一组可能得初始状态（seed后的）init_rand_state，那么我们要构造一个等价种子，使得播种后能产生指定的输出，思路如下：

  • 将种子设为长为624的z3向量数组seed_vecs。
  • 用python重写底层c的init_by_array和init_genrand函数。
  • 将向量数组传入init_by_array函数中参与运算。
  • 将这些参与运算完后的向量与init_rand_state做等价约束传入z3中。
  • z3解方程，得到可能得seed_vecs。
  • 将seed_vecs拼接成一个大数，传入python的random模块中。

通过这些步骤，能得到满足上述要求的种子。代码如下：

def recover_seed(outputs):ut = Untwister()for output in outputs:ut.submit(output)ut_rand = ut.get_random()ut_rand_state = ut_rand.getstate()[1][:-1]seed_vecs = [BitVec(f"seed_{i}", 32) for i in range(624)]seed_rand_state = init_by_array(seed_vecs)s = Solver()for a, b in zip(seed_rand_state, ut_rand_state):s.add(a == b)s.check()model = s.model()seed_init_key = [model[x].as_long() if model[x] is not None else 0for x in seed_vecs]seed_rand_seed = sum([x * (2 ** (idx * 32))for idx, x in enumerate(seed_init_key)])return seed_rand_seed

4.完整代码及工具封装

有关直接对MT19937逆向的代码在第1章已经完全给出，这里仅给出涉及符号执行的代码。

from random import Random
from untwister import Untwister as _Untwister
from z3 import *
from randcrack import RandCrack as _RandCrackprng_N = 624def u32(x):return x & 0xffffffffdef init_genrand(s):mt = [0 for _ in range(prng_N)]mt[0] = BitVecVal(s, 32)mti = 1while mti < prng_N:mt[mti] = u32(1812433253 * (mt[mti-1] ^ LShR(mt[mti-1], 30)) + mti# 1812433253 * (mt[mti-1] ^ (mt[mti-1] >> 30)) + mti)mti += 1return mt, mtidef init_by_array(init_key):key_length = len(init_key)mt, mti = init_genrand(19650218)i, j = 1, 0k = prng_N if prng_N > key_length else key_lengthwhile k:mt[i] = u32((mt[i] ^ ((mt[i-1] ^ LShR(mt[i-1], 30)) * 1664525)) + init_key[j] + j)i, j = i + 1, j + 1if i >= prng_N:mt[0] = mt[prng_N-1]i = 1if j >= key_length:j = 0k -= 1k = prng_N - 1while k:mt[i] = u32((mt[i] ^ ((mt[i-1] ^ LShR(mt[i-1], 30)) * 1566083941)) - i)i += 1if i >= prng_N:mt[0] = mt[prng_N-1]i = 1k -= 1mt[0] = 0x80000000return mtclass RandCrack(_RandCrack):def __init__(self):super().__init__()def get_random(self):state = []for i in self.mt[:624]:b = ''for j in i:b += str(j)state.append(int(b, 2))rand = Random()rand.setstate((3, tuple(state+[0]), None))return randclass Untwister(_Untwister):def __init__(self):super().__init__()self.first_MT = self.MTself.index = 624def get_random_init(self):self.solver.add(self.first_MT[0] == 0x80000000)print(self.solver.check())model = self.solver.model()state = [model[x].as_long() if model[x] is not None else 0for x in self.first_MT]result_state = (3, tuple(state+[624]), None)rand = Random()rand.setstate(result_state)return randdef recover_seed(outputs):ut = Untwister()for output in outputs:ut.submit(output)ut_rand = ut.get_random_init()ut_rand_state = ut_rand.getstate()[1][:-1]seed_vecs = [BitVec(f"seed_{i}", 32) for i in range(624)]seed_rand_state = init_by_array(seed_vecs)s = Solver()for a, b in zip(seed_rand_state, ut_rand_state):s.add(a == b)s.check()model = s.model()seed_init_key = [model[x].as_long() if model[x] is not None else 0for x in seed_vecs]seed_rand_seed = sum([x * (2 ** (idx * 32))for idx, x in enumerate(seed_init_key)])return seed_rand_seed# 根据部分输出恢复可能的种子
def test_recover_seed():# 预设初始种子my_seed = 1173791373my_rand = Random(my_seed)my_outputs = [my_rand.randint(0, 6) for i in range(1000)]my_outputs_sym = [bin(i)[2:].zfill(3) + '?' * 29 for i in my_outputs]guess_seed = recover_seed(my_outputs_sym)guess_rand = Random(guess_seed)assert my_seed != guess_seed# testfor i in range(1000):assert my_outputs[i] == guess_rand.randint(0, 6)print("test recover seed pass!")def test_randcrack():rc = RandCrack()r = Random()for i in range(624):rc.submit(r.getrandbits(32))my_rand = rc.get_random()for i in range(1000):assert r.getrandbits(32) == my_rand.getrandbits(32), f"index: {i}"print("test randcrack pass!")def test_ut():ut = Untwister()r1 = Random()my_r = [r1.randint(0, 6) for i in range(666)]for i in my_r:res = bin(i)[2:].zfill(3) + "?" * 29ut.submit(res)ut_rand = ut.get_random_init()for i in my_r:assert i == ut_rand.randint(0, 6)print("test Untwister pass!")if __name__ == '__main__':test_randcrack()test_ut()#test_recover_seed()

上述代码的能力：

  • 1.若得到完整且连续的624个随机数，使用randcrack即可得到一个完全克隆的random。
  • 2.若得到不完整且连续的若干个随机数（数量很大），使用Untwister有概率能恢复完整的内部状态。
  • 3.若得到不完整且连续的若干个随机数（数量不大），使用Untwister的get_random_init能恢复seed后的状态，能够复原历史的随机数生成。
  • 4.在3的基础上，能够恢复一个种子，该种子在seed后能重现给定随机数的生成。

后续考虑封装成pip工具包… 但是封装成工具包涉及易用性和容错性的问题，貌似工作量不小。

参考

  • [1] https://zh.wikipedia.org/zh-hans/%E6%A2%85%E6%A3%AE%E6%97%8B%E8%BD%AC%E7%AE%97%E6%B3%95
  • [2] https://github.com/python/cpython/blob/3.8/Modules/_randommodule.c
  • [3] https://imp.ress.me/blog/2022-11-13/seccon-ctf-2022#janken-vs-kurenaif

这篇关于MT19937在连续输出存在截断的情况下利用z3符号执行推导内部状态以及等价种子的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/383806。

相关文章

Flutter监听当前页面可见与隐藏状态的代码详解

Flutter监听当前页面可见与隐藏状态的代码详解

《Flutter监听当前页面可见与隐藏状态的代码详解》文章介绍了如何在Flutter中使用路由观察者来监听应用进入前台或后台状态以及页面的显示和隐藏,并通过代码示例讲解的非常详细,需要的朋友可以参考下... flutter 可以监听 app 进入前台还是后台状态，也可以监听当http://www.cppcn
阅读更多...
Spring AI集成DeepSeek实现流式输出的操作方法

Spring AI集成DeepSeek实现流式输出的操作方法

《SpringAI集成DeepSeek实现流式输出的操作方法》本文介绍了如何在SpringBoot中使用Sse（Server-SentEvents）技术实现流式输出,后端使用SpringMVC中的S... 目录一、后端代码二、前端代码三、运行项目小天有话说题外话参考资料前面一篇文章我们实现了《Spring
阅读更多...
Go使用pprof进行CPU,内存和阻塞情况分析

Go使用pprof进行CPU,内存和阻塞情况分析

《Go使用pprof进行CPU,内存和阻塞情况分析》Go语言提供了强大的pprof工具,用于分析CPU、内存、Goroutine阻塞等性能问题,帮助开发者优化程序,提高运行效率,下面我们就来深入了解下... 目录1. pprof 介绍2. 快速上手：启用 pprof3. CPU Profiling：分析 C
阅读更多...
MySQL进阶之路索引失效的11种情况详析

MySQL进阶之路索引失效的11种情况详析

《MySQL进阶之路索引失效的11种情况详析》：本文主要介绍MySQL查询优化中的11种常见情况,包括索引的使用和优化策略,通过这些策略,开发者可以显著提升查询性能,需要的朋友可以参考下... 目录前言图示1. 使用不等式操作符（!=, <, >）2. 使用 OR 连接多个条件3. 对索引字段进行计算操作4
阅读更多...
Rust格式化输出方式总结

Rust格式化输出方式总结

《Rust格式化输出方式总结》Rust提供了强大的格式化输出功能,通过std::fmt模块和相关的宏来实现,主要的输出宏包括println!和format!,它们支持多种格式化占位符,如{}、{:?}... 目录Rust格式化输出方式基本的格式化输出格式化占位符Format 特性总结Rust格式化输出方式
阅读更多...
MySQL 中的服务器配置和状态详解(MySQL Server Configuration and Status)

MySQL 中的服务器配置和状态详解(MySQL Server Configuration and Status)

《MySQL中的服务器配置和状态详解(MySQLServerConfigurationandStatus)》MySQL服务器配置和状态设置包括服务器选项、系统变量和状态变量三个方面,可以通过... 目录mysql 之服务器配置和状态1 MySQL 架构和性能优化1.1 服务器配置和状态1.1.1 服务器选项
阅读更多...
linux进程D状态的解决思路分享

linux进程D状态的解决思路分享

《linux进程D状态的解决思路分享》在Linux系统中,进程在内核模式下等待I/O完成时会进入不间断睡眠状态（D状态）,这种状态下,进程无法通过普通方式被杀死,本文通过实验模拟了这种状态,并分析了如... 目录1. 问题描述2. 问题分析3. 实验模拟3.1 使用losetup创建一个卷作为pv的磁盘3.
阅读更多...
Java实现状态模式的示例代码

Java实现状态模式的示例代码

《Java实现状态模式的示例代码》状态模式是一种行为型设计模式,允许对象根据其内部状态改变行为,本文主要介绍了Java实现状态模式的示例代码,文中通过示例代码介绍的非常详细,需要的朋友们下面随着小编来... 目录一、简介1、定义2、状态模式的结构二、Java实现案例1、电灯开关状态案例2、番茄工作法状态案例
阅读更多...
通过prometheus监控Tomcat运行状态的操作流程

通过prometheus监控Tomcat运行状态的操作流程

《通过prometheus监控Tomcat运行状态的操作流程》文章介绍了如何安装和配置Tomcat,并使用Prometheus和TomcatExporter来监控Tomcat的运行状态,文章详细讲解了... 目录Tomcat安装配置以及prometheus监控Tomcat一. 安装并配置tomcat1、安装
阅读更多...
Linux之进程状态&&进程优先级详解

Linux之进程状态&&进程优先级详解

《Linux之进程状态&&进程优先级详解》文章介绍了操作系统中进程的状态,包括运行状态、阻塞状态和挂起状态,并详细解释了Linux下进程的具体状态及其管理,此外,文章还讨论了进程的优先级、查看和修改进... 目录一、操作系统的进程状态1.1运行状态1.2阻塞状态1.3挂起二、linux下具体的状态三、进程的
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2