本文主要是介绍初赛复习内容,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
内容
信息学比赛
- 全国青少年信息学奥林匹克竞赛(NOI)在 1984 年开始。
- 国际信息学奥林匹克竞赛(IOI)在 1989 年开始。
- 全国青少年信息学奥林匹克联赛(NOIP)在 1995 年开始。
- APIO 在 2007 年开始。
计算机知识
- 寄存器是中央处理器的重要组成部分
- 程序运行时的空间复杂度是指程序运行时理论上所占的内存空间,
- 阶码指明了小数点在数据中的位置。
- Pascal语言,C语言和C++语言都属于 高级语言,编译性语言
- 编译器的主要功能是将源程序翻译成指令
- 存储器有主存和辅存,主存中有ROM和RAM,RAM在关机或停电情况下内容全部丢失,ROM不会。
原码,补码,反码
- 原码:最高位即为符号位( 0 0 0正 1 1 1负),其余位为原来的二进制。
- 反码:正数不变,负数其符号位不变,其余位取反
- 补码:正数不变,负数在其反码的基础上加一。
图像内存,运行内存,各种内存
1 T B = 2 10 G B = 2 20 M B = 2 3 0 K B = 2 40 B y t e 1TB=2^{10}\rm{GB}=2^{20}\rm{MB}=2^30 \rm{KB}=2^{40} \rm{Byte} 1TB=210GB=220MB=230KB=240Byte, 1 B y t e = 8 B i t 1\rm{Byte}=8\rm{Bit} 1Byte=8Bit,其中 B y t e \rm{Byte} Byte为字节, B i t \rm{Bit} Bit为位。
设图片分辨率为 x × y x\times y x×y, z z z位色,则内存为
x ⋅ y ⋅ z B i t x\cdot y\cdot z \rm{Bit} x⋅y⋅zBit
设某计算机的 C P U CPU CPU和内存之间的地址总线宽度是 x x x位( B i t \rm{Bit} Bit),最多使用的内存为 2 x B y r e 2^x\rm{Byre} 2xByre
前缀,中缀,后缀表达式
假如给式子 a + ( b × c ) − ( d + e ) a+(b\times c)-(d+e) a+(b×c)−(d+e)转化
第一步:按照运算符的优先级对所有的运算单位加括号,式子变成了: ( ( a + ( b ∗ c ) ) − ( d + e ) ) ((a+(b*c))-(d+e)) ((a+(b∗c))−(d+e))
第二步:转换前缀与后缀表达式
- 前缀:把运算符号移动到对应的括号前面,则变成: − ( + ( a × ( b c ) ) + ( d e ) ) -( +(a \times (bc)) + (de)) −(+(a×(bc))+(de)),把括号去掉:于是有前缀式子: − + a × b c + d e -+a\times bc+de −+a×bc+de。
- 后缀:把运算符号移动到对应的括号后面,则变成: ( ( a ( b c ) × ) − ( d e ) + ) − ((a(bc)\times )- (de)+ )- ((a(bc)×)−(de)+)−,把括号去掉:于是有后缀式子 a b c × − d e + − abc\times -de+- abc×−de+− 。
常见排序
| 排序方式 | 平均情况 | 最坏情况 | 稳定性 |
|---|---|---|---|
| 插入排序 | O ( n 2 ) O(n^2) O(n2) | O ( n 2 ) O(n^2) O(n2) | 稳定 |
| 希尔排序 | O ( n 1.3 ) O(n^{1.3}) O(n1.3) | 不稳定 | |
| 冒泡排序 | O ( n 2 ) O(n^2) O(n2) | O ( n 2 ) O(n^2) O(n2) | 稳定 |
| 快速排序 | O ( n log n ) O(n\log n) O(nlogn) | O ( n 2 ) O(n^2) O(n2) | 不稳定 |
| 选择排序 | O ( n 2 ) O(n^2) O(n2) | O ( n 2 ) O(n^2) O(n2) | 不稳定 |
| 堆排序 | O ( n log n ) O(n\log n) O(nlogn) | O ( n log n ) O(n\log n) O(nlogn) | 不稳定 |
| 归并排序 | O ( n log n ) O(n\log n) O(nlogn) | O ( n log n ) O(n\log n) O(nlogn) | 稳定 |
vara:array[1..4] of integer;i, j, temp, n:integer;
beginread(n);for i := 1 to n do read(a[i]);for i := 1 to n dofor j := 1 to n-i doif a[j] > a[j + 1] thenbegintemp := a[j];a[j] := a[j + 1];a[j+1] := temp;end;for i:= 1 to n do write(a[i]);
end.
一个排序,若存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变, 则这个排序稳定,反之则不稳定。
视频,图片格式
常见的视频格式有: r m rm rm, r m v b rmvb rmvb, w m v wmv wmv, a v i avi avi, m p 4 mp4 mp4, 3 g p 3gp 3gp, m k v mkv mkv。
常见的图片格式有: j p g jpg jpg, j p e g jpeg jpeg, g i f gif gif, p n g png png, b m p bmp bmp
排列组合
排列公式
A n m = n ( n − 1 ) ( n − 2 ) … ( n − m + 1 ) = n ! ( n − m ) ! A_{n}^m=n(n-1)(n-2)\dots(n-m+1)=\frac{n!}{(n-m)!} Anm=n(n−1)(n−2)…(n−m+1)=(n−m)!n!
组合公式
C n m = A n m m ! = n ! m ! ( n − m ) ! C_{n}^m=\frac{A_n^m}{m!}=\frac{n!}{m!(n-m)!} Cnm=m!Anm=m!(n−m)!n!
根据这个定义发现的公式
∑ i = 0 n C n i = 2 n \sum_{i=0}^nC_n^i=2^n i=0∑nCni=2n
C n r + C n r + 1 = C n + 1 r + 1 C_n^r+C_n^{r+1}=C_{n+1}^{r+1} Cnr+Cnr+1=Cn+1r+1
有重复元素的排列组合:假设有 m m m个数, n n n个不同的数,分别为 a 1 , a 2 , a 3 , … , a n a_1,a_2,a_3,\dots,a_n a1,a2,a3,…,an,每个数出现次数为 b 1 , b 2 , b 3 , … , b n b_1,b_2,b_3,\dots,b_n b1,b2,b3,…,bn,那么本质不同的全排列方案数有
m ! ∏ i = 1 n b i \frac{m!}{\prod \limits_{i=1}^n b_i} i=1∏nbim!
错排公式,定义 D ( 1 ) = 0 , D ( 2 ) = 1 D(1)=0,D(2)=1 D(1)=0,D(2)=1,则
D ( n ) = ( n − 1 ) [ D ( n − 1 ) + D ( n − 2 ) ] D(n)=(n-1)\left[ D(n-1)+D(n-2)\right] D(n)=(n−1)[D(n−1)+D(n−2)]
卡特兰
C n = ( 2 n ) ! / ( n + 1 ) ! / n ! C_n=(2n)!/(n+1)!/n! Cn=(2n)!/(n+1)!/n!
操作系统
常见电脑操作系统有: W i n d o w s Windows Windows, U N I X UNIX UNIX, X E N I X XENIX XENIX, M a c O S Mac\ \ OS Mac OS
进制转化
R R R进制转十进制,将 ( 3506.2 ) 8 (3506.2)_8 (3506.2)8转化为十进制。
( 3506.2 ) 8 = 6 × 8 3 + 5 × 8 2 + + 0 × 8 1 + 6 × 8 0 + 2 × 8 − 1 = 1862.25 (3506.2)_8\\ \begin{aligned} =& 6\times 8^3+5\times 8^2++0\times 8^1+6\times 8^0+2\times 8^{-1}\\ =&1862.25 \end{aligned} (3506.2)8==6×83+5×82++0×81+6×80+2×8−11862.25
十进制转 R R R进制:将 ( 5.3125 ) 10 (5.3125)_{10} (5.3125)10转化为二进制数,整数部分为 ( 101 ) 2 (101)_2 (101)2,剩下 ( 0.3125 ) 10 (0.3125)_{10} (0.3125)10
( 0.3125 ) 10 0.3125 × 2 = 0.625 0.625 × 2 = 1.25 0.25 × 2 = 0.5 0.5 × 2 = 1 , 0 \begin{aligned} (0.3125)_{10}\\ 0.3125\times 2=& 0.625\\ 0.625\times 2=&1.25\\ 0.25\times 2=&0.5\\ 0.5\times 2=&1,0 \end{aligned} (0.3125)100.3125×2=0.625×2=0.25×2=0.5×2=0.6251.250.51,0
所以 ( 0.3125 ) 10 = ( 0.0101 ) 2 (0.3125)_{10}=(0.0101)_2 (0.3125)10=(0.0101)2
计算机协议
计算机发展历史
第一台电子计算机: E N I A C ENIAC ENIAC
第一台具有储存程序功能的的计算机: E D V A C EDVAC EDVAC
几个电子器件
- 电子管( 1496 ∼ 1958 1496\sim 1958 1496∼1958),第一台这样的计算机是 E N I A C ENIAC ENIAC
- 晶体管( 1958 ∼ 1964 1958\sim 1964 1958∼1964)
- 中小规模集成电路( 1964 ∼ 1975 1964\sim 1975 1964∼1975)
- 大规模,超大规模集成电路( 1975 ∼ n o w 1975\sim now 1975∼now)
逻辑运算
- ¬表示not
- ∧表示and
- ∨表示or
- ⊻或⊕表示xor
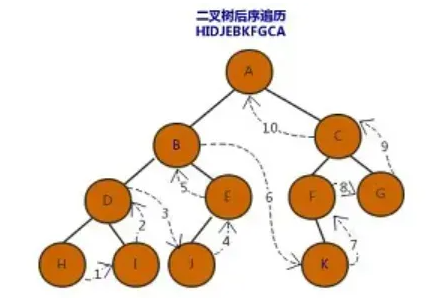
二叉树
完全二叉树指按顺序的二叉树
满二叉树是满的。
语法
@是求一个值的位置,^是这个位置的值。
这篇关于初赛复习内容的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!