1549：最大数——线段树

【题目描述】
原题来自：JSOI 2008

给定一个正整数数列 a1,a2,a3,⋯,an ，每一个数都在 0∼p–1 之间。可以对这列数进行两种操作：

添加操作：向序列后添加一个数，序列长度变成 n+1；

询问操作：询问这个序列中最后 L 个数中最大的数是多少。

程序运行的最开始，整数序列为空。写一个程序，读入操作的序列，并输出询问操作的答案。

【输入】
第一行有两个正整数 m,p，意义如题目描述；

接下来 m 行，每一行表示一个操作。如果该行的内容是 Q L，则表示这个操作是询问序列中最后 L 个数的最大数是多少；如果是 A t，则表示向序列后面加一个数，加入的数是 (t+a)modp。其中，t 是输入的参数，a 是在这个添加操作之前最后一个询问操作的答案（如果之前没有询问操作，则 a=0）。

第一个操作一定是添加操作。对于询问操作，L>0 且不超过当前序列的长度。

【输出】
对于每一个询问操作，输出一行。该行只有一个数，即序列中最后 L 个数的最大数。

【输入样例】
10 100
A 97
Q 1
Q 1
A 17
Q 2
A 63
Q 1
Q 1
Q 3
A 99
【输出样例】
97
97
97
60
60
97
【提示】
样例说明

最后的序列是 97,14,60,96。

数据范围与提示：

对于全部数据，1≤m≤2×105,1≤p≤2×109,0≤t<p。

分析

1. 有关线段树的详细知识，可以参考：线段树蓝书讲解 + 经典例题AcWing 1275. 最大数，讲的非常好，还介绍了，如果题目给了用于建立线段树的初始数组a，应该如何初始化（给data赋值）；
2. 此题属于单点修改、区间查询，单点修改不涉及懒标记，然后这里介绍下四个函数：pushup、bulid、query、modify；

• pushup(u)：由儿子节点信息，计算父亲结点信息，参数u就是当前父亲结点的编号，此题data存区间最大值，所以直接取其左右孩子的区间最大值即可；
• build(u,l,r)：就是建立线段树，u为当前的结点编号，l，r为当前准备分配的区间，先把当前的[l,r]全赋值给父亲u管理，然后我们再把 [l,r]劈开（l+r>>1），一半让u的左孩子管理，另一半让u的右孩子管理；递归建树，当区间只有一个值（l==r），说明分配完毕，那就return；
• query(u,l,r)：查询[l,r]的区间最大值，然后当前想要查询的区间[l,r]和结点u存在三种关系：1. 所查询区间[l,r] 完全覆盖（包含）了 u结点所代表的区间，直接返回当前u的data（因为没必要再去看看哪个孩子管理的[l,r]）；2.所查询区间 [l,r] 和 u的左孩子有交集（l<=mid），那就递归左子树；3. [l,r] 和 u的右孩子有交集（r>=mid+1），那就递归右子树 （当然[l,r]可能和左右孩子都有交集，所以这里就不是else了）
• modify(u,x,v)：x为所要修改的结点编号，v为想要修改的值；那就先从根节点开始找到叶子结点所在位置，找的时候，判断x在u的左孩子，还是右孩子，然后递归找，如果找到（l <= t[u].l && r >= t[u].r）更新他的值，递归完u的左右子树后，通过pushup更新下当前结点u的data；

3. 要分清mid= l + r >> 1 和 mid = t[u].l + t[u].r >> 1，前者是建树的时候，区间拆为两半，来让左右孩子管理；后者为在确定某个结点或某段区间（区间和mid的比较当然是用区间的端点进行比较），是在当前结点u的左子树、还是右子树；

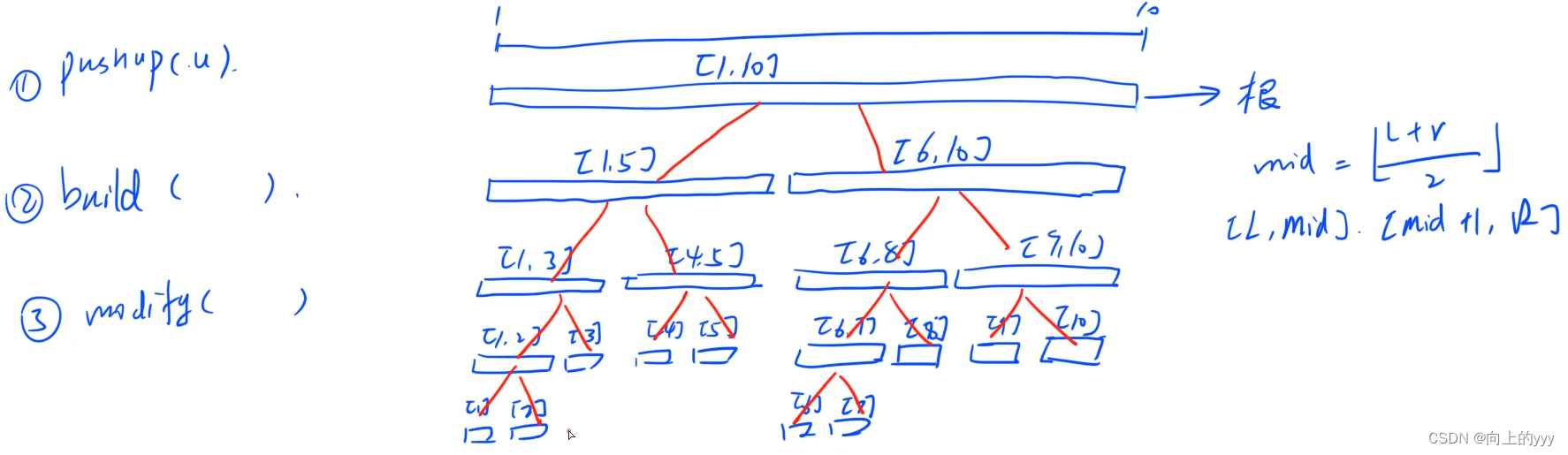
下图为yxc画的线段树的大概结构，以及一些位运算表示的含义；

#include <bits/stdc++.h>using namespace std;const int N = 200010;
struct node {int l, r;int data; //当前区间[l,r]的最大值
};
int m, p;
node t[4 * N];//由儿子节点信息，计算父亲结点信息
void pushup(int u) {//u为当前父亲结点的编号，此题data存最大值t[u].data = max(t[u << 1].data, t[u << 1 | 1].data);
}void build(int u, int l, int r) {//结点编号为u的所代表的区间[l,r]t[u].l = l, t[u].r = r;//叶子结点if (l == r)return;int mid = l + r >> 1;//递归左右子树：左孩子结点编号2*u，区间[l,mid] ;左孩子结点编号2*u+1，区间[mid+1,r]build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
}//1. [l,r] 完全覆盖了 u结点所代表的区间，直接返回当前u的data
//2. [l,r] 和 u的左孩子有交集（l<=mid），那就递归左子树
//3. [l,r] 和 u的右孩子有交集（r>=mid+1），那就递归右子树  （当然可能和左右孩子都有交集，所以这里就不是else了）
int query(int u, int l, int r) {//1.[l,r]包住了结点u的区间if (l <= t[u].l && r >= t[u].r)return t[u].data;int mid = t[u].l + t[u].r >> 1;int res = 0;//2.所查找区间[l,r]和u的左孩子2*u有交集if (l <= mid)res = max(res, query(u << 1, l, r));//3.所查找区间[l,r]和u的右孩子2*u+1有交集，这里是if,不是elseif (r >= mid + 1)res = max(res, query(u << 1 | 1, l, r));return res;
}//先找到叶子结点，从下往上更新; x为所要修改的结点编号，v为想要修改的值
void modify(int u, int x, int v) {//找到叶子结点if (t[u].l == x && t[u].r == x) {t[u].data = v;return;}int mid = t[u].l + t[u].r >> 1;//向u的左孩子方向找叶子结点xif (x <= mid)modify(u << 1, x, v);else //x在u的右孩子modify(u << 1 | 1, x, v);//从下往上回溯更新父亲结点信息pushup(u);
}int main() {cin >> m >> p;int cnt = 0;//当前有效结点（数据）的个数int last = 0;//上一次查询时候得到的结果//建树,根的总区间 [1,m]build(1, 1, m);char op[2];int x;while (m--) {scanf("%s%d", &op, &x);if (op[0] == 'Q') {//查询后x个数last = query(1, cnt - x + 1, cnt);printf("%d\n", last);} else {//把cnt+1的位置的数修改（添加）modify(1, cnt + 1, (last + x) % p);cnt++;}}return 0;
}