山东大学 计算机学院 机器学习与模式识别课程 2019-2020学年 第二学期试卷真题

本文主要是介绍山东大学 计算机学院 机器学习与模式识别课程 2019-2020学年 第二学期试卷真题，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

前言

人工智能班4学分课程试卷
区别于普通班的3学分课程试卷
主要用于学习交流，如要转载或者使用请标明出处
纯手打，如有帮助，麻烦点赞收藏🙏

---

一. 判断题 （24分）

1.(T/F) 假设我们有N个样本，$x_1$,$x_2$…$x_N$.每个样本$x_i\in R^d$.则该样本集合的协方差矩阵S的维度是$N$ x $N$。
2. (T/F) 通过Bootstrap采样获得的训练集可能存在重复的样本。
3. (T/F) 过滤式特征选择方法与模型（model）无关。
4. (T/F) C4.5和CART都是Leo Breman提出的。
5. (T/F) CART算法既可以用来解决分类也可以用来解决回归任务。
6. (T/F) 只要数据集不存在冲突。一棵决策树通常可以完美（100%）拟合训练数据。此时，这棵树的泛化误差也达到了最优值。
7. (T/F) 一棵决策树的不同节点处，不能存在重复子树。
8. (T/F) 集成学习主要分为并行算法和串行算法。其中随机森林属于串行算法，即每一颗树的学习受其他树学习的影响。
9. (T/F) 核函数是将高维空间中的数据映射到低维空间，从而实现对数据的非线性变换。
10. (T/F) 假设$x=[x_1,x_2]$，且$x_1$和$x_2$是相互独立的随机变量，那么$x$的协方差矩阵是对角阵。
11. (T/F) GBDT的基学习都是决策树，所以GBDT会在每一次迭代中(each iteration)增加一棵决策树。
12. (T/F) 如下图所示的KNN的决策边界，我们可以得出$k_1<k_2<k_3$

---

二.简答题 （46分）

1.请你谈谈对过拟合和欠拟合的理解，以及如何缓解过拟合和欠拟合问题（8分）

2.Bagging是常见的集成学习算法。请写出Bagging算法的全称。(2分)

3.请利用最大似然估计（maximum likelihood estimation）得出逻辑回归的目标方程（取$y\in${-1,1}）（8分）

4.假设矩阵A的SVD分解是A = $U\sum V^T$。简述$U$,$\sum$,$V$三个矩阵的结构特性（结合特征分解）。为什么我们更多地使用SVD而不是特征分解来实现PCA。（8分）

5.请写出Huber loss的损失函数。并画出$\delta =1$和$\delta =2$相对应的曲线。(4分)

6.请举例说明超参和模型参数的区别。并简述超参的调节方法（如何选择超参）。（6分）

7.在朴素贝叶斯理论中，我们可以利用样本的频率估计class prior和conditional probability。请根据最大似然估计和二项分布B(N,P)证明其合理性。必要时请给出相关文字解释。（6分）

8.请写出评价指标$F_{\beta }$的公式。在解决实际任务时。如果相比查准率（precision）。我们更看重召回率（recall），那么我们应该令$\beta >1$还是$\beta <1$。（4分）

---

三、综合题（30分）

A.如下一个多分类（multi-class classification）任务的混淆矩阵。请根据该混淆矩阵计算出微查准率（micro-P），微查全率（micro-R），微$F_1$(micro-$F_1$)
宏查准率（macro-P），宏查全率（macro-R），宏$F_1$(macro-$F_1$) (12分)

---

B. 假设我们有5个一维的数据点：$x_1=1,x_2=2,x_3=4,x_4=5,x_5=6$
他们的标签分别是$y_1=1,y_2=1,y_3=-1,y_4=-1,y_5=1$ （8分）

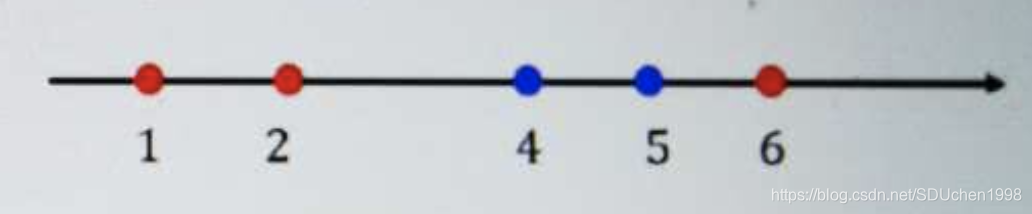
1.对上述五个数据点进行分类，请给出线性SVM的目标函数，并给出在其对偶空间中${\alpha }_1$的目标函数

2.假设使用多项式核函数（polynomial kernel）：K($x_i$,$x_j$)=$(x_i{x}_j+1{)}^2$，惩罚因子C=100。给出线性SVM的目标函数，并给出在其对偶空间中${\alpha }_1$的目标函数。

---

C.针对回归任务，假设数据集T={($x_1$,$y_1$),($x_2$,$y_2$),…,($x_m$,$y_m$)}
$x_i$=[${x_i}^{(1)}$,${x_i}^{(2)}$,…,${x_i}^{(n)}$]${}^T$$\in R^n$
且存在线性模型：f(x)=${\theta }_1{x}^{(1)}+{\theta }_2{x}^{(2)}+...+{\theta }_n{x}^{(n)}+{\theta }_0$ = ${\theta }^{T}x\text{θTx}{\theta }^{T}x$，其中$\theta \text{θ}\theta$ =$[{\theta }_0,{\theta }_1,{\theta }_2,...,{\theta }_n]$${}^T$ （10分）

1.假设采用square loss，请写出具体的损失函数L

2.请根据SGD（Stochastic Gradient Descent）策略和BGD（ Batch Gradient Descent）策略分别写出参数的优化过程与更新策略。

3.在损失函数中引入L1 norm。试给出新的损失函数L,并分析L1 norm的作用。

这篇关于山东大学 计算机学院 机器学习与模式识别课程 2019-2020学年 第二学期试卷真题的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---