本文主要是介绍ARMA 时间序列模型与预测,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
白噪声
可以通过 Box-Ljung 检验来检验序列是否为白噪声:
set.seed(100)
data = rnorm(100)
Box.test(data, type='Ljung', lag = log(length(data)))

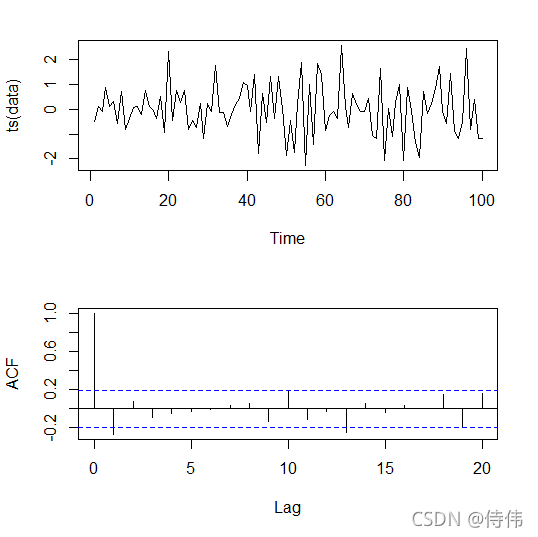
从结果中可以看见 p = 0.09169 > 0.05 p = 0.09169 > 0.05 p=0.09169>0.05,因此无法拒绝序列为白噪声的假设。下面绘制一下该序列的图像以及 ACF 图像:
set.seed(100)
data = rnorm(100)
Box.test(data, type='Ljung', lag = log(length(data)))op <- par(mfrow=c(2, 1), mar=c(5, 4, 2, 2) + .1)
plot(ts(data))
acf(data, main = "")
par(op)
AR(p)序列
先给出一个 AR(2) 的手工计算例子,在这个例子中可以通过 y n − 1 , y n − 2 y_{n-1},y_{n-2} yn−1,yn−2 预测 y n y_n yn
n <- 200
x <- 1:10
f = c(1,2)
y1 = x[1]; y1
y2 = x[2] + f[1] * y1; y2
y3 = x[3] + f[1] * y2 + f[2] * y1; y3
y4 = x[4] + f[1] * y3 + f[2] * y2; y4

实际上也可以通过 filter() 函数来计算:
x = 1:10; x
y = filter(x, c(1, 2), method='r'); y

下面计算一个 p = 3 p=3 p=3 的例子:
n <- 200
x <- rnorm(n)
f = c(.3, -.7, .5)
y <- rep(0, n)
y[1:3] = x[1:3]
for (i in 4:n) {
y[i] <- f[1]*y[i-1] +f[2]*y[i-2] + f[3]*y[i-3] + x[i]
}
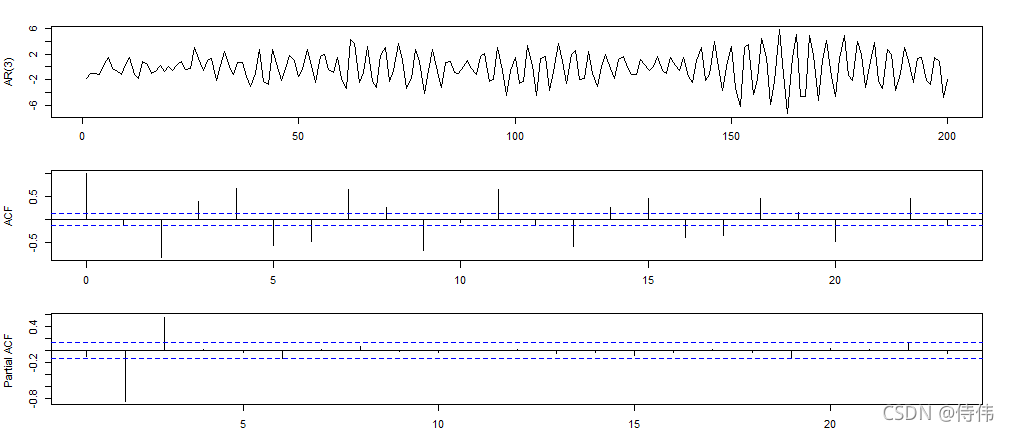
op <- par(mfrow=c(3,1), mar=c(2,4,2,2)+.1)
plot(ts(y), xlab="", ylab="AR(3)")
acf(y, main="", xlab="")
pacf(y, main="", xlab="")
par(op)
同样地,也可以通过 filter() 函数来计算:
y = filter(x, c(.3, -.7, .5), method='r'); y
op <- par(mfrow=c(3,1), mar=c(2,4,2,2)+.1)
plot(ts(y), xlab="", ylab="AR(3)")
acf(y, main="", xlab="")
pacf(y, main="", xlab="")
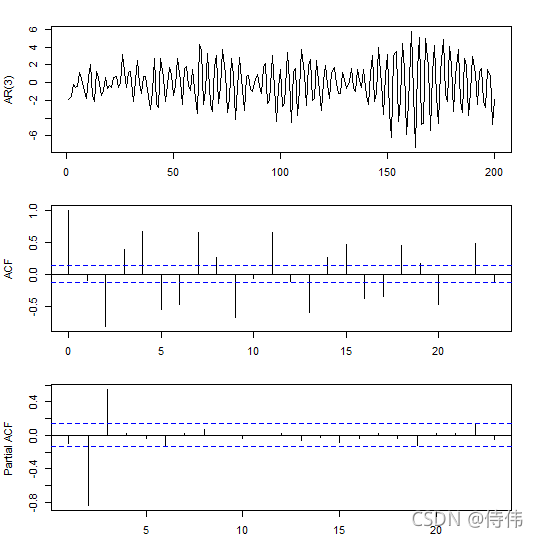
结果是一样的。
MA 模型
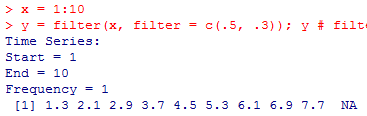
直接使用 filter() 函数计算 MA 模型:
x = 1:10
y = filter(x, filter = c(.5, .3)); y # filter 函数未设置 method,默认为'c',即使用滑动平均
手工计算MA模型代码:
x = 1:10
f = c(.5,.3)
y <- rep(NA, 10)
for (i in 1:9) {
y[i] <- f[1]*x[i+1] + f[2]*x[i]
}
y

结果是一样的。
ARIMA模型
R 语言中自带的 arima.sim() 函数可以模拟生成 AR、MA、ARMA 或 ARIMA 模型的数据。其原型为:
arima.sim(model, n, rand.gen = rnorm, innov = rand.gen(n, ...),n.start = NA, start.innov = rand.gen(n.start, ...),...)
其中,model 是一个列表,用于指定各模型的系数;order 是 ARIMA(p, d, q) 中 ( p , d , q ) (p, d, q) (p,d,q) 三个元素的向量, p p p 为 AR 阶数, q q q 是 MA 的阶数, d d d 是差分阶数。例如,模拟如下的 ARIMA(1, 1, 1) 模型,并产生长度为300的样本:
Y t = X t − X t − 1 , X t = − 0.9 X t − 1 + ε t + 0.5 ε t − 1 , ε t ∼ W N ( 0 , 2 2 ) Y_t = X_t - X_{t-1}, X_t = -0.9X_{t-1} + \varepsilon_t + 0.5\varepsilon_{t-1}, \varepsilon_t \sim WN(0, 2^2) Yt=Xt−Xt−1,Xt=−0.9Xt−1+εt+0.5εt−1,εt∼WN(0,22)
R 语言代码为:
x <- 2.0 * arima.sim(model = list(ar = c(-0.9), ma = c(0.5), order = c(1, 1, 1)), n=300)
ARIMA案例分析
对山西省 2019-2025 年教育人口流出数量进行 ARIMA 时间序列建模,体会ARIMA 建模的整个过程。时间序列分析分为以下五步:
- ARIMA 模型要求序列满足平稳性,查看 ADF 检验结果,根据分析 t 值,分析其是否可以显著地拒绝序列不平稳的假设(p<0.05 或0.01)
- 查看差分前后数据对比图,判断是否平稳(上下波动幅度不大),同时对时间序列进行偏(自相关分析),根据截尾情况估算其 p、q 值
- ARIMA 模型要求模型具备纯随机性,即模型残差为白噪声,查看模型检验表,根据 Q 统计量的 p 值(p 值大于 0.01为白噪声,严格则需大于 0.05)对模型白噪声进行检验,也可以结合信息准则 AIC 和 BIC 值进行分析(越低越好),也可以通过模型残差ACF/PACF 图进行分析
- 根据模型参数表,得出模型公式
- 结合时间序列分析图进行综合分析,得到向后预测的阶数结果
| 年份 | 教育人口流出 |
|---|---|
| 2008年 | 18.57 |
| 2009年 | 19.57 |
| 2010年 | 17.96 |
| 2011年 | 15.74 |
| 2012年 | 13.09 |
| 2013年 | 14.57 |
| 2014年 | 12.76 |
| 2015年 | 11.93 |
| 2016年 | 11.9 |
| 2017年 | 9.56 |
| 2018年 | 8.11 |
| 2019年 | 6.06 |
绘图观察原始序列
library(fUnitRoots)
install.packages('tseries')
library(tseries)
install.packages('forecast')#安装预测用的包
library(forecast)
x=ts(data$教育流出人口,start=2008,end=2019)#将数据转化为时间序列格式
plot(x,type='o')#画图
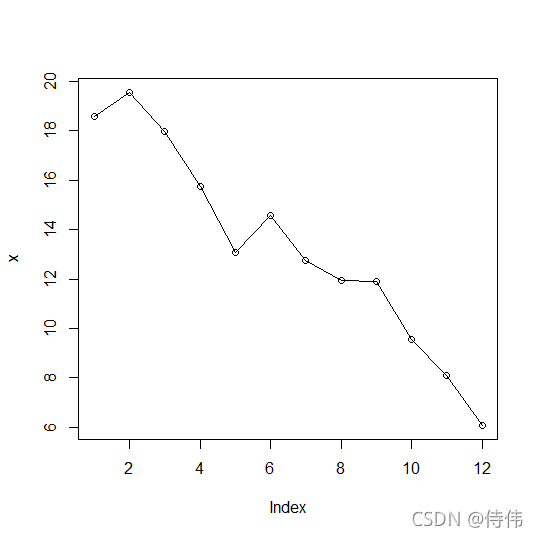
从图上可见,原始时间序列具有趋势性。
平稳性检验
adfTest(x,lags=3,type = c("ct"))

说明原始序列是非平稳的。
对数据作一阶差分处理
dx=diff(x)
plot(dx,type='o')#画图
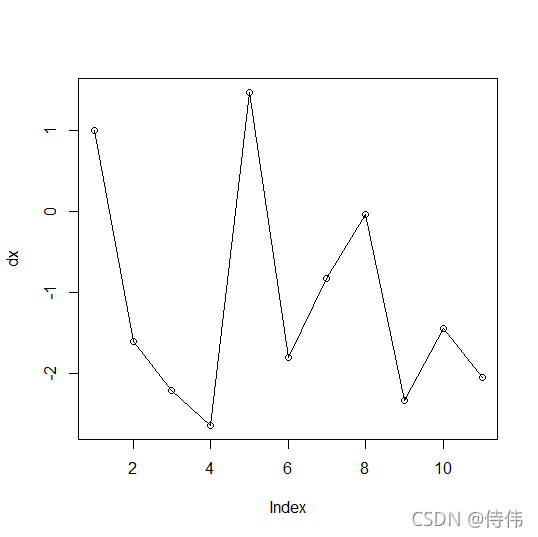
对一阶差分数据进行平稳性检验
adfTest(dx,lags=0,type = c("c"))
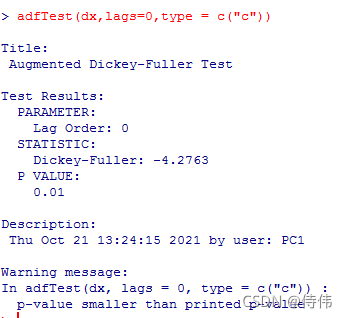
说明一阶差分序列为平稳序列。
确定ARMA阶数
acf(dx)
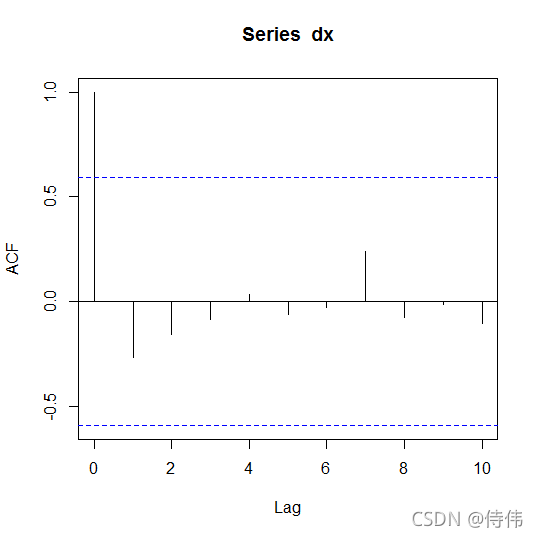
pacf(dx)
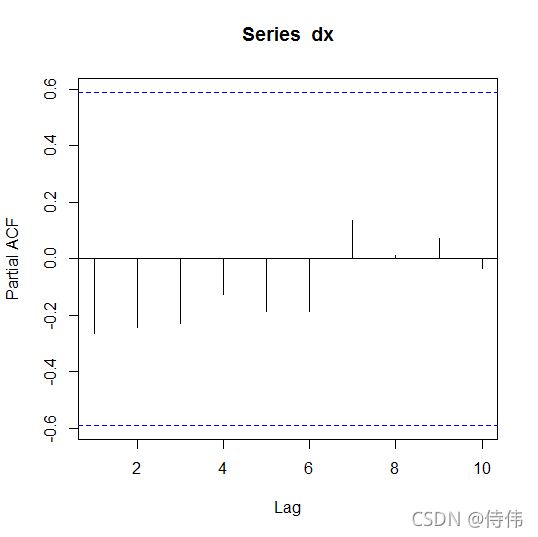
使用auto.arima()自动定阶
library(forecast)
fit=auto.arima(x)
summary(fit)
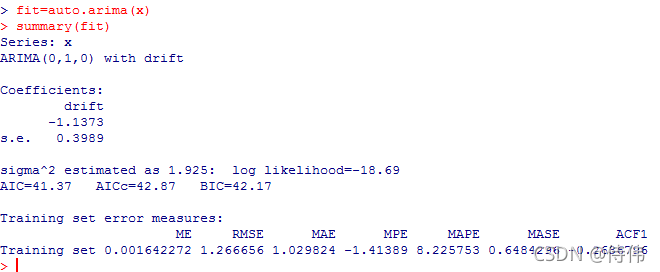
自动定阶为(0,1,0)的ARIMA模型。
残差分析图:
checkresiduals(fit)
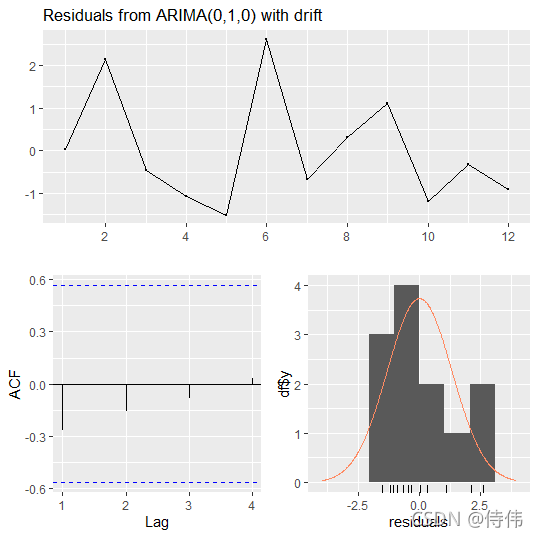
从残差分析图来看,模型的拟合效果并不理想,或许并不十分适合ARIMA模型。
参考资料
Datawhale 开源文档:https://github.com/datawhalechina/team-learning-data-mining/tree/master/TimeSeries
感谢Datawhale对开源学习的贡献!
这篇关于ARMA 时间序列模型与预测的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!









