本文主要是介绍货币凑面值类题目,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
货币凑面值类题目
- 分类,限制/不限制某面值的使用张数,同面值的相同/不同
- 限制/不,相同,差别只在dp每格的枚举数量的个数
- 限制,不同,就每个位置选拿or不拿
- 求答案的种类
- 返回所有方法=》路径,方法数,最少张数
- 返回原数组对应的下标(没看到,//todo)
- 流程都是先排序,分开面值表和对应的张数表
- 优化/剪枝:只要返回最小数量时,用 [[窗口内最大值和最小值的更新结构]]找到最小的张数,省略了枚举。看体系班24课
[[货币凑面值-每张都认为不同]] #从左到右的尝试模型
- 本质上就是 [[背包问题]],背包是在结果集中挑最大值的,凑面值是在结果集中挑结果为固定的值。
- 区别:背包问题中的限制是针对全体,而不是针对某个值的限制
- 题目1:
- arr是货币数组,其中的值都是正数。再给定一个正数aim。
即便是值相同的货币也认为每一张都是不同的,
返回组成aim的方法数
例如:arr = {1,1,1},aim = 2
第0个和第1个能组成2,第1个和第2个能组成2,第0个和第2个能组成2
一共就3种方法,所以返回3 - 返回方法数的答案
- arr是货币数组,其中的值都是正数。再给定一个正数aim。
- 思路:index遍历每个位置选or不选都调递归
- base case:超过aim return 0。index到达末尾,如果value=aim 返回1 否则返回0
- 决策:p1=(index++,value)
- p2=(index++,value+arr[index])
- 返回:p1+p2
- 升级版:返回所有可行的答案排列。
- 区别:返回所有答案需要进行DFS,需要对path加入当前部分,调用函数,恢复现场
- 思路:index遍历每个位置选or不选都调递归
- base case:超过aim return -1,上层处理。index到达末尾,把当前组合加入ansList
- 决策:
- 不要index位置的数
- 直接调用 index++,value
- 把arr[i]加入pathList
- 调用 index++,value+arr[i]
- 在pathList中删除末尾
- 不要index位置的数
[[货币凑面值-限定面值,不限定每种面值的张数]] #从左到右的尝试模型
-
题目:给定数组arr,arr中所有的值都为正数且不重复
每个值代表一种面值的货币,每种面值的货币可以使用任意张
再给定一个整数 aim,代表要找的钱数
求组成 aim 的方法数 -
思路:每个位置都把能使用的张数循环一轮,每次都调index++和相应的rest
-
到每个位置都把rest=rest-arr[i]*当前最大张数,index++
-
限制:rest-arr[i]*当前最大张数>=0
-
base case:index=len。(限制条件使rest不会为0,所以不用考虑rest)
-
决策:根据rest求arr[i]*当前最大张数。for循环张数,调用index++,rest-arr[i]*当前张数
-
代码
-
dp
-
递归过程有枚举行为,改成dp严格表结构后用空间感解决
-

-
优化后
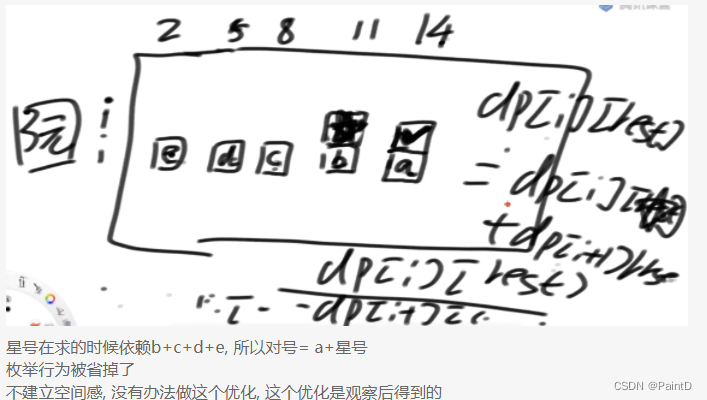
[[货币凑面值-限定面值和每种面值的张数]]#从左到右的尝试模型
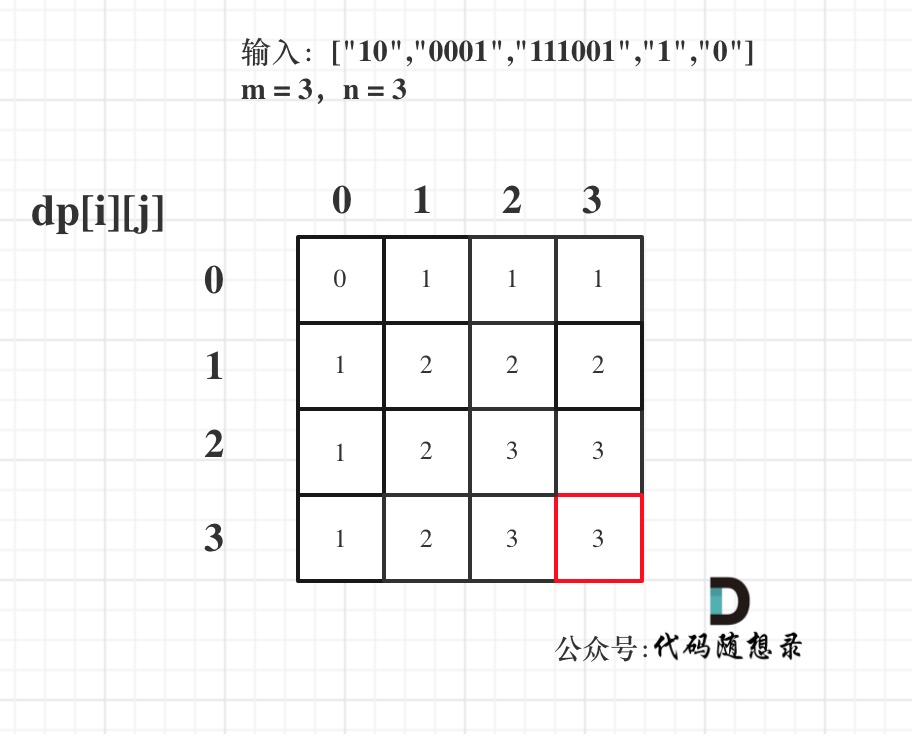
- arr是货币数组,其中的值都是正数。再给定一个正数aim。
每个值都认为是一张货币,
认为值相同的货币没有任何不同,
返回组成aim的方法数
例如:arr = {1,2,1,1,2,1,2},aim = 4
方法:1+1+1+1、1+1+2、2+2
一共就3种方法,所以返回3 - 问题一、一共有几种组成的方法
- 问题二、最小需要几张
这篇关于货币凑面值类题目的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!