本文主要是介绍堆排序(建堆及向下调整),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
首先,堆排序顾名思义,它的数据存储的像一个堆一样,那么想一下,像堆的数据类型都有什么?
树形结构!
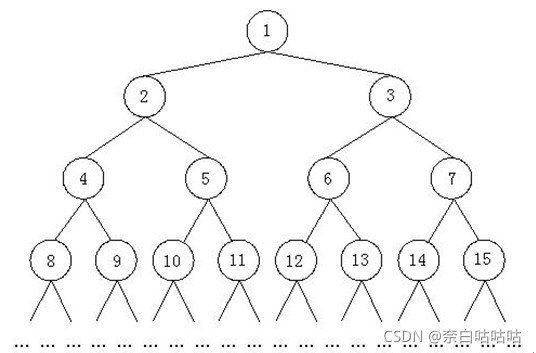
所以,堆排序的存储就是通过一颗完全二叉树实现的,可以理解成满了,但没完全满 为什么这样说,原因很简单,它的n-1层组成的二叉树必须是满二叉树,但是叶子结点组成的第n层可以不满,但是有一个前提条件
假设根节点编号为1,两个子节点为2,3,那么2和3的子节点空余的顺序必须有序,就是说,4,5,6这三个叶子结点必须满足按顺序(也即是说,若6这个叶子结点存在,那么前面的说有叶子结点不可以空缺)
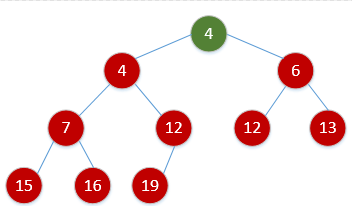
讲完了基本的概念,考虑他的分类和操作,它的分类• 大根堆每个结点的权值都比儿子的权值大• 小根堆• 每个结点的权值都比儿子的权值小
• 堆的性质—>大根堆的根结点一定权值最大,小根堆的根结点一定权值最
堆排序与普通的排序一样,有构建,插入,删除,维护的三种操作,但是,他是稳定的排序最坏的情况的复杂度为N(nlogn),若n的大小不是很大,可以视为N(n)
建堆:
•现在我们有一个数组a[1…n],如何把它初始化成一个堆?
从编号大的点,到编号小的点,依次进行“筛选”操作。就是实现一个简单的“sort”
所谓“筛选”指的是,对一棵左/右子树均为堆的完全二叉树,“调整”根结点使整个二叉树也成为一个堆。
通俗一点,就是说,在我调整根节点的同时,我将本来无序的二叉树变成一颗有序的二叉树
重点来了!我们需要一个东西来帮助我们实现“筛选”,这里引进两个概念——向上调整,向下调整
向下调整:
• 假设有一个堆heap[1…n],我现在要删除第一个元素(最大的元素),如何维护堆的性质不变?
将根节点删除(后面讲),把最后一个点与根节点交换,若当前的点比左右儿子中任意一个小,那么就交换他们(若两个儿子都比当前节点大,那么取更大的那个交换!)
代码:
//举例一个小根堆
void heap_adjust(int x) {//随便写个名字,x为当前节点的下标
while (x*2<=tot) {//判断是否越界,tot指的是总结点数
int j=x*2;//int一个j假设左儿子更大
if (x*2+1<=tot&&heap[x*2+1]<heap[x*2])j++;//判断左儿子大or右儿子大
if (heap[j]<heap[x])swap(heap[x],heap[j]),x=j;//如果当前节点大于根节点,交换
else break;//不行就结束,说明这个堆有序
}
}
这是一个向下调整的操作,我们用向下调整初步建立堆
假设一个堆heap[1.2.3…99],每次对第一个未知是否子树有序的节点进行向下调整,这样就完成了一个初步的建堆

合理的不行!
要从后往前依次做操作,为什么这样是对的?因为它是对的 因为你每一次操作能保证他和他的左右儿子是有序的,所以当到根节点的操作时,他的左右子树一定是有序的(tot/2代表第一个非叶子节点)
————————————
这篇关于堆排序(建堆及向下调整)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!