本文主要是介绍从零开始强化学习一:Bandit Problem,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
一:强化学习概述
强化学习是一种机器学习方法,旨在让智能体在与环境交互的过程中学会制定最优策略,以达到最大化累积奖励的目标。
在强化学习中,智能体需要学会从环境中感知状态,做出动作,并通过环境返回的奖励信号来更新自己的策略。通常情况下,智能体需要通过不断地尝试和反馈来优化策略,直到最终达到最优策略。
强化学习的关键概念包括:
智能体(Agent):类似动作执行者,游戏玩
环境(Environment):智能体在任意时刻所处的环境。
动作(Action):智能体在某个状态下采取的行动。
报酬(Reward):智能体在采取某个动作后,从环境中获得的奖励信号。
Q值函数(q(A)=E(R|A)):描述了在某个状态下采取某个动作后所能获得的累积奖励期望值。
强化学习算法包括:Q学习、SARSA、Actor-Critic、深度Q网络(DQN)等等。这些算法都采用了不同的方法来实现智能体的决策过程,并通过不断地学习和优化来实现最优策略的选择。强化学习在许多领域有着广泛的应用,例如自动驾驶、机器人控制、游戏AI等。
废话不多说,下面开始实战:
二:Bandit Problem(赌博机问题)
Bandit Problem(赌博机问题)是强化学习中的一个经典问题,它是指一个智能体需要在多个赌博机中选择一个赌博机进行游戏,每个赌博机有不同的奖励概率分布,智能体需要通过不断地尝试不同的赌博机,从而获得最大的累计奖励。
在 Bandit Problem 中,每个赌博机可以看作是一个“臂”,智能体可以通过拉动臂来尝试不同的赌博机。每次拉动一个赌博机,智能体会得到该赌博机对应的奖励,奖励通常是一个随机变量,其概率分布通常是未知的。因此,智能体需要通过不断地尝试不同的赌博机,来估计每个赌博机的奖励概率分布,并选择那些估计奖励最高的赌博机。
Bandit Problem 可以有多种变体,包括 k-臂赌博机问题、非定态赌博机问题、上下文赌博机问题等。这些变体中,上下文赌博机问题是一种比较常见的形式,它引入了关于赌博机的额外信息,例如赌博机的特征向量、当前状态等,从而使得智能体能够更准确地估计每个赌博机的奖励概率分布,进而做出更好的选择。
下面以Bandit Problem原理入门强化学习
现在有数量不知的赌博机,每个赌博机有不同的特性(即猜中和不猜中),假设玩家现在决定玩赌博机1000次,最初的情况是玩家不知道每个赌博机的能否猜中的情况,而是要先玩了之后,根据结果去推断赌博机是否是好的赌博机(即中奖多的)。
那么什么是好的赌博机呢?
假设现在有两个赌博机a,b,能得到硬币枚数和对应该率如下表:
| slot machine a | ||||
| 能得到硬币枚数 | 0 | 1 | 5 | 10 |
| 概率 | 0.7 | 0.15 | 0.12 | 0.03 |
| slot machine b | ||||
| 能得到硬币枚数 | 0 | 1 | 5 | 10 |
| 概率 | 0.5 | 0.4 | 0.09 | 0.01 |
那么我们可以很容易联想到用期望去衡量:
a:E(a) = 0*0.7+1*0.15+5*0.12+10*0.03=1.05
b:E(b) = 0*0.50+1*0.4+5*0.09+10*0.01=0.95
期望代表平均,那么玩1000次,要收获硬币最多,自然选择slot machine a啦。
以上面例子来说:
报酬(Reward)可以说是能得到硬币枚数,R={0,1,5,10};Agent是玩家;Action是玩家能采取的行动,也就是选slot machine a或者slot machine b,即变量是A = {a,b};那么选择A后得到报酬的E(R|A),也就是我们说的行动价值Q(A)=E(R|A)
三:赌博机算法
假设赌博机a,b实验三回后能得到的枚数如下:
| slot machine | 结果 | ||
| 第1回 | 第2回 | 第3回 | |
| a | 0 | 1 | 5 |
| b | 1 | 0 | 0 |
Q(a)=(0+1+5)/3=2,Q(b)=(1+0+0)/3=0.33
实验n回 ,
代码:
import numpy as np# naive implementation
np.random.seed(0)
rewards = []for n in range(1, 11):reward = np.random.rand()rewards.append(reward)Q = sum(rewards) / nprint(Q)但是这样子不是太聪明,我们先注重第n-1次时的行动价值推定:
第n-1回:,......(1)
第n回:.......(2)
将(1)式代(2)式:
化简一下:
看上面的式子,也就是说第n回实在n-1回的基础上,再加上更新项而来,也就是Q(n-1)在更新成Q(n)时是按Rn的方向前进,
是学习率。
代码:
np.random.seed(0)
Q = 0for n in range(1, 11):reward = np.random.rand()Q = Q + (reward - Q) / nprint(Q)玩家策略:
e-greedy是一种在强化学习中常用的动作选择策略。它可以平衡探索和利用的关系,旨在在不断学习的过程中找到最优策略。
e-greedy策略的基本思想是,智能体在每个时间步根据一定的概率选择最优的动作,或者随机选择其他动作以探索未知的状态和动作空间。具体来说,e-greedy策略的动作选择过程如下:
-
在每个时间步,以概率ε(0 <= ε <= 1)随机选择一个动作,以探索未知的状态和动作空间;
-
在以1-ε的概率选择最优动作,以利用已有的知识和经验;
e-greedy策略中的ε被称为探索率,探索率越大,智能体越倾向于探索未知的状态和动作空间,探索率越小,智能体越倾向于利用已有的知识和经验。在实际应用中,ε的值可以根据具体问题的特点和需要进行调整。
像上面的赌博机a,b一样,第1回,a是0,b是1,按greedy策略,一直选最好的slot就行了,那么之后就一直选b,但是实际上a可能是最好的slot。这样的问题,是slot价值推定中有不确定性。所以,玩家要减少不确定性,提高信赖度。e-greedy是平衡利用现有经验和探索之间的度。
四:10-赌博机代码
定义10个赌博机实例化赌博机:
class Bandit:def __init__(self, arms=10):self.rates = np.random.rand(arms)def play(self, arm):rate = self.rates[arm]if rate > np.random.rand():return 1else:return 0bandit = Bandit()
Qs = np.zaro(10)
ns = np.zeros(10)Agent:
class Agent:def __init__(self, epsilon, action_size=10):self.epsilon = epsilonself.Qs = np.zeros(action_size)self.ns = np.zeros(action_size)def update(self, action, reward):self.ns[action] += 1self.Qs[action] += (reward - self.Qs[action]) / self.ns[action]def get_action(self):if np.random.rand() < self.epsilon:return np.random.randint(0, len(self.Qs))return np.argmax(self.Qs)完整代码:
import numpy as np
import matplotlib.pyplot as pltclass Bandit:def __init__(self, arms=10):self.rates = np.random.rand(arms)def play(self, arm):rate = self.rates[arm]if rate > np.random.rand():return 1else:return 0class Agent:def __init__(self, epsilon, action_size=10):self.epsilon = epsilonself.Qs = np.zeros(action_size)self.ns = np.zeros(action_size)def update(self, action, reward):self.ns[action] += 1self.Qs[action] += (reward - self.Qs[action]) / self.ns[action]def get_action(self):if np.random.rand() < self.epsilon:return np.random.randint(0, len(self.Qs))return np.argmax(self.Qs)if __name__ == '__main__':steps = 1000epsilon = 0.1bandit = Bandit()agent = Agent(epsilon)total_reward = 0total_rewards = []rates = []for step in range(steps):action = agent.get_action() #选择行动reward = bandit.play(action) #玩家实际得到的报酬agent.update(action, reward) #从当前报酬和行动中学习total_reward += rewardtotal_rewards.append(total_reward)rates.append(total_reward / (step + 1))print(total_reward)plt.ylabel('Total reward')plt.xlabel('Steps')plt.plot(total_rewards)plt.show()plt.ylabel('Rates')plt.xlabel('Steps')plt.plot(rates)plt.show()结果:

结果是859,即执行1000回有859回中
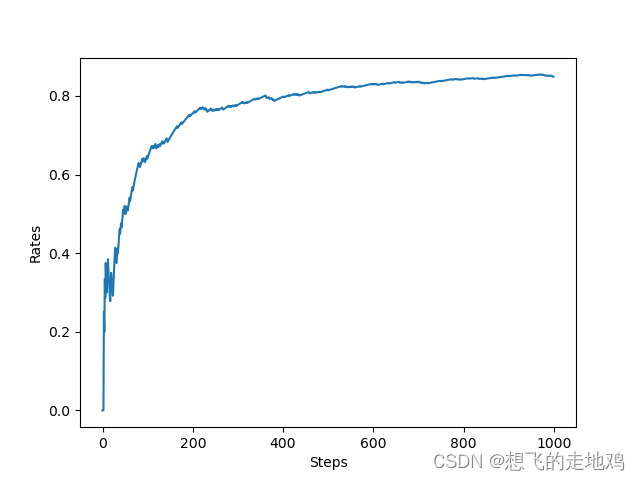
胜率在100step时时0.4,500step之后超过0.8.也就是说明agent已经能正确学习了。
这篇关于从零开始强化学习一:Bandit Problem的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








