ConvNets 与 Vision Transformers：数学深入探讨

        作为背景，在快速发展的深度学习领域，有两种架构在图像“分类”任务中脱颖而出：卷积神经网络（ConvNets）和视觉变换器（ViTs）。虽然从业者经常交替使用它们进行分类，但它们的数学基础是不同的。

        在本文中，我深入研究了这些架构的数学原理，阐明了它们在分类方面的功能等效性以及生成任务中的差异。我还提供了关于预算如何根据具体情况趋同或不同的数学比较。

二、深入探讨非生成功能等价

2.1. 层次特征空间

        卷积网络：

        给定输入I和滤波器 { Fk ​}，卷积定义为：

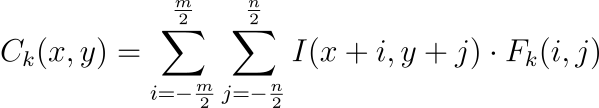
        堆叠这些卷积：

        其中σ是激活函数，bk​是偏置项。

        维特：

        代币进行自我关注：

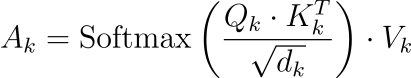
        整个序列演变为：

        两种架构都基于其输入逐层构建，对分层模式进行建模。

2.2. 注入非线性

        卷积网络：

        ReLU常用：

        维特：

        GELU 在变形金刚中很典型：

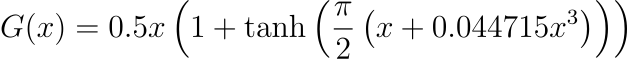
        这些非线性确保模型可以捕获复杂的模式。

2.3. 分类参数化的效率

        卷积网络：

        由于权重共享：

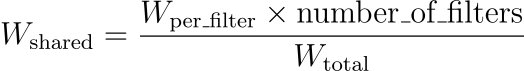
        维特：

        尽管它们随序列长度呈二次方增长，但像 Linformer 这样的线性近似：

        两者都描绘了特征空间，形成稳健的决策边界。

到目前为止，我们了解到，虽然 ConvNet 和 Vision Transformer 具有不同的数学基础，但它们在分类任务中表现出显着的功能等效性。他们捕获分层模式并对其进行有效分类的方法使它们成为从业者的首选。

三、非生成式培训预算：它们的协调点

        在非生成任务（主要是分类）中，两种架构的训练预算表现出显着的相似性。让我们从数学上探讨一下这个问题。

3.1. 计算复杂度

        卷积网络：

        卷积层的计算成本为：

        其中K是滤波器大小，M × N是特征图大小。

        维特：

        对于自我关注：

        其中L是序列长度，N是特征维度。

        在实践中，对于大规模数据集和深度网络，这些复杂性往往会收敛，特别是在使用 Linformer 或 Performer 等高效转换器变体时。

3.2. 内存占用

        卷积网络：

        由于权重共享，所需的内存为：

        其中D_in​ 和D_out​ 是输入和输出深度。

        维特：

        内存成本为：

        同样，通过有效的变体和优化，内存占用量可以与大规模分类任务紧密结合。

正如我们所看到的，从数学上来说，ConvNet 和 Vision Transformer 在大规模分类任务的非生成任务的训练预算方面是趋同的。

四、生成任务：分歧

4.1. 空间相干性

        卷积网络：

        它们本质上保持空间连贯性：

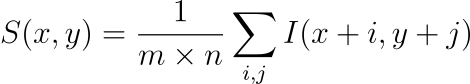
        维特：

        ViT 需要位置嵌入：

        虽然 ConvNet 生成自然平滑的图像，但 ViT 可能需要添加约束。

4.2. 顺序数据生成

        卷积网络：

        在 PixelCNN 等架构中：

        维特：

        Transformer 自然地处理序列：

        ViT 在自然生成序列方面具有优势，而 ConvNet 需要特定的设计。

4.3.潜在空间动力学

        卷积网络：

        在 VAE 结构中：

        维特：

        更丰富的潜在空间的潜力：

        ViT 可能由于其自注意力机制而捕获复杂的潜在空间，而 ConvNet 可能需要更复杂的设计。

正如我们所看到的，当冒险进入生成领域时，他们固有的偏见明显地表现出来。

五、生成预算情景：出现差异的地方

当谈到生成任务时，ConvNet 和 ViT 的训练预算开始出现显着差异。

5.1. 空间连贯性和连续性

        卷积网络：

        固有的空间结构确保了局部相干的输出。因此，获得高质量图像可能需要更少的训练迭代：

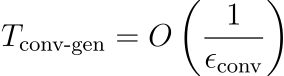
        其中ϵ_conv​是 ConvNet 的收敛速度。

        维特：

        ViT 缺乏固有的空间偏差，可能需要额外的训练迭代来确保生成图像的局部一致性：

        由于缺乏空间先验，ϵ_vit​通常小于ϵ_conv ​。

5.2. 潜在空间探索

        卷积网络：

        对 VAE 等生成模型中潜在空间的探索是直接的：

        其中Z是潜在空间的维数。

        维特：

        考虑到自注意力机制，ViT 可能会对潜在空间表现出更丰富的探索，但计算成本可能更高（这会在顺序依赖性中得到抵消）：

5.3. 顺序依赖

        卷积网络：

        尽管具有适应性，但卷积网络本质上并不是顺序的。因此，建模顺序依赖关系可能需要更复杂的设计和可能更长的训练（这是 ViT 在生成用例上击败 ConvNet 的地方）：

        其中τ是序列长度，δ_conv​是迭代因子。

        维特：

        鉴于 ViT 起源于 NLP，它可以自然地处理序列，从而有可能减少所需的训练迭代：

        其中δ_vit​通常小于δ_conv ​。

在生成场景中，情况发生了巨大的变化。具有空间先验的 ConvNet 可能在图像生成方面具有优势，而具有全局注意力的 ViT 可能更适合文本或多模态域生成等任务，且预算可能较少。同样，这在很大程度上取决于使用环境和数据集大小。背景很重要。

        希望这种数学深入研究能够提供一个视角来理解两种架构的优势和挑战，指导研究人员根据领域和上下文选择不同的任务。