本文主要是介绍统计学习笔记第 1 部分:Hoeffding 的不等式推导与模拟,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!

照片由Unsplash上的Luca Bravo拍摄
1:背景与动机
霍夫丁不等式是数理统计和机器学习 (ML) 中的一个重要的集中不等式,广泛应用于统计学习理论等理论领域以及强化学习等应用领域。
我注意到,在机器学习社区的一些地方,通常将 Hoeffding 的不等式呈现为“给定”,而对于所述不等式的来源仅提供轻微的直觉(如果有的话)。我通常不喜欢这种理解数学材料的“神奇思维”。鉴于我将在未来撰写的文章中广泛利用霍夫丁不等式,我将这篇文章作为从第一原理逐步推导出不等式的入门读物。
我们首先陈述霍夫丁不等式,并在接下来的部分中逐步清楚地推导该不等式。我们以计算模拟结束这篇文章,显示了这种不等式围绕随机变量和抽样估计量的经验估计提供的保守(但概率上正确)的界限。
假设我们有:

图片由作者提供
考虑到上述条件,霍夫丁不等式提供了以下双边统计不等式:
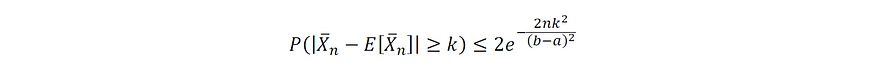
图片由作者提供
以下各节从第一原理推导出上述不等式。本文的目录如下:

图片由作者提供
话虽如此,让我们开始吧。
2:马尔可夫不等式
从第一原理开始,我们从马尔可夫不等式开始。
假设我们有:
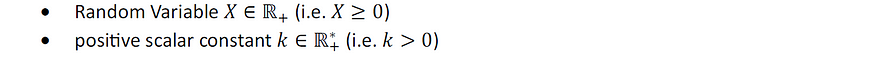
图片由作者提供
考虑到上述条件,马尔可夫不等式提供了以下统计不等式:
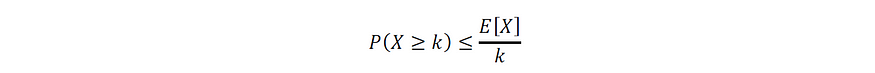
图片由作者提供
证明:
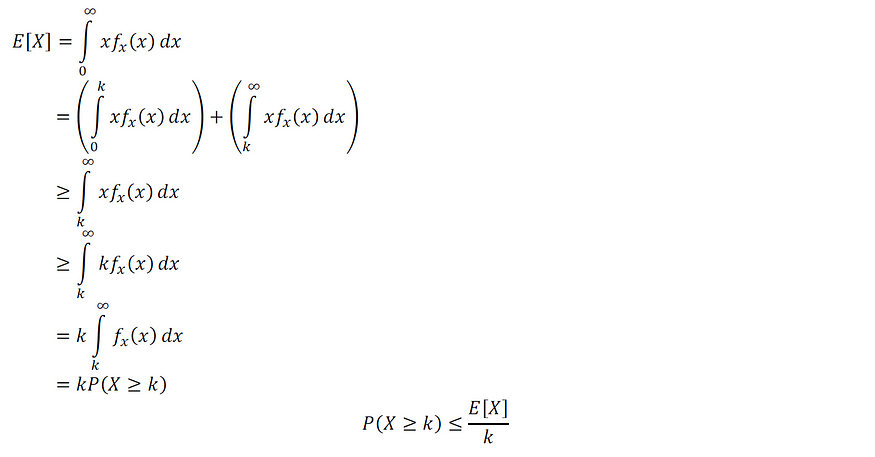
图片由作者提供
马尔可夫不等式提供了相当宽松的界限。如果我们感兴趣的随机变量具有定义的有限方差,我们可以用切比雪夫不等式收紧马尔可夫不等式,如下一节所示。
3:切比雪夫不等式
接下来我们讨论切比雪夫不等式,它是马尔可夫不等式的直接结果。
假设我们有:

图片由作者提供
考虑到上述条件,切比雪夫不等式提供了以下统计不等式:
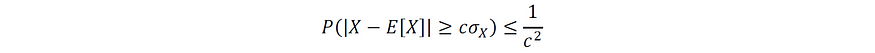
图片由作者提供
证明:
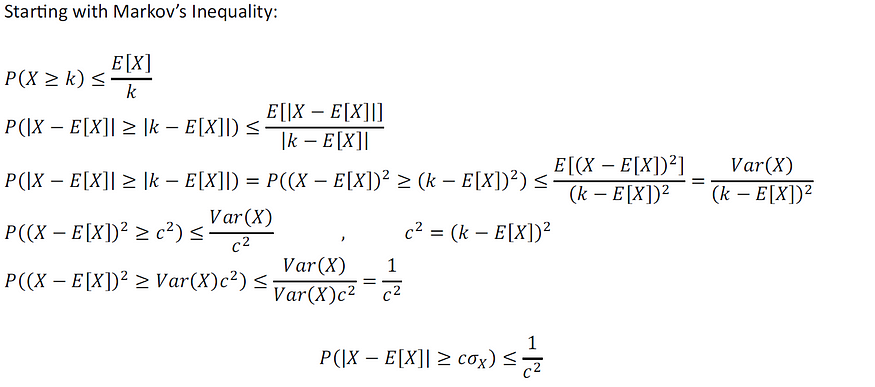
图片由作者提供
请注意,上面我们利用的X具有定义的且有限的方差,即它的二阶矩是定义的且有限的。如果X的定义矩达到r级, 我们可以将上面的公式扩展到以下不等式:
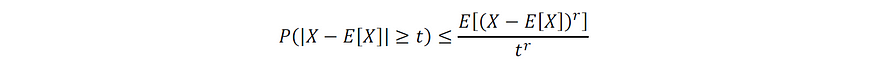
图片由作者提供
对于许多随机变量,矩生成函数(MGF)将存在于零附近的邻域中,即 MGF 对于所有 | 都是有限的。t |≤ b其中b>0是某个常数。在这些情况下,我们可以使用 MGF 生成尾部边界,就像下一节中的切尔诺夫边界的情况一样。
4:切尔诺夫界限
通过将切比雪夫不等式扩展到更高级别的矩,我们推导出切尔诺夫界。
假设我们有:
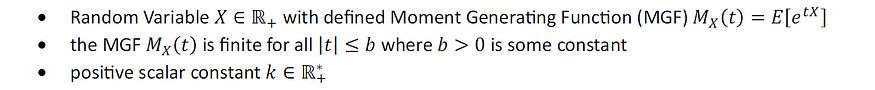
图片由作者提供
考虑到上述条件,切尔诺夫界限提供了以下统计不等式:
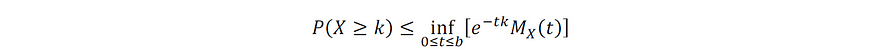
图片由作者提供
证明:
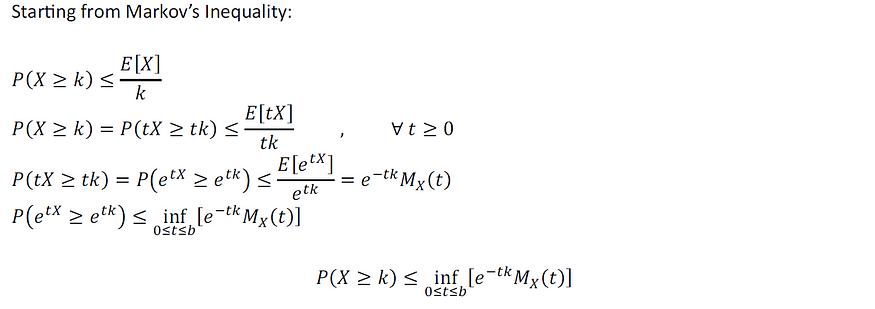
图片由作者提供
在第 6 节中,我们将专门针对高斯随机变量导出切尔诺夫界限。然而,为了准备这样做,我们将首先在下一节中导出高斯随机变量的 MGF。
5:高斯随机变量的矩生成函数(MGF)
我们将首先推导单个高斯随机变量的矩生成函数(MGF),然后推导独立同分布高斯随机变量的中心均值的 MGF。
5.1:单高斯随机变量的MGF
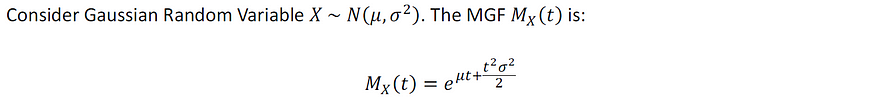
图片由作者提供
证明:

图片由作者提供
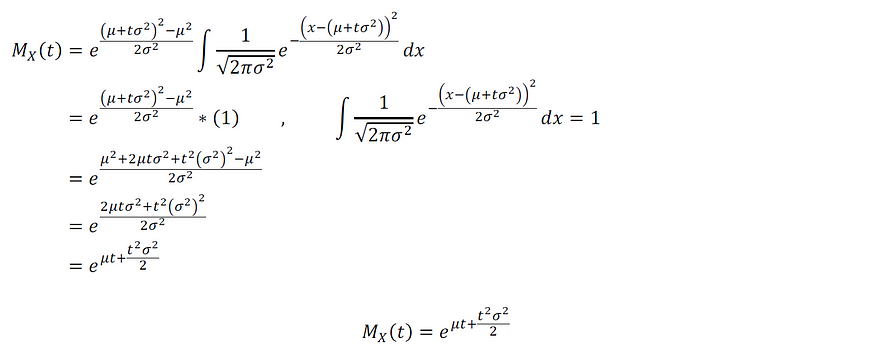
图片由作者提供
接下来,我们将上述扩展到独立同分布高斯随机变量的中心均值。
5.2:独立同分布高斯随机变量的中心均值 MGF
考虑n 个相同且独立分布 (iid) 的高斯随机变量:
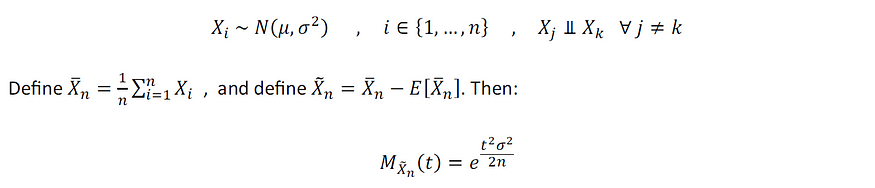
图片由作者提供
证明:
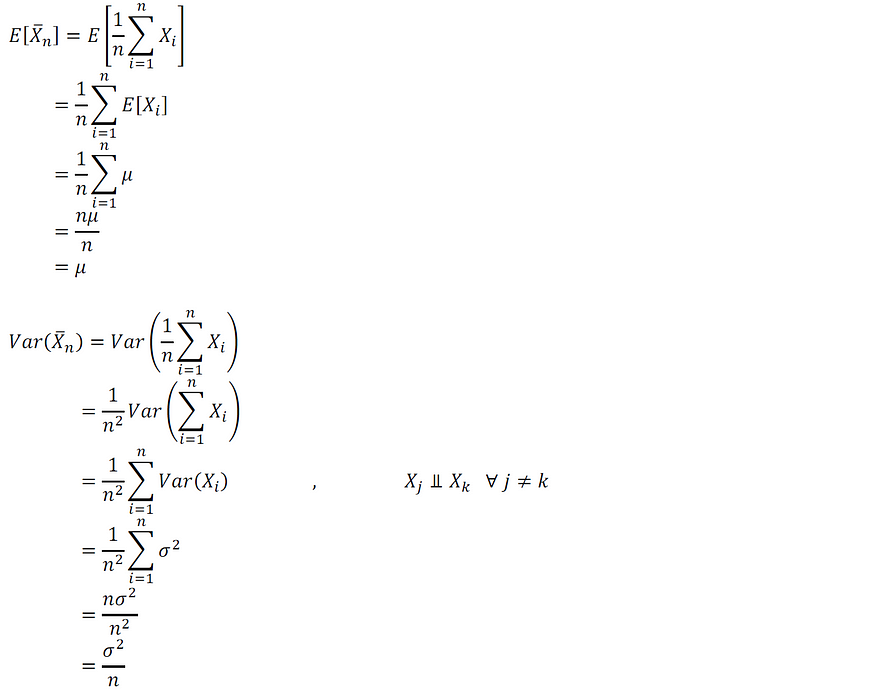
图片由作者提供
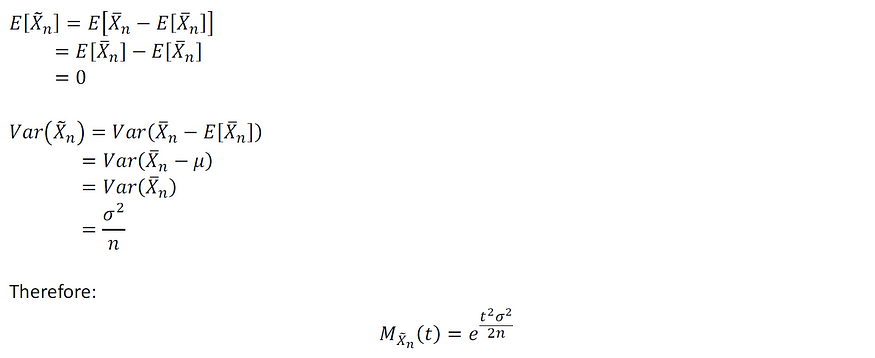
图片由作者提供
6:通过切尔诺夫边界的高斯尾边界
利用第 4 节和第 5 节中的信息,我们现在推导出独立同分布高斯随机变量的中心均值的切尔诺夫界限。

图片由作者提供
证明:

图片由作者提供

图片由作者提供
在下一节中,我们将探讨亚高斯随机变量,这是一组随机变量,我们可以从统计不平等的角度利用上面的高斯尾界。
7:亚高斯随机变量
在上一节中,我们导出了独立同分布高斯随机变量的中心均值的切尔诺夫界限。事实证明,这些高斯尾部不等式更广泛地适用于一类称为亚高斯随机变量的随机变量。粗略地说,这些随机变量的尾部衰减速度比高斯分布更快。
在下面的小节中,我们正式定义亚高斯随机变量的类,证明Rademacher随机变量在亚高斯类内,并证明所有有界随机变量都在亚高斯类内。
7.1:亚高斯随机变量类的定义

图片由作者提供

图片由作者提供
7.2:Rademacher 随机变量是亚高斯的
接下来我们证明 Rademacher 随机变量是亚高斯的。

图片由作者提供

图片由作者提供
7.3:所有有界随机变量都是亚高斯的
最后,我们将证明所有有界随机变量(即具有有界支持的变量)都是亚高斯的。
假设我们有:
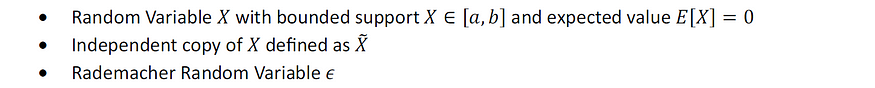
图片由作者提供

图片由作者提供
在下一节中,通过 Popoviciu 的方差不等式,我们表明方差不等式可以从(ba)²进一步收紧到(ba)²/4。
8:波波维丘的方差不等式
对于具有有界支持 [ a , b ] 的随机变量X,波波维丘不等式提供了方差 Var( X ) 上的以下不等式界:
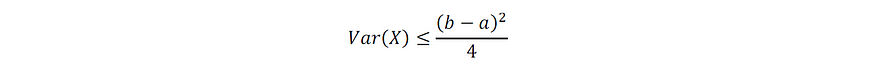
图片由作者提供
证明:

图片由作者提供
所以:
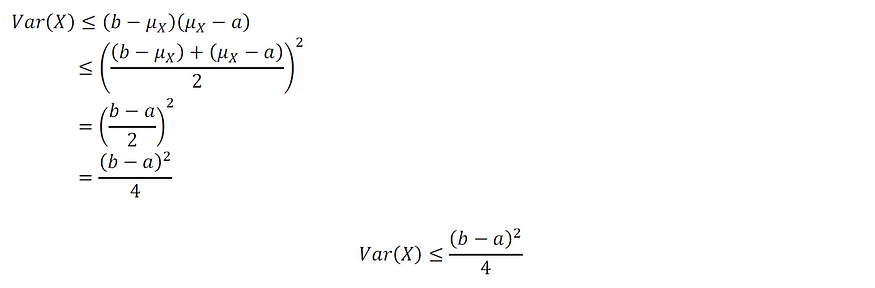
图片由作者提供
9:霍夫丁不等式
假设我们有:

图片由作者提供
采用第 7 节中的亚高斯尾界和第 8 节中的波波维丘不等式,我们有:
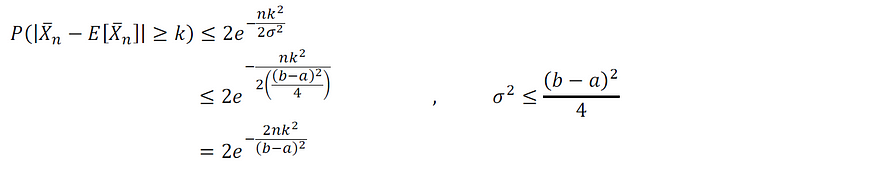
图片由作者提供
......我们最终得出两侧霍夫丁不等式:
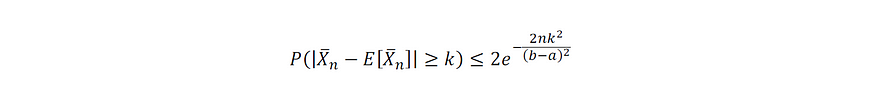
图片由作者提供

图片由作者提供
10:计算模拟
我们现在在 Python 中执行计算模拟,显示 Hoeffding 不等式可以围绕随机变量和抽样估计量的经验估计提供保守(但概率上正确)的界限。
让我们从加载我们的库开始:
,接下来创建一个函数来模拟数据并恢复 Hoeffding Bounds:
,最后恢复仿真结果:
根据上面的分析,我们模拟了 Rademacher、Beta、二项式、均匀和高斯采样估计器(亚高斯类内的所有参数分布)的数据,并恢复了 Hoeffding 界限(高斯采样估计器情况下的 Chernoff 界限):增量为 20%。从上面的结果可以看出,Hoeffding 边界是保守的,但都提供了超过 20% 的覆盖率。
11:总结
未来我们将撰写有关有限和无限参数函数类的强化学习和统计学习理论的文章,其中利用霍夫丁不等式将至关重要。
为了参考扎实的统计学习理论内容,我会推荐拉里·瓦瑟曼(卡内基梅隆大学统计和机器学习教授)的教科书“所有统计”和“所有非参数统计”,以及斯坦福大学教师的“统计学习要素” 。
这篇关于统计学习笔记第 1 部分:Hoeffding 的不等式推导与模拟的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




