本文主要是介绍SAP_MIR7预制发票控制余额不为0则不允许保存，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
MIR7预制发票时，右上角的自动计算余额不为0，则不允许保存
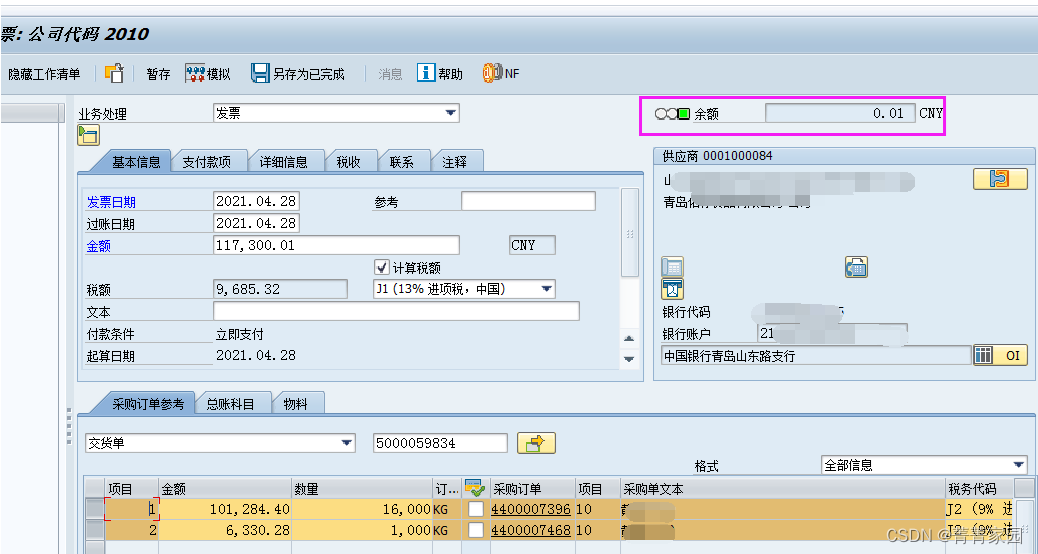
解决方案：
物料管理—后勤发票校验—发票冻结—设置容差限制
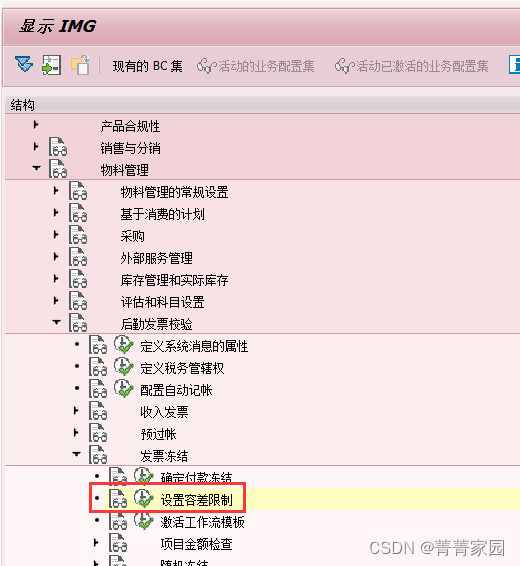
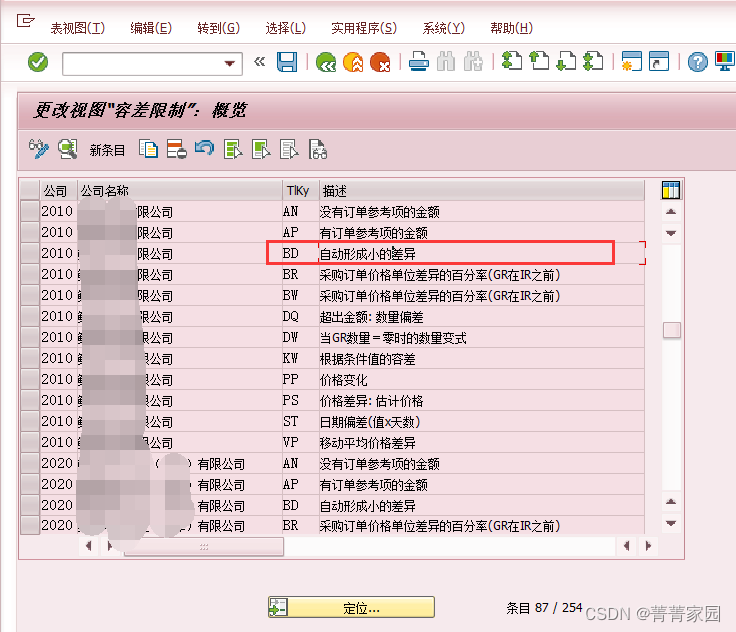
将BD自动形成小的差异，检查限制设置为空即可。
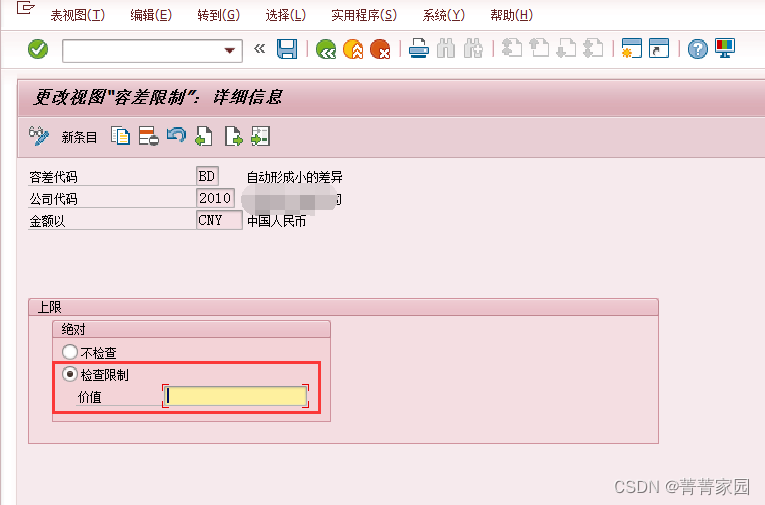
这篇关于SAP_MIR7预制发票控制余额不为0则不允许保存的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
相关文章
浅析如何使用Swagger生成带权限控制的API文档
《浅析如何使用Swagger生成带权限控制的API文档》当涉及到权限控制时,如何生成既安全又详细的API文档就成了一个关键问题,所以这篇文章小编就来和大家好好聊聊如何用Swagger来生成带有... 目录准备工作配置 Swagger权限控制给 API 加上权限注解查看文档注意事项在咱们的开发工作里，API
使用C++将处理后的信号保存为PNG和TIFF格式
《使用C++将处理后的信号保存为PNG和TIFF格式》在信号处理领域,我们常常需要将处理结果以图像的形式保存下来,方便后续分析和展示,C++提供了多种库来处理图像数据,本文将介绍如何使用stb_ima... 目录1. PNG格式保存使用stb_imagephp_write库1.1 安装和包含库1.2 代码解
Spring IOC控制反转的实现解析
《SpringIOC控制反转的实现解析》：本文主要介绍SpringIOC控制反转的实现,IOC是Spring的核心思想之一,它通过将对象的创建、依赖注入和生命周期管理交给容器来实现解耦,使开发者... 目录1. IOC的基本概念1.1 什么是IOC1.2 IOC与DI的关系2. IOC的设计目标3. IOC
vscode保存代码时自动eslint格式化图文教程
《vscode保存代码时自动eslint格式化图文教程》：本文主要介绍vscode保存代码时自动eslint格式化的相关资料,包括打开设置文件并复制特定内容,文中通过代码介绍的非常详细,需要的朋友... 目录1、点击设置2、选择远程--->点击右上角打开设置3、会弹出settings.json文件，将以下内
Python实现局域网远程控制电脑
《Python实现局域网远程控制电脑》这篇文章主要为大家详细介绍了如何利用Python编写一个工具,可以实现远程控制局域网电脑关机,重启,注销等功能,感兴趣的小伙伴可以参考一下... 目录1.简介2. 运行效果3. 1.0版本相关源码服务端server.py客户端client.py4. 2.0版本相关源码1
Spring Security 基于表达式的权限控制
前言 spring security 3.0已经可以使用spring el表达式来控制授权，允许在表达式中使用复杂的布尔逻辑来控制访问的权限。 常见的表达式 Spring Security可用表达式对象的基类是SecurityExpressionRoot。 表达式描述hasRole([role])用户拥有制定的角色时返回true （Spring security默认会带有ROLE_前缀）,去
豆包 MarsCode 不允许你还没有女朋友
在这个喧嚣的世界里，爱意需要被温柔地唤醒。为心爱的她制作每日一句小工具，就像是一场永不落幕的浪漫仪式，每天都在她的心田播撒爱的种子，让她的每一天都充满甜蜜与期待。 背景 在这个瞬息万变的时代，我们都在寻找那些能让我们慢下来，感受生活美好的瞬间。为了让这份浪漫持久而深刻，我们决定为女朋友定制一个每日一句小工具。这个工具会在她意想不到的时刻，为她呈现一句充满爱意的话语，让她的每一天都充满惊喜和感动
深入解析秒杀业务中的核心问题 —— 从并发控制到事务管理
深入解析秒杀业务中的核心问题 —— 从并发控制到事务管理 秒杀系统是应对高并发、高压力下的典型业务场景，涉及到并发控制、库存管理、事务管理等多个关键技术点。本文将深入剖析秒杀商品业务中常见的几个核心问题，包括 AOP 事务管理、同步锁机制、乐观锁、CAS 操作，以及用户限购策略。通过这些技术的结合，确保秒杀系统在高并发场景下的稳定性和一致性。 1. AOP 代理对象与事务管理 在秒杀商品
PostgreSQL中的多版本并发控制（MVCC）深入解析
引言 PostgreSQL作为一款强大的开源关系数据库管理系统，以其高性能、高可靠性和丰富的功能特性而广受欢迎。在并发控制方面，PostgreSQL采用了多版本并发控制（MVCC）机制，该机制为数据库提供了高效的数据访问和更新能力，同时保证了数据的一致性和隔离性。本文将深入解析PostgreSQL中的MVCC功能，探讨其工作原理、使用场景，并通过具体SQL示例来展示其在实际应用中的表现。 一、