本文主要是介绍强化学习中值的迭代,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
一、价值的迭代
策略迭代的一个缺点是,其每次迭代都涉及策略评估,这本身可能是一个漫长的迭代计算,需要多次遍历状态集。如果策略评估是迭代进行的,那么只有当趋近于vπ时才会收敛。我们是否必须等待完全收敛,还是可以在达到该点之前停止?网格世界的示例表明中断策略评估是可行的。在该示例中,超过前三个迭代步骤的策略评估对相应的贪婪策略没有影响。
事实上,策略迭代的策略评估步骤可以在不失去策略迭代收敛保证的情况下中断。一个重要的特殊情况是在仅进行一次遍历后停止策略评估(每个状态的一次备份)。这个算法称为值迭代。它可以写成一个特别简单的操作,该操作结合了策略改进和中断策略评估步骤:
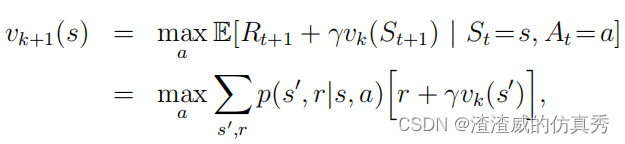
对于所有的s∈S。对于任意v0,{vk}序列在保证v∗存在的相同条件下可以证明收敛到v∗。
理解价值迭代另一种方式是通过参考贝尔曼最优方程。价值迭代是通过将贝尔曼最优方程转化为更新规则而获得的。另外,价值迭代备份与策略评估相同,除了需要取所有动作的最大值。另一种看到这种紧密关系的方法是比较这些算法的图。最后,考虑价值迭代如何终止。与策略评估一样,价值迭代需要正式进行无限次迭代才能精确收敛到v∗。在实践中,一旦价值函数在一个遍历中的变化量很小,我们就会停止。图1给出了具有这种终止条件的价值迭代完整算法。

图1
价值迭代有效地在其每次扫描中结合了政策评估的一次扫描和政策改进的一次扫描。通过在每次政策改进扫描之间插入多次政策评估扫描,通常可以更快地收敛。一般来说,截断策略迭代算法的整个类可以被认为是扫描序列,其中一些使用策略评估备份,另一些使用价值迭代备份。所以这仅仅意味着将最大操作添加到一些策略评估的扫描中。所有这些算法都会收敛到折扣有限MDP的最优策略。
二、典型示例
赌徒问题。一个赌徒有机会在掷硬币的结果上进行下注。如果硬币出现正面,他赢得与他在那次掷硬币中下注的赌注相同的美元数;如果是反面,他输掉了赌注。游戏在赌徒赢得100美元的目标或输光资金后结束。在每次掷硬币时,赌徒必须决定他的资本中下注多少,以整数的美元数。这个问题可以表述为一个非贴现的、独立的、有限的MDP(马尔可夫决策过程)。
状态是赌徒的资本,s ∈ {1, 2, . . . , 99},动作是赌注,a ∈ {0, 1, . . . , min(s, 100-s)}。奖励在所有转换上都是零,除了在赌徒达到他的目标时的奖励+1。然后状态值函数给出从每个状态获胜的概率。策略是从资本水平到赌注的映射。最优策略最大化达到目标的概率。如果ph(正面朝上的概率)是已知的,那么整个问题就是已知的,例如可以通过值迭代来解决。
图2显示了通过连续的价值迭代扫描,值函数的变化以及找到的最优策略,对于ph = 0.4的情况。这个策略是最优的,但不是唯一的。事实上,存在一整个最优策略族,它们都对应于最优值函数的argmax动作选择上的平局。对于ph = 0.4的赌徒问题的解决方案。图2显示了通过连续的价值迭代扫描找到的值函数。下图显示了最终策略。
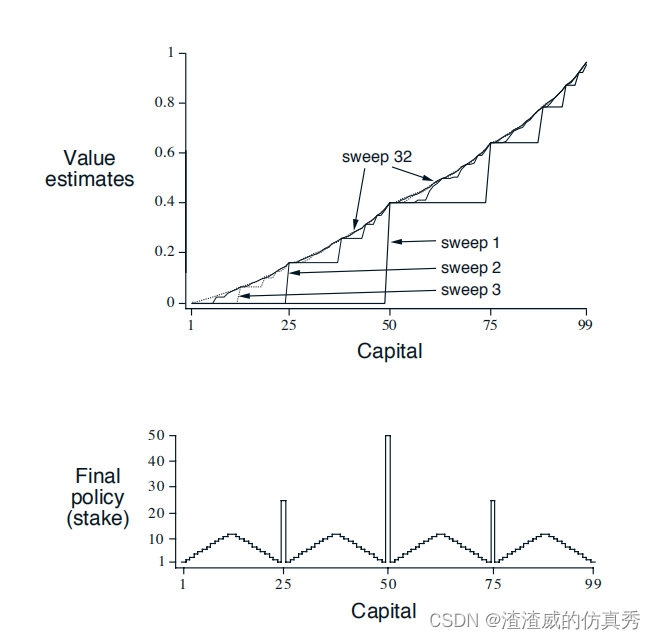
图2
这篇关于强化学习中值的迭代的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








