Trouble of Tyrant （固定图边加长最短路转直线群最小值）

本文主要是介绍Trouble of Tyrant （固定图边加长最短路转直线群最小值），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

题目来源

2018 ACM-ICPC 中国大学生程序设计竞赛线上赛

Tyrant has a private island on the Pacific Ocean. He has built many luxury villas on the island. He flies here every vacation to enjoy life. He will drive his sports car between his villas. Tyrant has n villas on the island and the last villa which is numbered by n is his favorite. His money is only allowed to build one airpor located at the first villa which is numbered by 1 so every time he come to the island, he will land at the villa numbered 1. What's more Tyrant build 2*n-3 roads on the island. For every villa except the first island, there is a two-way street connecting this villa and the first villa. For every villa numbered by i (i >= 3) there is a two-way street connecting this villa and the villa numbered by i - 1. Tyrant is not satisfied, he think the road is not long enough. He asks q problems, every problem has a non negative integer d. He want to know if the length of each road is increaced by d what is the shortest distance between the first villa and his favorite villa. Notice that the increment in each problem is not cumulative -- in other words it doesn't take effect on the real road after query.

Input:

The first integer indicate the number of test cases T (T <= 10).

In each test cases the first line contains two integers n and q -- the number of villas and the number of queries (3 <= n <= 100000, 1 <= q <= 100000).

The second line contains n - 1 non-negative integers -- ai describe a road with length ai connecting villa 1 and i (2 <= i <= n)

The third line contains n - 2 non-negative integers -- bi describe a road with length bi connecting villa i - 1 and i (3 <= i <= n)

The next line contains q non-negative integers -- di means Tyrant want to know what is the shortest distance between the first villa ans his favorite villa when the length of each road is increaced by di.

All integers are 32-bit signed integer.

Output:

For each test case you should output q integers in one line means the answer for each problem.

样例输入

样例输出

3 7 9

【题意】

一个无向图，n个点，从1至n都有一条边，从3~n每一个点都与前一个点有条边。

然后q次询问，每次输入一个d，问假如把图的每条边都增加d，那么从1->n的最短路是多少

【分析】

这是昨天宁夏网络赛的一道题，当时二分查找没处理好就是不对，今天二分查找后面加了句l--，踢掉了原来那句，奇迹般的过了。

通过画图很容易发现从1->n的路径只有两条，要么直达，要么先一步去2~n-1中的一个，再往后一步步走到n。

那么就可以算一算，对于每一个点i，1->i ->n的初始路长是多少（这是一个定值），存在数组c[]中

当询问时，对于每个点的路长为 c[i] + (n-i+1)*d ，那么就需要求出可以作为最小值得i，即某个点满足这个式子是最小值。

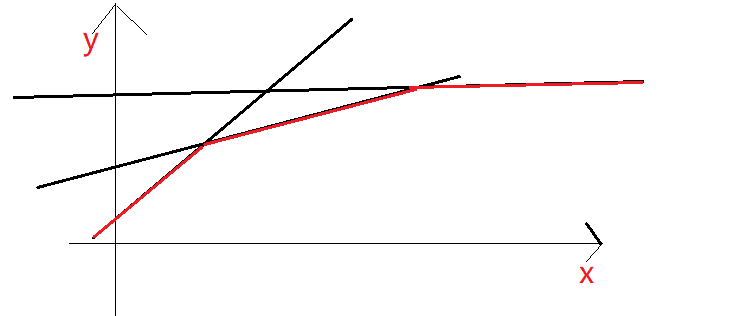
令斜率a=n-i+1，截距b=c[i]，令自由变量x=d，就会发现这是一个一元一次直线，而把每一个点i对应的那条直线，都画出来，大概是这样：

直线群相交形成的下边沿，就只能取到最小值的地方，对于不同的d，取最小值的直线不同，即图上的点不同。

接下来就要就出这个边沿，对于不同的d，选直线就行了。方法与bzoj 1007一样，题解。

将直线按斜率大小排序，斜率相同的按b小大排序，然后开始扫描，保存下能在下方的直线及其与前一直线的交点，便于二分找到d所在的位置。

【代码】

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=2e5+5;
const int INF=0x3f3f3f3f;
struct node {ll x,y;
}e[N];
ll a[N],b[N],c[N];struct line{//存直线ll a,b;double x1;int dex;
}l[502020],s[502020];//l存直线，s模拟栈
bool cmp(line l1,line l2)//按斜率
{if(l1.a==l2.a)return l1.b<l2.b;return l1.a>l2.a;
}
double getx(line l1,line l2)//求两直线交点的x坐标
{return 1.0*(l2.b-l1.b)/(l1.a-l2.a);
}
int main()
{int T,n,m,u,v,q,d;cin>>T;while(T--){scanf("%d%d",&n,&m);for(int i=2;i<=n;i++) scanf("%d",&a[i]);for(int i=3;i<=n;i++) scanf("%d",&b[i]);c[n]=0;for(int i=n-1;i>=2;i--) c[i]=c[i+1]+b[i+1];for(int i=2;i<=n;i++) c[i]+=a[i];for(int i=2;i<=n;i++)l[i]=line{n-i+1,c[i]}; //step, lensort(l+2,l+n+1,cmp);int top=0;//s的下标s[++top]=l[2];s[top].x1=0;s[top].dex=2;for(int i=3;i<=n;i++)//遍历直线{if(l[i].a==l[i-1].a)continue;//会被覆盖while(top>1&&getx(l[i],s[top])<getx(s[top],s[top-1]))top--;//可以覆盖上一条直线s[++top]=l[i];s[top].x1=getx(s[top],s[top-1]);s[top].dex=i;}for(int i=0;i<m;i++){scanf("%d",&d);int l=1,r=top+1,mid;while(l<r){mid=(l+r)/2;if(s[mid].x1>d)r=mid;else l=mid+1;}l--;int dex=s[l].dex;ll ans=c[dex]+1ll*(n-dex+1)*d;if(i)printf(" ");printf("%lld",ans);}printf("\n");}
}

这篇关于Trouble of Tyrant （固定图边加长最短路转直线群最小值）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！