轮廓线dp：GYM103446C

2023-11-06 16:44

文章标签 dp 轮廓线 gym103446c

本文主要是介绍轮廓线dp：GYM103446C，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

https://vjudge.net/contest/591700#problem/H

考虑轮廓线dp，当我们枚举到蓝色格子的时候，我们记录红色格子的状态

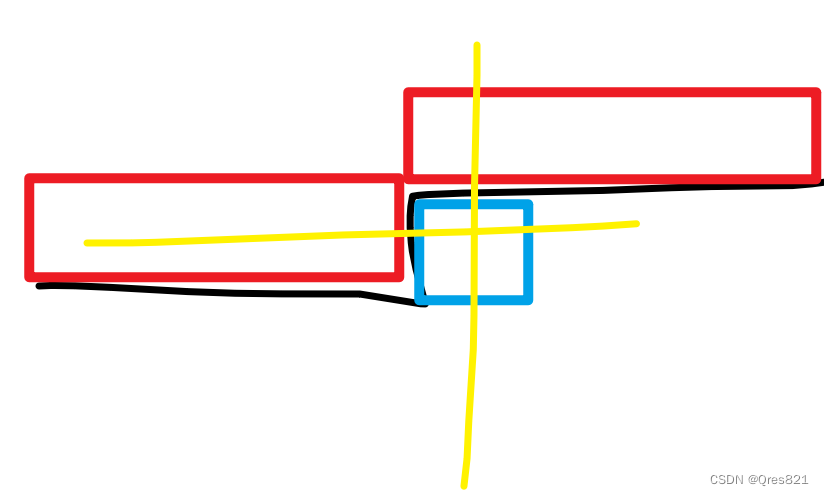
在这里插入图片描述

每个格子有4种状态

0有向下
1需要向上
2不用管
3需向右

每次枚举的时候，我们需要考虑这个格子的三种状态：

1
0+不放
0+放

他们会对所有3和同列的值造成影响

当枚举到行末时，我们需要“换行”，把所有3变成1

发现枚举过程中还有再维护一个0/1状态d，表示此行有没有向左

分类讨论即可

$O(2nm4^m)$

#include<bits/stdc++.h>
using namespace std;
#ifdef LOCAL#define debug(...) fprintf(stdout, ##__VA_ARGS__)
#else#define debug(...) void(0)
#endif
//#define int long long
inline int read(){int x=0,f=1;char ch=getchar(); while(ch<'0'||
ch>'9'){if(ch=='-')f=-1;ch=getchar();}while(ch>='0'&&ch<='9'){
x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}return x*f;}
#define Z(x) (x)*(x)
#define pb push_back
#define fi first
#define se second
//srand(time(0));
#define N 11
#define M 100000
//#define mo
void Min(int &a, int b) {a=min(a, b); 
}
int n, m, i, j, k, T;
int f[N][N][M][2], s, t, d, ans, c, a[N][N]; 
char str[N]; namespace Num {int omg, pw[N], b[N]; int Chan1[M], Chan2[M], Find1[M], Get[M][N], becom[M][N][4]; int zh(int *a) {int ans=0, i; for(i=1; i<=m; ++i) ans=ans*4+a[i]; return ans; }void chai(int s, int *a) {int i; for(i=m; i>=1; --i) a[i]=s%4, s/=4; }void Pre_num() {for(i=1, omg=1, pw[0]=1; i<=m; ++i) omg*=4, pw[i]=pw[i-1]*4; for(i=1; i<=m; ++i) b[i]=2; f[1][0][zh(b)][0]=0; for(s=0; s<omg; ++s) {chai(s, b); //all 3 -> 1for(i=1; i<=m; ++i) if(b[i]==3) b[i]=1; Chan1[s]=zh(b); chai(s, b); //all 3 -> 3for(i=1; i<=m; ++i) if(b[i]==3) b[i]=2; Chan2[s]=zh(b); chai(s, b); //find s[i]for(i=1; i<=m; ++i) Get[s][i]=b[i]; for(i=1; i<=m; ++i) if(b[i]==1) break; if(i<=m) Find1[s]=1; //if s has 1for(i=1; i<=m; ++i) {chai(s, b); for(k=0; k<4; ++k) {b[i]=k; becom[s][i][k]=zh(b); //make s[i] to k}}}}int Change(int s, int i, int x) {return becom[s][i][x]; }
};signed main()
{#ifdef LOCALfreopen("in.txt", "r", stdin);freopen("out.txt", "w", stdout);#endif
//	T=read();
//	while(T--) {
//
//	}memset(f, 0x3f, sizeof(f)); n=read(); m=read(); for(i=1; i<=n; ++i) {scanf("%s", str+1); for(j=1; j<=m; ++j) a[i][j]=str[j]-'0'; }Num::Pre_num(); for(i=1; i<=n; ++i) {for(j=1; j<=m; ++j) {for(s=0; s<Num::omg; ++s) for(d=0; d<=1; ++d) {if(f[i][j-1][s][d]>=100) continue; debug("[%d %d] %d %d\n", i, j-1, s, d); c=Num::Get[s][j]; if(a[i][j]==0 || a[i][j]==2) {t=s; if(c==2 && d==0) t=Num::Change(t, j, 3); Min(f[i][j][t][d], f[i][j-1][s][d]); /********************************/t=Num::Chan2[s]; t=Num::Change(t, j, 0); Min(f[i][j][t][1], f[i][j-1][s][d]+1); }if(a[i][j]==1 || a[i][j]==2) {if(c==1) continue; t=Num::Chan1[s]; 					if(c==0 || c==2) t=Num::Change(t, j, 2); Min(f[i][j][t][0], f[i][j-1][s][d]);}}}for(s=0; s<Num::omg; ++s) for(d=0; d<=1; ++d) {if(f[i][m][s][d]>=100) continue; t=Num::Chan1[s]; Min(f[i+1][0][t][0], f[i][m][s][d]); }}ans=1e9; for(s=0; s<Num::omg; ++s) if(Num::Find1[s]==0) Min(ans, f[n+1][0][s][0]); printf("%d", ans); return 0;
}