本文主要是介绍《误差理论》——粗大误差,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
粗大误差
超出在规定条件下预期的误差
1、粗大误差产生的原因
- 测量人员的主观原因
- 外界条件的客观原因
2、判别粗大误差的准则
(1)3 σ \sigma σ准则(莱以特准则)
∣ v i ∣ > 3 σ |v_i|>3\sigma ∣vi∣>3σ,则认为它含有粗大误差,应予剔除
(2)罗曼诺夫斯基准则(t检验准则)
设对某量作多次等精度独立测量,得 x 1 , x 2 , . . . , x n x_1,x_2,...,x_n x1,x2,...,xn认为 x j x_j xj为可疑数据,将其剔除后计算平均值为 x ˉ = 1 n ∑ i = 1 , i ≠ j x i \bar{x}=\frac{1}{n}\sum_{i=1,i\ne{j}}x_i xˉ=n1i=1,i=j∑xi并求得测量列的标准差(不包括 v j = x j − x ˉ v_j=x_j-\bar{x} vj=xj−xˉ σ = ∑ i = 1 n v i 2 n − 2 \sigma=\sqrt{\frac{\sum_{i=1}^{n}v_i^2}{n-2}} σ=n−2∑i=1nvi2查t分布的检验系数 K ( n , α ) K(n,\alpha ) K(n,α),若 ∣ x j − x ˉ ∣ > K σ |x_j-\bar{x}|>K\sigma ∣xj−xˉ∣>Kσ则认为 x j x_j xj为粗大误差,剔除
(3)格罗布斯准则(数据应服从正态分布)
x 1 , x 2 , . . . , x n x_1,x_2,...,x_n x1,x2,...,xn x i x_i xi服从正态分布,将 x i x_i xi从小到大顺序排列 x ( 1 ) ≤ x ( 2 ) ≤ . . . ≤ x ( n ) x_{(1)}\le x_{(2)}\le ...\le x_{(n)} x(1)≤x(2)≤...≤x(n)若认为 x ( 1 ) x_{(1)} x(1)可疑,则有 g ( 1 ) = x ˉ − x ( 1 ) σ g_{(1)}=\frac{\bar{x}-x_{(1)}}{\sigma} g(1)=σxˉ−x(1)若认为 x ( n ) x_{(n)} x(n)可疑,则有 g ( 1 ) = x ( 1 ) − x ˉ σ g_{(1)}=\frac{x_{(1)}-\bar{x}}{\sigma} g(1)=σx(1)−xˉ当 g ( i ) ≥ g 0 ( n , α ) g_{(i)}\ge g_0(n,\alpha ) g(i)≥g0(n,α)(查表得)即判别该测得值含有粗大误差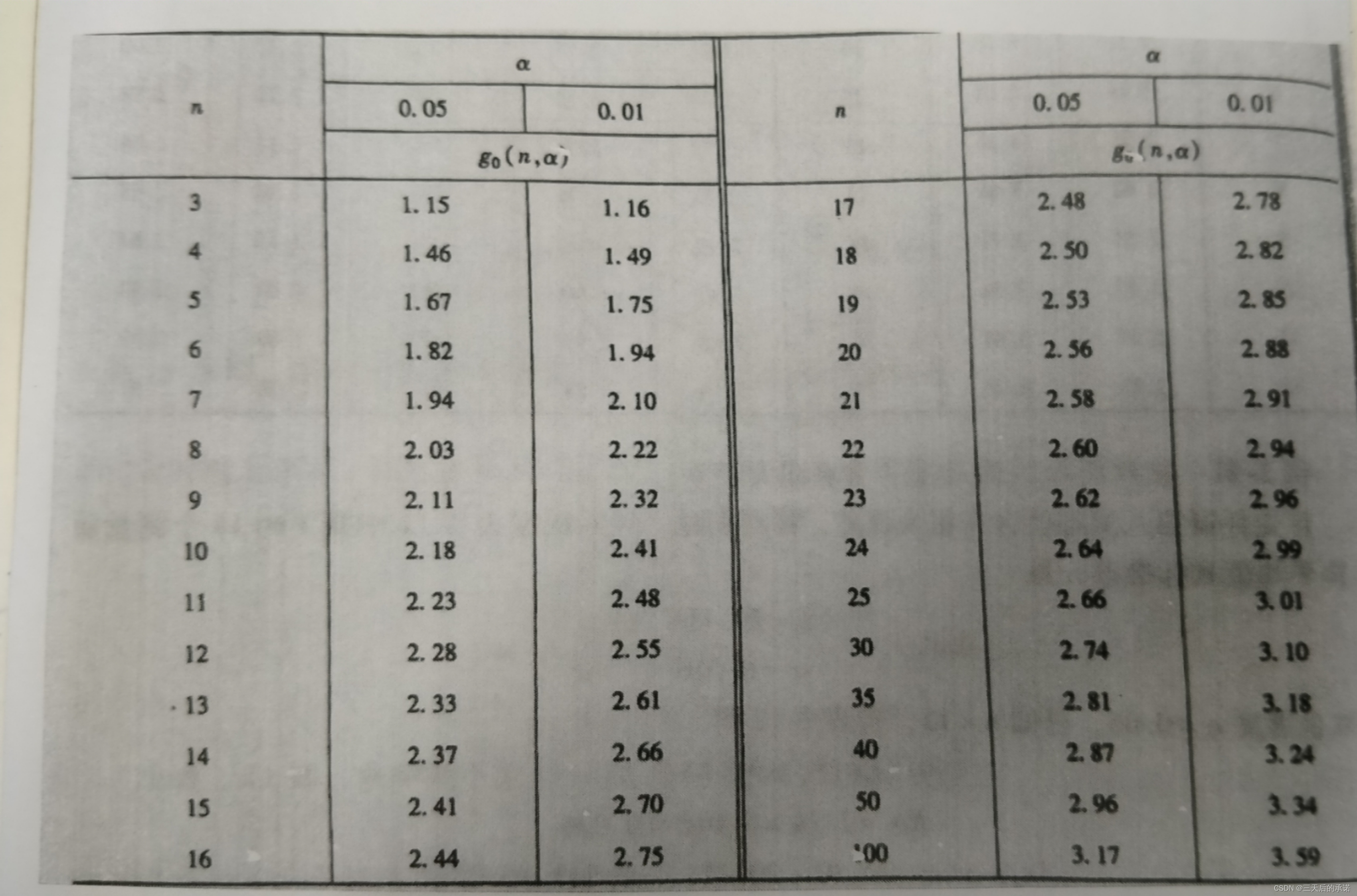
(4)狄克松准则
x 1 , x 2 , . . . , x n (小 − − > 大) x_1,x_2,...,x_n(小-->大) x1,x2,...,xn(小−−>大) x i x_i xi服从正态分布,统计量为 最大值 { r 10 = x n − x n − 1 x n − x 1 r 11 = x n − x n − 1 x n − x 2 r 21 = x n − x n − 2 x n − x 2 r 22 = x n − x n − 2 x n − x 3 最大值\left\{ \begin{array}{lr} r_{10}=\frac{x_n-x_{n-1}}{x_n-x_1}& \\ r_{11}=\frac{x_n-x_{n-1}}{x_n-x_2}& \\ r_{21}=\frac{x_n-x_{n-2}}{x_n-x_2}& \\ r_{22}=\frac{x_n-x_{n-2}}{x_n-x_3}& \end{array} \right. 最大值⎩ ⎨ ⎧r10=xn−x1xn−xn−1r11=xn−x2xn−xn−1r21=xn−x2xn−xn−2r22=xn−x3xn−xn−2 最小值 { r 10 = x 1 − x 2 x 1 − x n r 11 = x 1 − x 2 x 1 − x n − 1 r 21 = x 1 − x 3 x 1 − x n − 1 r 22 = x 1 − x 3 x 1 − x n − 2 最小值\left\{ \begin{array}{lr} r_{10}=\frac{x_1-x_2}{x_1-x_n}& \\ r_{11}=\frac{x_1-x_2}{x_1-x_{n-1}}& \\ r_{21}=\frac{x_1-x_3}{x_1-x_{n-1}}& \\ r_{22}=\frac{x_1-x_3}{x_1-x_{n-2}}& \end{array} \right. 最小值⎩ ⎨ ⎧r10=x1−xnx1−x2r11=x1−xn−1x1−x2r21=x1−xn−1x1−x3r22=x1−xn−2x1−x3选定显著度 α \alpha α,查表得 r 0 ( n , α ) r_0(n,\alpha ) r0(n,α)(查表得),若 r i j > r 0 ( n , α ) r_{ij}>r_0(n,\alpha ) rij>r0(n,α),则认为 x n x_n xn或 x 1 x_1 x1为粗大误差
效果好 { n ≤ 7 , r 10 8 ≤ n ≤ 10 , r 11 11 ≤ n ≤ 13 , r 21 n ≥ 14 , r 22 效果好\left\{ \begin{array}{lr} n\le7,\ r_{10}& \\ 8\le n\le10,\ r_{11}& \\ 11\le n\le13,\ r_{21}& \\ n\ge14,\ r_{22}& \end{array} \right. 效果好⎩ ⎨ ⎧n≤7, r108≤n≤10, r1111≤n≤13, r21n≥14, r22
这篇关于《误差理论》——粗大误差的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!









