复习交换代数——Noether正规化

本文主要是介绍复习交换代数——Noether正规化，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

简介
初等启发
证明过程
几何意义
定理应用
参考资料

简介

在交换代数中有如下定理

Noether正规化引理 令$R$是一个有限生成$k$-代数整环，则存在$t_1,\ldots,t_n\in R$使得$$k\subseteq_{\textrm{纯超越}} k[t_1,\ldots,t_n]\subseteq_{\textrm{整}} R$$其中纯超越指的是$t_1,\ldots,t_n$代数无关，整指的是任何$x\in R$都满足一个$k[t_1,\ldots,t_n]$上的整性方程。

该定理还有如下『加强包』

Noether正规化引理加强包1 如果$R=k[x_1,\ldots,x_n]$，且$k$是无限域，那么$t_i$可以选作其线性组合。

Noether正规化引理加强包2 如果预先选定真理想升链$\mathfrak{a}_1\subseteq \ldots \subseteq \mathfrak{a}_r$，那么还可以假设$$\mathfrak{a}_i\cap k[t_1,\ldots,t_n]=\left<t_1,\ldots,t_{h_i}\right>\qquad h_i\geq 0$$

以上两个『加强包』不冲突。

初等启发

首先，我们考虑一个初等的问题。

问题考虑单位圆$C: x^2+y^2=1$，如果多项式$f(x,y)$满足任何$C$上的点$(x,y)$都有$f(x,y)=0$，那么一定有$x^2+y^2-1| f(x,y)$。

简证这个问题当然非常简单，只需用$x^2+y^2-1$对$f(x,y)$作带余除法，得到的余式$r(x,y)$是关于$x$的一次式，这样，带入$y=0$，注意到$r(x,0)$有两个零点$x=\pm 1$于是$r(x,y)=0$。

或许你的高中老师强调过，所谓『曲线方程』，指的是『曲线上的点都满足方程，满足方程的点都在曲线上』。然而实际上曲线并不能完全决定方程，因为$(x^2+y^2-1)^2=0$也是上述单位圆的方程。而上面这个过程说明$x^2+y^2-1$是『最简的』。我们会作如下猜想

猜想是否对$n$元不可约多项式$f$定义的超曲面$C=\{f=0\}$，任意多项式$g$满足任何$C$上的点$p$带入都有$g(p)=0$，那么一定有$f | g$。

回顾上述过程，有两点原因迫使我们的证明失效。

例如$f(x)=x^2+1$，这是一个在实数上没有解的曲面，不可能指望任何多项式都被$x^2+1$整除。
例如$f(x,y)=xy-1$，此时我们不能使用带余除法，因为$x$前系数不是一个数。

为了规避第一点，我们只需要将$\mathbb{R}$换成某个代数闭域。为了规避第二点，我们相信经过某种变换，任何一个这样的多项式都可以变成关于$x$的最高次系数是一个数。例如这里，我们只需要带入$y=x+z$，即可得到$xy-1=x(x+z)-1=x^2+zx-1$。当然，直接变成双曲线也未尝不可。这一过程我们可以抽象成下面的定理。

定理(Noether) 对于域$k$上的多项式$f(X_1,\ldots,X_n)$，假如$k$是无限域，一定存在多项式$t_2,\ldots,t_n$使得$$f=\lambda X_1^n +\sum_{k<n} g_k(t_2,\ldots,t_n) X^k \qquad n\geq 0, \lambda\in k\setminus \{0\}, g_k\in k[t_2,\ldots,t_n]$$

证明对于$i\geq 2$，取$t_i=X_i+\lambda_i X_1$，带入$f$会发现只要保证$X_1$的最高次幂的系数不会被消成$0$即可，这总可以取恰当的$\lambda_i$避免。$\square$

证明中无限域用在了取$\lambda_i$上。当然，这件事Nagata做得更绝一些，他去掉了$k$无限的假设。

定理(Nagata) 对于域$k$上的多项式$f(X_1,\ldots,X_n)$，一定存在多项式$t_2,\ldots,t_n$使得$$f=\lambda X_1^n +\sum_{k<n} g_k(t_2,\ldots,t_n) X^k \qquad n\geq 0, \lambda\in k\setminus \{0\}, g_k\in k[t_2,\ldots,t_n]$$

证明对于$i\geq 2$，取$t_i=X_i+ X_1^{\lambda_i}$，带入$f$会发现$X_1$的次数空前的大，为了避免相消甚至可以取充分大的$\lambda_i$各展开出现的$\lambda X_i^k$两两次数不同。具体细节交给读者。$\square$

证明过程

下面是Noether正规化的证明。

Noether正规化的证明 证明分为几步.

约化到多项式环的情况 假设$R=k[x_1,\ldots,x_n]$, 考虑$k[X_1,\ldots,X_n]$到$R$自然映射$\varphi$, 考虑理想链$\ker\varphi\subseteq \varphi^{-1}(\mathfrak{a}_1)\subseteq \ldots \subseteq \varphi^{-1}(\mathfrak{a}_r)$. 不难验证如果多项式的情况得证了, 那么不难得到$R$的情况也正确. 最后验证时注意, $$\left<t_1,\ldots,t_{h_i}\right>=\varphi(\left<T_1,\ldots,T_{H_i}\right>)=\varphi(\varphi^{-1}(\mathfrak{a}_i)\cap k[T_1,\ldots, T_N]) =\mathfrak{a}_i \cap k[t_1,\ldots,t_n]$$最后的等号是由于$\ker \varphi\subseteq \varphi^{-1}(\mathfrak{a}_i)$
下面施加以归纳法, 在$r=1$, $\mathfrak{a}_i$是主理想$t_1R$时. 因为是真理想有$t_1\notin k$, 根据假设$t_1$是超越的. 根据上面Noether和Nagata的定理可以写成$$t_1= aX_1^{p}+\sum_{i<p}f_{i}X_1^{i}\quad a\in k, p\geq 0, f_{i}\in k[t_2,\ldots,t_n]$$上述整关系说明$X_1$在$k[t_1,\ldots,t_n]$上整, 注意到根据$t_i$的取法, $k[t_1,\ldots,t_n][X_1]=k[X_1,\ldots ,X_n]$, 从而$k[X_1,\ldots ,X_n]$在$k[t_1,\ldots,t_n]$上有整. 关于超越的论断则是超越基的一般推论. 而注意到$\mathfrak{a}_1\cap k[t_1,\ldots,t_n]\supseteq \left<t_1\right>$. 为了证明反面, 任意取左边的元素$x=t_1x'$, 则$x'=x/t_1\in k(t_1,\ldots ,t_n)\cap R$, 因为$k[t_1,\ldots,t_n]$是整闭的, 从而$x'\in k[t_1,\ldots,t_n]$, 从而$x\in \left<t_1\right>$.

接着处理一个理想的情形. 在$r=1$, 我们此时对$n$归纳, $n=1$时$k[X_1]$是主理想整环, 根据上一段是正确的. 对于$n\geq 2$, 任意选择主理想$t_1R\subseteq \mathfrak{a}_1$, 那么存在$t_1,u_2,\ldots ,u_n$满足条件. 那么用归纳假设, 在$k[u_2,\ldots ,u_n]$上考虑$\mathfrak{a}_1\cap k[u_2,\ldots ,u_n]$的情形. 最后验证时注意, 设$$x\in \sum f_i t_1^i\in \mathfrak{a}_1\cap k[t_1,\ldots,t_n]\quad f_i\in k[t_2,\ldots ,t_n]$$则$f_0=x-t_1(\ldots )\in \mathfrak{a}_1$, 从而$f_0\in \left<t_2,\ldots ,t_{h}\right>$, 从而$x\in \left<t_1,\ldots ,t_{h}\right>$.

最后处理一般情形. 对于$r\geq 2$, 利用归纳假设, 已经可以取到$t_1,\ldots,t_n$使得$$\mathfrak{a}_i\cap k[t_1,\ldots,t_n]=\left<t_1,\ldots,t_{h_i}\right>\quad \textrm{对某个正整数$h_i$, $1\leq i\leq r-1$}$$用上一段考虑$k[t_{h_{r-1}+1},\ldots,t_n]$与$\mathfrak{a}_r\cap k[t_{h_{r-1}+1},\ldots,t_n]$. 最后验证时注意, 假如记$h=h_i$, 那么$$x=\sum f_{(j)}t_{1}^{j_1}\ldots t_{h}^{j_{h}}\in \mathfrak{a}_i\cap k[t_1,\ldots,t_n]\quad f_{(j)}\in k[t_{h+1},\ldots ,t_n]$$则$f_{(0)}=x-t_1(\ldots )-\ldots -t_{h}(\ldots )\in \mathfrak{a}_i$从而$f_{(0)}\in \mathfrak{a}_i\cap k[t_{h+1},\ldots ,t_n]$. 而$$\mathfrak{a}_i\cap k[t_{h+1},\ldots ,t_n]=\begin{cases}\{0\}& 1\leq i\leq r-1\\ \left<t_{h+1},\ldots,t_{h_r}\right> & i=r\end{cases}$$

漫漫无期的归纳法终于结束. $\square$

上述证明虽然复杂，但是思路清晰，故过程有所简略，完整证明可见Altman & Kleiman A Term of Commutative Algebra。

几何意义

下面的讨论需要一些代数簇的几何。根据代数几何给出的代数和几何的对应

代数概念	几何概念
多项式环	仿射平面
整	有限
理想升链	代数集降链

就有Noether正规化的如下形态

Noether正规化引理 对于代数闭域$\Bbbk$，$\Bbbk$-代数簇$X$，则存在有限满射$X\to \mathbb{A}^n$，其中$n$是$X$的维数。

证明注意到满射的论断来自于对于整扩张$R_1\subseteq R_2$，则$\mathfrak{m}$是$R_2$的极大理想当且仅当$\mathfrak{m}\cap R_1$是$R_1$的极大理想，而上行定理确保满射。$n$是维数来自于Noether正规化的推论$\dim \mathcal{A}(X)=\operatorname{tr.deg}_{\Bbbk} \mathcal{K}(X)$，其中$\mathcal{A}$表示坐标环，$\mathcal{K}$表示有理函数域。$\square$

两个『加强包』也分别变成

Noether正规化引理加强包1 假设$X\subseteq \mathbb{A}^m$，存在一个$\mathbb{A}^m$的线性变换，将$X$映为$\mathbb{A}^n\subseteq \mathbb{A}^m$。

Noether正规化引理加强包2 假设$X_r\subseteq \ldots \subseteq X_0=X$是代数集，那么$X_i$可以被映成$\mathbb{A}^n$的线性子空间，或者用几何学家的术语，『切片（slide）』。

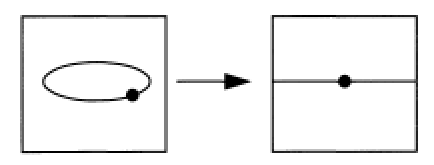
此图甚好，来自Eisenbud Commutative algebra GTM150。

定理应用

下面简单列举一下应用，主要就是零点定理了。

Schein零点定理 令$A$是交换环, 理想$\mathfrak{a}\subseteq R$, 那么$$\sqrt{a}=\bigcap_{\textrm{素理想}\mathfrak{p}\supseteq \mathfrak{a}}\mathfrak{p}$$

证明通过商去$\mathfrak{a}$, 可以假定$\mathfrak{a}=0$. 那么$$f\notin \sqrt{0}\iff 0\notin \{1,f,f^2,\ldots\}\iff A_f\neq 0$$于是任意$A_f$的素理想(其存在性由Zorn引理保证)在$A$中的原像都是一个不含$f$的素理想, 命题得证.   $\square$

Zariski零点定理 对于域$k$, 有限生成$k$-代数$A$, 如果$A$是域, 则$k\subseteq A$是有限域扩张.

证明根据Noether正规化，可以分解为$k\subseteq P\subseteq A$，其中$P$同构于多项式环。注意到因为整性，$A$是域当且仅当$P$是域，从而多项式环$P$必然退化为$k$本身。$\square$

弱零点定理 对于代数闭域$\Bbbk$, $\Bbbk[X_1,\ldots,X_n]$的极大理想都形如$$\left<X_1-x_1,\ldots,X_n-x_n\right>$$其中$x_1,\ldots,x_n\in \Bbbk$.

证明简单的观察知道上述已经构成极大理想。任意取极大理想$\mathfrak{m}$, 考虑$\Bbbk[X_1,\ldots,X_n]/\mathfrak{m}$, 这显然是有限生成$\Bbbk$-代数, 且构成一个域, 根据Zariski零点定理和$\Bbbk$代数闭的假设, $\Bbbk[X_1,\ldots,X_n]/\mathfrak{m}\cong \Bbbk$. 令$x_i$为$X_i$在$\Bbbk$中的像, 那么$\mathfrak{m}\supseteq \left<X_1-x_1,\ldots,X_n-x_n\right>$, 而后者已构成极大理想, 故相等. $\square$

Hilbert零点定理 对于域$k$, 有限生成$k$-代数$A$, 对于$A$的理想$\mathfrak{a}$, 有$$\sqrt{\mathfrak{a}}=\bigcap_{\textrm{极大理想}\mathfrak{m}\supseteq \mathfrak{a}}\mathfrak{m}$$

证明证明方法和schein零点定理如出一辙. 我们要说明最后考虑$A\to A_f$时, 任意$A_f$的极大理想$\mathfrak{m}$的原像$\mathfrak{n}$也是极大理想. 此时可以得到单射$k\to A/\mathfrak{n}\to A/\mathfrak{m}$, 同样, 根据Zariski零点定理, $A/\mathfrak{m}$是$k$的有限扩张, 从而子扩张$A/\mathfrak{n}$自然也是域, 从而$\mathfrak{n}$是极大理想.  $\square$

强零点定理 对于代数闭域$\Bbbk$, 理想$\mathfrak{a}\subseteq \Bbbk[X_1,\ldots,X_n]$. 则$$\mathcal{I}(\mathcal{Z}(\mathfrak{a}))=\sqrt{\mathfrak{a}}$$其中$\mathcal{I}$和$\mathcal{Z}$分别代表子集的理想和理想的零点集。

证明  对于$(x_1,\ldots,x_n)\in \mathbb{A}^n$, $$(x_1,\ldots,x_n)\in \mathcal{Z}(\mathfrak{a})\iff \mathfrak{a}\subseteq \left<X_1-x_1,\ldots,X_n-x_n\right>$$ $$f(x_1,\ldots,x_n)=0\iff f\in \left<X_1-x_1,\ldots,X_n-x_n\right>$$ 故 $$\begin{array}{rll}\mathcal{I}(\mathcal{Z}(\mathfrak{a}))&\displaystyle =\bigcap_{(x_1,\ldots,x_n)\in \mathcal{Z}(\mathfrak{a})}\left<X_1-x_1,\ldots,X_n-x_n\right> & \because \textrm{定义}\\ &\displaystyle = \bigcap_{\left<X_1-x_1,\ldots,X_n-x_n\right>\supseteq \mathfrak{a}}\left<X_1-x_1,\ldots,X_n-x_n\right> & \\ &\displaystyle = \bigcap_{\textrm{极大理想}\mathfrak{m}\supseteq \mathfrak{a}}\mathfrak{m} & \because\textrm{弱零点定理}\\ &\displaystyle = \sqrt{\mathfrak{a}} & \because\textrm{Hilbert零点定理}\end{array}$$ 命题得证. $\square$

通过上行定理，下行定理，以及巧妙运用理想的性质，还可以证明如下推论。

定理令$k$是域, $A$是有限生成$k$-代数整环. 那么$$\dim A=\operatorname{tr.deg}_k \operatorname{Frac} A$$且任意$A$的素理想$\mathfrak{p}$都有$$\dim A=\dim A_{\mathfrak{p}}+\dim A/\mathfrak{p}$$换言之, 一条素理想升链$$\mathfrak{p}_0\subsetneqq \ldots \subsetneqq\mathfrak{p}_r$$使得$r=\dim A$当且仅当这条链是极长的. 这种性质被称为是链式(catenary)的。