本文主要是介绍第十章《搞懂算法:支持向量机是怎么回事》笔记，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
支持向量机(Support Vector Machine，SVM )主要用于分类问题的处理。
10.1 SVM有什么用
SVM 的分类效果很 好，适用范围也较广，但模型的可解释性较为一般。
SVM 根据线性可分的程度不同，可以分为 3 类:线性可分 SVM、线性 SVM 和非线性 SVM。
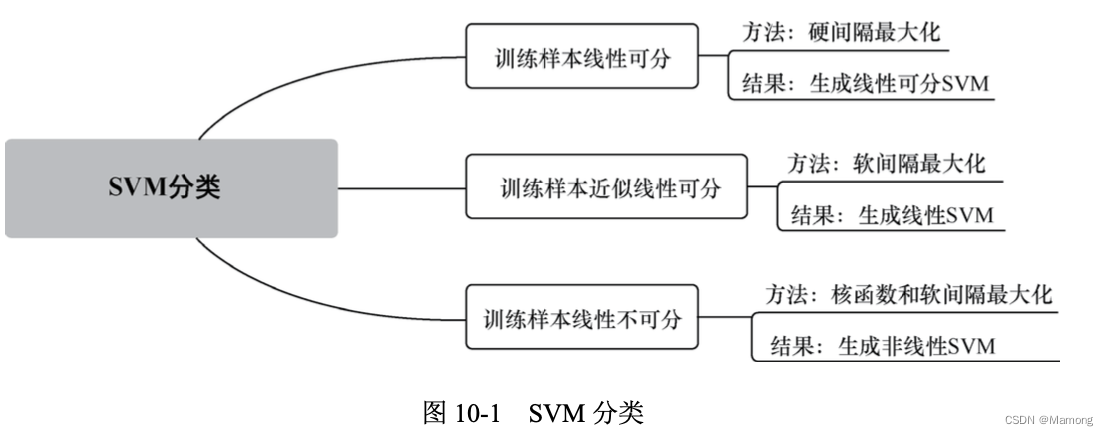
10.2 SVM算法原理和过程是什么
样本数据的特征向量构成了一 个空间，每个样本点都占据空间中的一个位置。如果有一条线、一个面或者一个特殊形状将样本数据分割成两部分，其中一部分为正样本，另一部分为负样本，这样就太美好了。因为我们把新数据的特征向量跟这个分割线(面)进行比较，就可以判断新数据是正样本还是负样本了，也就实现了对新数据的分类。这样的一个分割线(面)就叫作超平面。所以采用 SVM 的目的就 是找到这样一个超平面。
但大多数时候，满足这样条件的超平面(分割线)不是唯一的，而是有多个。分割线更加远离正、负样本数据点，具有更好和更稳定的分类效果，这就是我们想寻找的分离超平面。
10.2.1 分离超平面是什么
一般来说，SVM 中把这种对正、负样本进行分割的操作叫作“分离超平面”。分离超平面在不同维度上表现的形态 不同。
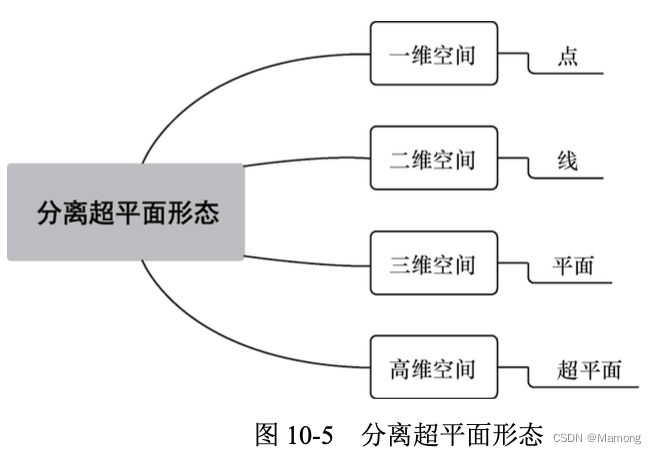
最佳分离超平面的判断标准，是间隔与支持向量。
10.2.2 间隔与支持向量是什么
理想的分离超平面应该具有这样的特点:能够分割正、负样本，但同时尽可能远离所有样本数据点。
三维空间中，任何一个平面都可以用 Ax+By+Cz+D=0 来表示，于是点 (x0 , y0 , z0) 到该平面
的距离为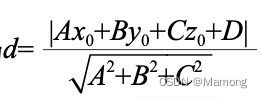
，一维空间和二维空间也类似。
。分别是一维空间、二维空间、三维空间中的范数，被记 作 ‖w‖。
假设超平面能够将样本正确分类，那么距离超平面最近的几个训练样本数据点被称为“支持向量”。
两个不同类支持向量到分离超平面的距离之和为
，这个距离被称为“间隔”。
最佳分离超平面就是“间隔”最大的分离超平面，而要想找到“最大间隔”的分离超平面，就要找到满足约束条件(将样本分为两类)的参数 w 和 b，使得 γ 取到最大值。
解决线性不可分的方法就是使用核函数。核函数解决线性不可分的本质思想就 是把原始样本通过核函数映射到高维空间中，从而让样本在高维空间中成为线性可分的，然后 再使用常见的线性分类器进行分类。
n 维空间上线性不可分的问题可以通过升维到 n+1 维空间中构造新的分类函数并使其在 n 维空间上的投影对样本数据点进行分类来解决。SVM 中 这种通用的升维方法就是核函数，常见的核函数有线性核函数、多项式核函数、径向基核函数(RBF 核函数)、高斯核函数等。
10.3 编程实践:手把手教你写代码
这篇关于第十章《搞懂算法:支持向量机是怎么回事》笔记的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
