本文主要是介绍CF 659 A方向 B排序 C暴力 D方向 E并查集/无向环的dfs/无向环的染色bfs F并查集+dfs/bfs G:递推,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
http://codeforces.com/contest/659
自己写了以后然后看了一下大牛们的代码,发现还有好多步骤可以简化,自己写的过于冗长了。。。慢慢来吧。。。
Vasya lives in a round building, whose entrances are numbered sequentially by integers from 1 to n. Entrance n and entrance 1 are adjacent.
Today Vasya got bored and decided to take a walk in the yard. Vasya lives in entrance a and he decided that during his walk he will move around the house b entrances in the direction of increasing numbers (in this order entrance n should be followed by entrance 1). The negative value of b corresponds to moving |b| entrances in the order of decreasing numbers (in this order entrance 1 is followed by entrance n). If b = 0, then Vasya prefers to walk beside his entrance.
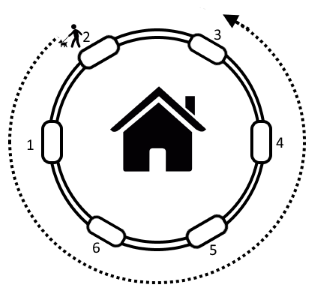 Illustration for n = 6, a = 2, b = - 5.
Illustration for n = 6, a = 2, b = - 5. Help Vasya to determine the number of the entrance, near which he will be at the end of his walk.
The single line of the input contains three space-separated integers n, a and b (1 ≤ n ≤ 100, 1 ≤ a ≤ n, - 100 ≤ b ≤ 100) — the number of entrances at Vasya's place, the number of his entrance and the length of his walk, respectively.
Print a single integer k (1 ≤ k ≤ n) — the number of the entrance where Vasya will be at the end of his walk.
6 2 -5
3
5 1 3
4
3 2 7
3
The first example is illustrated by the picture in the statement
#includeusing namespace std;
const int inf = 0x3f3f3f3f;
typedef long long ll;
int main(){
int n, a, b;
scanf("%d%d%d", &n, &a, &b);
while (abs(b) > n){
if (b > 0) b -= n;
else b += n;
}
int tmp = a + b;
while (abs(tmp) > n){
if (tmp > 0) tmp -= n;
else tmp += n;
}
if (tmp <= 0) printf("%d\n", n+tmp);
else printf("%d\n", tmp);
return 0;
}Very soon Berland will hold a School Team Programming Olympiad. From each of the m Berland regions a team of two people is invited to participate in the olympiad. The qualifying contest to form teams was held and it was attended by n Berland students. There were at least two schoolboys participating from each of the m regions of Berland. The result of each of the participants of the qualifying competition is an integer score from 0 to 800 inclusive.
The team of each region is formed from two such members of the qualifying competition of the region, that none of them can be replaced by a schoolboy of the same region, not included in the team and who received a greater number of points. There may be a situation where a team of some region can not be formed uniquely, that is, there is more than one school team that meets the properties described above. In this case, the region needs to undertake an additional contest. The two teams in the region are considered to be different if there is at least one schoolboy who is included in one team and is not included in the other team. It is guaranteed that for each region at least two its representatives participated in the qualifying contest.
Your task is, given the results of the qualifying competition, to identify the team from each region, or to announce that in this region its formation requires additional contests.
The first line of the input contains two integers n and m (2 ≤ n ≤ 100 000, 1 ≤ m ≤ 10 000, n ≥ 2m) — the number of participants of the qualifying contest and the number of regions in Berland.
Next n lines contain the description of the participants of the qualifying contest in the following format: Surname (a string of length from 1to 10 characters and consisting of large and small English letters), region number (integer from 1 to m) and the number of points scored by the participant (integer from 0 to 800, inclusive).
It is guaranteed that all surnames of all the participants are distinct and at least two people participated from each of the m regions. The surnames that only differ in letter cases, should be considered distinct.
Print m lines. On the i-th line print the team of the i-th region — the surnames of the two team members in an arbitrary order, or a single character "?" (without the quotes) if you need to spend further qualifying contests in the region.
5 2 Ivanov 1 763 Andreev 2 800 Petrov 1 595 Sidorov 1 790 Semenov 2 503
Sidorov Ivanov Andreev Semenov
5 2 Ivanov 1 800 Andreev 2 763 Petrov 1 800 Sidorov 1 800 Semenov 2 503
? Andreev Semenov
In the first sample region teams are uniquely determined.
In the second sample the team from region 2 is uniquely determined and the team from region 1 can have three teams: "Petrov"-"Sidorov", "Ivanov"-"Sidorov", "Ivanov" -"Petrov", so it is impossible to determine a team uniquely.
来自同一个城市的人,只能出最高的两个,如果一个城市<=1或者是这个城市最高的几个人分数相等,那么就输出?,否则就输出名字
思路:
用vector储存,然后排序一下就好了
#includeusing namespace std;
const int inf = 0x3f3f3f3f;
typedef long long ll;
struct body{
string name;
int num;
};
int n, m;
vector a[10000 + 5];
bool cmp(const body x, const body y){
return x.num > y.num;
}
int main(){
while (scanf("%d%d", &n, &m) == 2){
for (int i = 0; i < n; i++){
body tmp;
int p;
cin >> tmp.name >> p >> tmp.num;
a[p].push_back(tmp);
}
for (int i = 1; i <= m; i++){
sort(a[i].begin(), a[i].end(), cmp);
int tmp = a[i].size();
if (tmp >= 3){
if (a[i][1].num == a[i][2].num ){
printf("?\n");
continue;
}
else {
cout << a[i][0].name << " " << a[i][1].name << endl;
}
}
else if (tmp == 2){
cout << a[i][0].name << " " <<< endl;
}
else printf("?\n");
a[i].erase(a[i].begin(), a[i].end());
}
}
return 0;
}In Berland recently a new collection of toys went on sale. This collection consists of 109 types of toys, numbered with integers from 1 to109. A toy from the new collection of the i-th type costs i bourles.
Tania has managed to collect n different types of toys a1, a2, ..., an from the new collection. Today is Tanya's birthday, and her mother decided to spend no more than m bourles on the gift to the daughter. Tanya will choose several different types of toys from the new collection as a gift. Of course, she does not want to get a type of toy which she already has.
Tanya wants to have as many distinct types of toys in her collection as possible as the result. The new collection is too diverse, and Tanya is too little, so she asks you to help her in this.
The first line contains two integers n (1 ≤ n ≤ 100 000) and m (1 ≤ m ≤ 109) — the number of types of toys that Tanya already has and the number of bourles that her mom is willing to spend on buying new toys.
The next line contains n distinct integers a1, a2, ..., an (1 ≤ ai ≤ 109) — the types of toys that Tanya already has.
In the first line print a single integer k — the number of different types of toys that Tanya should choose so that the number of different types of toys in her collection is maximum possible. Of course, the total cost of the selected toys should not exceed m.
In the second line print k distinct space-separated integers t1, t2, ..., tk (1 ≤ ti ≤ 109) — the types of toys that Tanya should choose.
If there are multiple answers, you may print any of them. Values of ti can be printed in any order.
3 7 1 3 4
2 2 5
4 14 4 6 12 8
4 7 2 3 1
In the first sample mom should buy two toys: one toy of the 2-nd type and one toy of the 5-th type. At any other purchase for 7 bourles (assuming that the toys of types 1, 3 and 4 have already been bought), it is impossible to buy two and more toys.
题目大意:
有无穷个玩具,第i个玩具要i元,妈妈一共有m元,且女儿刚开始就有了n个玩具,并且妈妈购买的时候不能再购买这ni个玩具。
思路:
由于最大是10^9,不过10W*5W的值就超过10E很多了,所以枚举的最大就是约等于10W左右,然后跳过有了的这n个玩具就可以了
#includeusing namespace std;
const int inf = 0x3f3f3f3f;
typedef long long ll;
vector a;
int n, m;
/*
int cal(int m){
double t = sqrt(8 * m + 1);
return (t - 1) / 2;
}
*/
int main(){
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++){
int x;
scanf("%d", &x);
a.push_back(x);
}
sort(a.begin(), a.end());
int cnt = 0, sum = 0;
int d = 0;
vector ind;
for (int i = 1; sum + i <= m; i++){
if (i == a[d]){
d++;
continue;
}
cnt++;
sum += i;
ind.push_back(i);
}
printf("%d\n", cnt);
for (int i = ind.size() - 1; i >= 0; i--){
printf("%d%c", ind[i], i == 0 ? '\n' : ' ');
}
return 0;
}Maria participates in a bicycle race.
The speedway takes place on the shores of Lake Lucerne, just repeating its contour. As you know, the lake shore consists only of straight sections, directed to the north, south, east or west.
Let's introduce a system of coordinates, directing the Ox axis from west to east, and the Oy axis from south to north. As a starting position of the race the southernmost point of the track is selected (and if there are several such points, the most western among them). The participants start the race, moving to the north. At all straight sections of the track, the participants travel in one of the four directions (north, south, east or west) and change the direction of movement only in bends between the straight sections. The participants, of course, never turn back, that is, they do not change the direction of movement from north to south or from east to west (or vice versa).
Maria is still young, so she does not feel confident at some turns. Namely, Maria feels insecure if at a failed or untimely turn, she gets into the water. In other words, Maria considers the turn dangerous if she immediately gets into the water if it is ignored.
Help Maria get ready for the competition — determine the number of dangerous turns on the track.
The first line of the input contains an integer n (4 ≤ n ≤ 1000) — the number of straight sections of the track.
The following (n + 1)-th line contains pairs of integers (xi, yi) ( - 10 000 ≤ xi, yi ≤ 10 000). The first of these points is the starting position. The i-th straight section of the track begins at the point (xi, yi) and ends at the point (xi + 1, yi + 1).
It is guaranteed that:
- the first straight section is directed to the north;
- the southernmost (and if there are several, then the most western of among them) point of the track is the first point;
- the last point coincides with the first one (i.e., the start position);
- any pair of straight sections of the track has no shared points (except for the neighboring ones, they share exactly one point);
- no pair of points (except for the first and last one) is the same;
- no two adjacent straight sections are directed in the same direction or in opposite directions.
Print a single integer — the number of dangerous turns on the track.
6 0 0 0 1 1 1 1 2 2 2 2 0 0 0
1
16 1 1 1 5 3 5 3 7 2 7 2 9 6 9 6 7 5 7 5 3 4 3 4 4 3 4 3 2 5 2 5 1 1 1
6
The first sample corresponds to the picture:
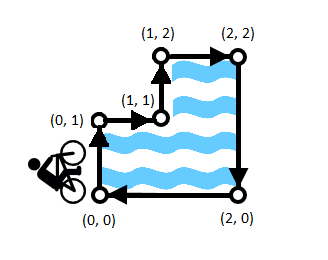
The picture shows that you can get in the water under unfortunate circumstances only at turn at the point (1, 1). Thus, the answer is 1.
题目大意:
有n个点,每次都是只能往东南西北走,并且刚开始的方向一定是往北面走。按照这些点走,有些点,如果不转弯的话就会调入水中。问,这样的点有几个
思路:
因为每次会落入水中的话,都是一定是往左边拐弯,所以只要统计出有几个点是往左边走的就可以了
#includeusing namespace std;
vector d;
vector > vec;
int main(){
int n;
scanf("%d", &n);
while (n--){
int a, b;
scanf("%d%d", &a, &b);
vec.push_back(make_pair(a, b));
}
int l = vec.size();
for (int i = 0; i < l-1; i++){
int cnt = 0;
int x = vec[i+1].first;
int y = vec[i+1].second;
if (vec[i].first == x && vec[i].second < y) cnt = 0;
else if (vec[i].first == x && vec[i].second > y) cnt = 2;
else if (vec[i].second == y && vec[i].first < x) cnt = 1;
else cnt = 3;
d.push_back(cnt);
}
l = d.size();
int cnt = 0;
for (int i = 0; i < l-1; i++){
int now = d[i];
int next = d[i+1];
int tmp = (now + 3) % 4;
if (next == tmp) cnt++;
}
printf("%d\n", cnt);
return 0;
}有m条无向边和n个顶点。问,如果把这些无向边换成有向边,那么,入度<1的顶点有几个
思路:
如果能够形成环,那么入度<1的不存在,即0.
如果不能形成环,则顶点数=边数-1,入度小于1的最小的数目是1.
另外还要特别的判断一下,可能存在多棵树。
起初我是打算用dfs的,但是看了一下大牛的代码,发现只要利用关系就可以了,不一定需要dfs,不过如果要使用dfs的话,为了不让一条边走来回,就要用dfs(int i, int pos),判断会不会形成环,或者是用bfs的环形染色法判断
#includeusing namespace std;
const int maxn = 100000 + 5;
int n, m;
bool used[maxn];
int par[maxn];
int edge, cnt;
int x[maxn];
int a[maxn], b[maxn];
int sear(int x){
if (par[x] == x) return x;
return par[x] = sear(par[x]);
}
void unite(int x, int y){
x = sear(x);
y = sear(y);
if (x == y) return ;
if (x < y){
par[y] = x;
}
else par[x] = y;
}
int main(){
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++){
par[i] = i;
}
bool flag = 0;
edge = cnt = 0;
for (int i = 1; i <= m; i++){
int v;
scanf("%d%d", x + i, &v);
unite(x[i], v);
}
for (int i = 1; i <= n; i++){
a[sear(i)]++;
}
for (int i = 1; i <= m; i++){
b[sear(x[i])]++;
}
int ans = 0;
for (int i = 1; i <= n; i++){
if (b[i] == a[i]-1) ans++;
}
printf("%d\n", ans);
return 0;
}#includeusing namespace std;
typedef long long ll;
typedef pairP;
const int maxn = 100000 + 5;
int par[maxn];
int d[maxn];
bool vis[maxn];
int n, m;
struct Edge{
int from, to;
Edge (int from, int to): from(from), to(to){}
};
vector edges;
vector G[maxn];
void init(){
scanf("%d%d", &n, &m);
for (int i = 0; i <= n; i++){
G[i].erase(G[i].begin(), G[i].end());
vis[i] = false;
d[i] = 0;
}
edges.erase(edges.begin(), edges.end());
for (int i = 0; i < m; i++){
int u, v;
scanf("%d%d", &u, &v);
edges.push_back(Edge(u, v));
edges.push_back(Edge(v, u));
int l = edges.size();
G[u].push_back(l - 2);
G[v].push_back(l - 1);
}
}
void solve(){
int res = 0;
for (int i = 1; i <= n; i++){
if (vis[i] == true) continue;
bool flag = true;
queue que; que.push(i); vis[i] = true; d[i] = 1; while (!que.empty()){ int s = que.front(); que.pop(); d[s] = 2; int cnt = 0; for (int j = 0; j < G[s].size(); j++){ Edge x = edges[G[s][j]]; if (d[x.to] >= 1) { cnt++; continue; } vis[x.to] = true; que.push(x.to); d[x.to] = 2; } if (cnt >= 2) flag = false; } //printf("flag = %d\n", flag); res += flag; } printf("%d\n", res); } int main(){ init(); solve(); return 0; } The farmer Polycarp has a warehouse with hay, which can be represented as an n × m rectangular table, where n is the number of rows, and m is the number of columns in the table. Each cell of the table contains a haystack. The height in meters of the hay located in the i-th row and the j-th column is equal to an integer ai, j and coincides with the number of cubic meters of hay in the haystack, because all cells have the size of the base 1 × 1. Polycarp has decided to tidy up in the warehouse by removing an arbitrary integer amount of cubic meters of hay from the top of each stack. You can take different amounts of hay from different haystacks. Besides, it is allowed not to touch a stack at all, or, on the contrary, to remove it completely. If a stack is completely removed, the corresponding cell becomes empty and no longer contains the stack.
Polycarp wants the following requirements to hold after the reorganization:
- the total amount of hay remaining in the warehouse must be equal to k,
- the heights of all stacks (i.e., cells containing a non-zero amount of hay) should be the same,
- the height of at least one stack must remain the same as it was,
- for the stability of the remaining structure all the stacks should form one connected region.
The two stacks are considered adjacent if they share a side in the table. The area is called connected if from any of the stack in the area you can get to any other stack in this area, moving only to adjacent stacks. In this case two adjacent stacks necessarily belong to the same area.
Help Polycarp complete this challenging task or inform that it is impossible.
The first line of the input contains three integers n, m (1 ≤ n, m ≤ 1000) and k (1 ≤ k ≤ 1018) — the number of rows and columns of the rectangular table where heaps of hay are lain and the required total number cubic meters of hay after the reorganization.
Then n lines follow, each containing m positive integers ai, j (1 ≤ ai, j ≤ 109), where ai, j is equal to the number of cubic meters of hay making the hay stack on the i-th row and j-th column of the table.
In the first line print "YES" (without quotes), if Polycarpus can perform the reorganisation and "NO" (without quotes) otherwise. If the answer is "YES" (without quotes), then in next n lines print m numbers — the heights of the remaining hay stacks. All the remaining non-zero values should be equal, represent a connected area and at least one of these values shouldn't be altered.
If there are multiple answers, print any of them.
2 3 35 10 4 9 9 9 7
YES 7 0 7 7 7 7
4 4 50 5 9 1 1 5 1 1 5 5 1 5 5 5 5 7 1
YES 5 5 0 0 5 0 0 5 5 0 5 5 5 5 5 0
2 4 12 1 1 3 1 1 6 2 4
NO
In the first sample non-zero values make up a connected area, their values do not exceed the initial heights of hay stacks. All the non-zero values equal 7, and their number is 5, so the total volume of the remaining hay equals the required value k = 7·5 = 35. At that the stack that is on the second line and third row remained unaltered.
#includeusing namespace std;
const int maxn = 1000 + 5;
typedef long long ll;
int n, m, cnt;
ll lim;
int l[maxn * maxn];
int par[maxn * maxn], vis[maxn][maxn];
vector > vec;
int dx[] = {1, -1, 0, 0};
int dy[] = {0, 0, -1 ,1};
struct point{
int x, y;
int val;
bool operator < (const point &p) const{
return val > p.val;
}
}atlas[maxn * maxn];
int findp(int x){
if (par[x] == x) return x;
return par[x] = findp(par[x]);
}
void dfs(int x, int y){
if (vis[x][y] == 0) return ;
vis[x][y] = 0;
vec.push_back(make_pair(x, y));
for (int i = 0; i < 4; i++){
int nx = x + dx[i];
int ny = y + dy[i];
if (nx < 0 || nx >= n || ny < 0 || ny >= m) continue;
if (vis[nx][ny])
dfs(nx, ny);
}
}
void solve(){
ll res = -1;
int lo = 0;
int a, b;
for (int i = 0; i < n * m; i++){
int x = atlas[i].x;
int y = atlas[i].y;
vis[x][y] = 1;
for (int j = 0; j < 4; j++){
//printf("haha\n");
int nx = x + dx[j];
int ny = y + dy[j];
if (nx < 0 || nx >= n || ny < 0 || ny >= m) continue;
if (vis[nx][ny] == 0) continue;
a = findp(x * m + y);
b = findp(nx * m + ny);
if (b != a){
par[b] = a;
l[a] += l[b];
}
}
if (lim % atlas[i].val == 0 && l[x * m + y] >= lim / atlas[i].val){
dfs(x, y);
res = atlas[i].val;
lo = lim / atlas[i].val;
break;
}
}
if (res == -1){
printf("NO\n");
return ;
}
else printf("YES\n");
memset(vis, 0, sizeof(vis));
for (int i = 0; i < lo; i++){
int x = vec[i].first, y = vec[i].second;
vis[x][y] = 1;
}
for (int i = 0; i < n; i++){
for (int j = 0; j < m; j++){
if (vis[i][j]) printf("%d", res);
else printf("%d", 0);
printf("%c", j == m-1 ? '\n' : ' ');
}
}
}
void init(){
scanf("%d%d%I64d", &n, &m, &lim);
for (int i = 0; i < n; i++){
for (int j = 0; j < m; j++){
int tmp;
scanf("%d", &tmp);
atlas[i*m + j].x = i;
atlas[i*m + j].y = j;
atlas[i*m + j].val = tmp;
}
}
sort(atlas, atlas + n * m);
for (int i = 0; i < n * m; i++){
par[i] = i;
l[i] = 1;
}
}
int main(){
init();
solve();
return 0;
}
Long ago, Vasily built a good fence at his country house. Vasily calls a fence good, if it is a series of n consecutively fastened vertical boards of centimeter width, the height of each in centimeters is a positive integer. The house owner remembers that the height of thei-th board to the left is hi.
Today Vasily decided to change the design of the fence he had built, by cutting his top connected part so that the fence remained good. The cut part should consist of only the upper parts of the boards, while the adjacent parts must be interconnected (share a non-zero length before cutting out of the fence).
You, as Vasily's curious neighbor, will count the number of possible ways to cut exactly one part as is described above. Two ways to cut a part are called distinct, if for the remaining fences there is such i, that the height of the i-th boards vary.
As Vasily's fence can be very high and long, get the remainder after dividing the required number of ways by 1 000 000 007 (109 + 7).
The first line contains integer n (1 ≤ n ≤ 1 000 000) — the number of boards in Vasily's fence.
The second line contains n space-separated numbers h1, h2, ..., hn (1 ≤ hi ≤ 109), where hi equals the height of the i-th board to the left.
Print the remainder after dividing r by 1 000 000 007, where r is the number of ways to cut exactly one connected part so that the part consisted of the upper parts of the boards and the remaining fence was good.
2 1 1
0
3 3 4 2
13
From the fence from the first example it is impossible to cut exactly one piece so as the remaining fence was good.
All the possible variants of the resulting fence from the second sample look as follows (the grey shows the cut out part):

题目大意:
给n个高度为h的紧挨着的木条,现在,我们要将木条分别砍断
①砍断的每块木条之间必须是连通的
②每块木条的长度在砍断前后都不能为0
思路:
我们定义一个cal(l,r),然后l代表的是left,r是right。cal所计算的就是在l和r之间一共可以有几组这样的连通块。
当l==r的时候,连通块的个数就等于h[l]-1
当l!=r的时候我们我们可以得到
cal(l,r) = min(h[l], h[l + 1]) * min(h[r], h[r - 1]) * π min(h[i], h[i + 1], h[i - 1])(l+1 <= i <= r -1);
然后我们可以得出

最后,我们定义成

然后通过递推公式S(r + 1) = S(r) × min(hr - 1 - 1, hr - 1, hr + 1 - 1) + min(hr - 1, hr + 1 - 1).得出值就可以了
#includeusing namespace std;
typedef long long ll;
const int maxn = 1000000 + 5;
const ll inf = 0x3f3f3f3f;
const ll mod = 1000000007;
ll n;
ll h[maxn];
ll s[maxn];
int main(){
while (scanf("%I64d", &n) == 1){
memset(h, 0, sizeof(h));
for (int i = 1; i <= n; i++){
scanf("%I64d", h + i);
h[i]--;
}
ll res = 0;
memset(s, 0, sizeof(s));
for (int i = 1; i <= n; i++){
s[i + 1] = (s[i] * min(h[i - 1], min(h[i], h[i + 1])) + min(h[i], h[i + 1])) % mod;
res = (res + s[i + 1] * min(h[i], h[i + 1])) % mod;
}
for (int i = 1; i <= n; i++){
res += h[i];
res %= mod;
}
printf("%I64d\n", res);
}
return 0;
}
这篇关于CF 659 A方向 B排序 C暴力 D方向 E并查集/无向环的dfs/无向环的染色bfs F并查集+dfs/bfs G:递推的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!
 ,
,  ,
,  .
. ,
,  ,
,  ,
,  ,
,  ,
,  .
.




