最少砝码/砝码天平类规律

题解：

其实这道题考的就是规律，只要找到规律这道题就是相当于加减乘除的难度级别了。但题目给出的样例混淆了人们的思维方式。

1个砝码只能称1这个重量，所以此时能称重的最大重量为1；

两个砝码时有以下情况：

1，2：1 = 1，2 = 2，3 = 1+2最大能称重到3；

1，3：1 = 1，2 = 3-1，3 = 3，4 = 1+3最大能称重的重量到4；

1，4：1 = 1，2无解，所以从4往后都都无法计算出2的重量。

所以两个砝码时，即（1，3）能称重的最大重量为4。

然后一次往后递推，可以得出三个砝码时（1，3，9）能称重的最大重量为13。

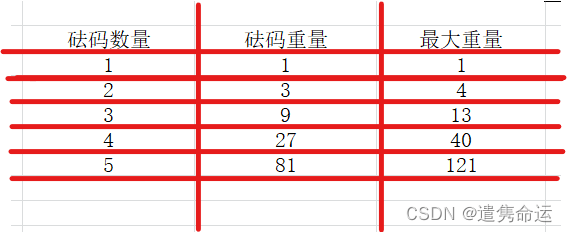
所以如下图，容易得出新增砝码的重量等于上一个砝码重量的三倍，最大重量就等于增加最后的砝码之前最大重量加上新增的砝码重量。

砝码数量：count每次递增一

砝码重量：weight *= 3 ，即上一个砝码的三倍重量即为新增砝码的重量

最大重量：total += weight，即增加砝码之前的最大重量加上新增砝码的重量

## 解题思路请填写解题思路```
import os
import sys# 请在此输入您的代码
n=int(input())
count=1
weight=1
maxNum=1
while maxNum<n:count+=1weight*=3maxNum+=weight 
print(count)
```