求极限Lim x-＞0 (x-sinx)*e-²x / (1-x)⅓

本文主要是介绍求极限Lim x-＞0 (x-sinx)*e-²x / (1-x)⅓，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

题目如下：

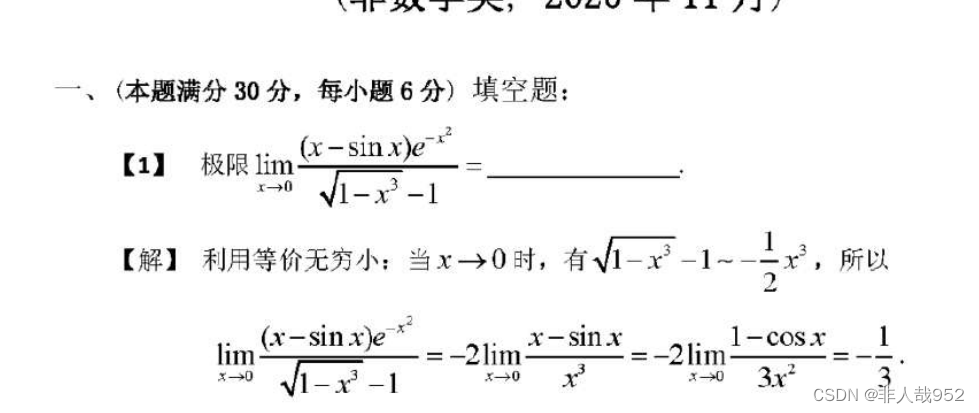
解题思路:

这题运用了无穷小替换、洛必达法则、求导法则

具体解题思路如下:

1、首先带入x趋近于0，可以得到（0*1）/0，所以可以把e的-x的平方沈略掉

然后根据无穷小替换，利用t趋近于0时，(1+t)的n分之一次方 趋近于t/n

此题中替换 (1+(-x的3次方))的二分之一次方，变成-x的平方/2

3、然后洛必达法则，“0/0型” 分子分母同事求导，极限值不变

这篇关于求极限Lim x-＞0 (x-sinx)*e-²x / (1-x)⅓的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---