BSG白山极客挑战赛D 解题报告

这题关键当然就在那个非常神的性质。

其实，对于一棵树来说，我们在上面随便找一个点（可以是边上的点任意一点），也就是可以选无穷多个点，那么距离这个点最远的点一定是一条直径的一端。且任意一条直径都存在一个端点是距离这个点最远的点。
我们考虑距离任意一点x最远的点y，假设有一条直径是(a,b)。（下面我们用(a,b)来表示两点之间的路径，用|(a,b)|来表示这条路径的长度）。
那么我们分两种情况考虑。
如果$(a,b)\cap (x,y)=\varnothing$，如图。因为y距离x最远，所以$|(d,y)|\ge |(d,a)|,|(d,y)|\ge |(d,b)|$；因为(a,b)是直径，所以$|(b,c)|\ge|(c,y)|,|(a,c)|\ge|(c,y)|$，所以$|(d,y)|\ge|(b,d)|>|(b,c)|\ge|(c,y)|>|(d,y)|$，产生了矛盾，所以这种情况其实是不存在的。
如果$(a,b)\cap (x,y)\not=\varnothing$，如图。因为y距离x最远，所以$|(d,y)|\ge|(d,b)|$，因为(a,b)是直径，所以$|(d,y)|\le |(d,b)|$，所以$|(d,y)|=|(d,b)|$。即(a,y)也是一条直径。

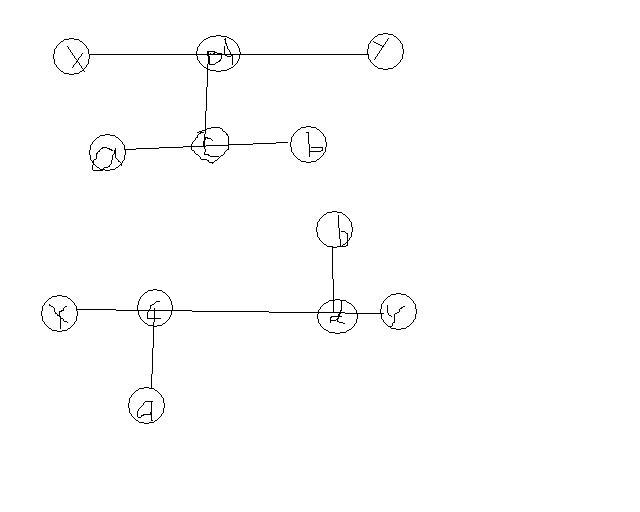
根据这个性质就有一个经典的找直径的算法，就是随便找一个点找离它最远的点，那么它必然是一条直径的一端，而离它最远的点就是直径的另一端了，所以只需要两边dfs/bfs即可。

那么这一题需要说明的是对于两个点集S、T，任选$x\in S,y\in T$，则距离最远的(x,y)中存在$y\in \{ a,b \}$((a,b)是T的一条直径)，那么对称的x也一样。
其实在S中任选一个点x出发，设其在T中距离最远的点为y，(x,y)上最靠近x的存在于T中两点路径上的点为z。那么y显然必须是离z最远的点，而根据上面的分析，一条直径必然有一个端点是离z最远的点。

那么这个问题就变成了求出一段区间的直径，题解说是可以用线段树$O(\log n)$预处理，$O(1)$查询，我表示完全没看懂。。
我的做法是先用st表预处理出lca，因为合并两个区间的时候显然需要O(1)查询两点距离什么的。然后再用st表预处理出长为$2^i$的区间的直径。时间复杂度$O(6n\log n)-O(6m)$。

代码：

#include<cstdio>
#include<iostream>
using namespace std;
#include<algorithm>
void in(int &x){char c=getchar();while(c<'0'||c>'9')c=getchar();for(x=0;c>='0'&&c<='9';c=getchar())x=x*10+(c^'0');
}
const int N=1e5+5;
int next[N<<1],succ[N<<1],w[N<<1],ptr[N],etot=1;
void addedge(int from,int to,int wt){next[etot]=ptr[from],ptr[from]=etot,succ[etot]=to,w[etot++]=wt;
}const int Log=18;
int fa[N],depth[N];
int d[N<<1],dfn[N];
int Min(const int &a,const int &b){return depth[a]<depth[b]?a:b;
}
int dtot=1;
int dis[N];
int stack[N],cur[N];
void dfs(){stack[0]=1;depth[1]=1;for(int top=1,node;top--;){node=stack[top];//printf("-----%d----\n",node);if(cur[node]!=ptr[node]){d[dtot]=node;dfn[node]=dtot++;}if(cur[node]){++top;if(succ[cur[node]]!=fa[node]){depth[succ[cur[node]]]=depth[node]+1;dis[succ[cur[node]]]=dis[node]+w[cur[node]];fa[succ[cur[node]]]=node;stack[top++]=succ[cur[node]];}cur[node]=next[cur[node]];}}
}
int lca[Log][N<<1];
int lg[N<<1];
int querydis(int a,int b){if(dfn[a]>dfn[b])swap(a,b);int tmplg=lg[dfn[b]-dfn[a]+1],x=Min(lca[tmplg][dfn[a]],lca[tmplg][dfn[b]-(1<<tmplg)+1]);//printf("Min%d:(%d,%d)\n",tmplg,dfn[a],dfn[b]-(1<<tmplg)+1);//printf("dis(%d,%d),%d=%d\n",a,b,x,dis[a]+dis[b]-(dis[x]<<1));return dis[a]+dis[b]-(dis[x]<<1);
}
struct AS{int a[2];
}st[Log][N];
AS merge(const AS & u,const AS &v){int maxdis=querydis(u.a[0],u.a[1]),tmp;AS ans=u;if((tmp=querydis(v.a[0],v.a[1]))>maxdis){maxdis=tmp;ans=v;//printf("Get:%d\n",maxdis);}for(int i=2;i--;)for(int j=2;j--;)if((tmp=querydis(u.a[i],v.a[j]))>maxdis){maxdis=tmp;ans=(AS){u.a[i],v.a[j]};}//printf("merge((%d,%d),(%d,%d))=(%d,%d)\n",u.a[0],u.a[1],v.a[0],v.a[1],ans.a[0],ans.a[1]);return ans;
}
AS query(int l,int r){int tmplg=lg[r-l+1];//printf("[%d,%d]\n",l,r);//printf("merge(%d,(%d,%d))\n",tmplg,l,r-(1<<tmplg)+1);//printf("%d %d\n",st[tmplg][l].a[0],st[tmplg][l].a[1]);return merge(st[tmplg][l],st[tmplg][r-(1<<tmplg)+1]);
}
int main(){freopen("51noded.in","r",stdin);//freopen("51noded.out","w",stdout);int n;in(n);int x,y,z;for(int i=n;--i;){in(x),in(y),in(z);addedge(x,y,z),addedge(y,x,z);}dtot=1;for(int i=n;i;--i)cur[i]=ptr[i];dfs();//cout<<dfn[65536]<<endl;//cout<<d[68211]<<endl;/*puts("----dfn----");for(int i=1;i<dtot;++i)printf("%d ",d[i]);puts("");*///cout<<d[68211]<<endl;for(int i=dtot;--i;)lca[0][i]=d[i];for(int i=1,j=0;i<dtot;++i){lg[i]=j;if(i==1<<j+1)++j;}//cout<<lca[0][68211]<<endl;for(int j=1;j<Log;++j)for(int i=dtot-(1<<j);i>0;--i)lca[j][i]=Min(lca[j-1][i],lca[j-1][i+(1<<j-1)]);/*for(int j=0;j<Log;++j)for(int i=dtot-(1<<j);i>0;--i)printf("lca(%d,%d)=%d\n",j,i,lca[j][i]);*/for(int i=1;i<=n;++i)st[0][i]=(AS){i,i};for(int j=1;j<Log;++j)for(int i=n-(1<<j)+1;i>0;--i)st[j][i]=merge(st[j-1][i],st[j-1][i+(1<<j-1)]);//printf("%d %d\n",st[15][1].a[0],st[15][1].a[1]);//printf("%d %d\n",st[0][65895].a[0],st[0][65895].a[1]);//printf("%d %d\n",st[0][65896].a[0],st[0][65896].a[1]);//cout<<Min(lca[0][68211],lca[0][68211])<<endl;//testquery(65895,65895);int m;in(m);int a,b,c,d;AS s,t;while(m--){in(a),in(b),in(c),in(d);s=query(a,b),t=query(c,d);//printf("s=%d,%d\n",s.a[0],s.a[1]);//printf("t=%d,%d\n",t.a[0],t.a[1]);int maxdis=0;for(int i=2;i--;)for(int j=2;j--;)maxdis=max(maxdis,querydis(s.a[i],t.a[j]));printf("%d\n",maxdis);}
}

总结：
①一定要记得检查数组大小！
②对于树T的任意一条直径(a,b)，$\forall x\in T$，必然有$max(|(a,x)|,|(b,x)|)\ge max\{|(x,y)\}(\forall y \in T)$.