本文主要是介绍2023年辽宁省数学建模竞赛B题思路详细分析,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
摘要略,2023年辽宁省数学建模竞赛B题代码和论文已经完成,代码为全部3问代码,论文包括摘要、问题重述、问题分享、模型假设、符号说明、模型的建立和求解(问题1无监督聚类模型的建立和求解,问题二有监督分类预测模型的建立和求解、问题三迁移预测模型的建立与适用性评估)、模型的评价、参考文献、附录,详情参考见文末
二、 问题重述
2023辽宁省数学建模竞赛B题:“海洋强国”战略部署已成为推动中国现代化建设的重要组成部分,国家对此提出“发展海洋经济,保护海洋生态环境,加快建设海洋强国”的明确要求。 《辽宁省“十四五”海洋经济发展规划》明确未来全省海洋经济的发展战略、发展目标、重大任务、空间部署和保障措施。规划范围包括辽宁省全部海域和大连、丹东、锦州、营口、盘锦和葫芦岛6 个市以及海洋经济发展所依托的相关陆域,规划期限为2021 年至2025 年,展望到2035 年。辽宁省作为中国最北沿海省份,拥有2292.4 公里海岸线(如图1 所示)。
在“海洋强省”建设目标的背景下,完成海洋经济发展规划的目标重在海洋高新技术领域创新。其中关键核心技术之一是攻克水下导航与定位的适配区分类预测技术。
水下航行器在执行水下任务时需要保持自主、无源、高隐蔽性、不受地域和时域限制、高精度的导航与定位。重力辅助导航是满足上述条件的主要方法之一。 在重力辅助导航系统中,影响导航可靠性与精度的关键步骤是选择匹配性高的航行区域,即适配区。适配区的标定与识别技术是最具挑战性的问题之一。选取适配区前需要对研究海域的重力基准图(基础性的是重力异常基准图)进行插值加密处理,基于重力基准图所提供水下航行器航行区域的重力异常变化情况对适配区的选取进行分析。
重力异常(值)的定义为:实际地球内部的物质密度分布不均匀,导致实际观测重力值与理论上的正常重力值总存在偏差,在排除各种干扰因素影响后,仅仅由地球物质密度分布不匀所引起的重力的变化,简称为重力异常。
在重力异常变化显著区域,导航系统可获得高的定位精度;反之,在重力异常变化平坦区域,导航系统会出现定位精度的不敏感。由于不同区域的重力异常特征分布不同,建立可行的适配区分类预测模型,对保障水下航行器的导航精度至关重要。
假设X 为影响区域匹配性的特征属性指标,Y 为刻画区域适配性的输出结果, F 为以X 为输入以Y 为输出的分类预测系统。
基于上述背景分析,请参考附件中的重力异常数据建立数学模型,解决以下问题:
问题一:附件1,给出一组分辨率为1’×1’(相邻两格网点间的距离是1’)的重力异常基准数据A,试通过精细化基准图,合理划分区域,完成各区域的适配性标定(标签Y )。
问题二:根据问题一中各划分区域的适配性标定结果Y ,合理选择区域的特征属性指标(特征X ),试建立有效的区域适配区分类预测模型(系统F )。
问题三:利用附件二中的重力异常基准数据B,试对问题二所建立的系统F进行迁移性预测并讨论该系统F 对新重力异常数据的适用性。
目录:(完整代码和论文见文末)
一、 摘要.... 1
二、 问题重述.... 3
三、 问题分析.... 4
3.1 问题一分析..... 4
3.2 问题二分析..... 4
3.3 问题三分析..... 4
四、 模型假设.... 5
五、 符号说明.... 6
六、 模型的建立和求解.... 6
6.1 问题一模型的建立和求解.... 6
6.1.1数据可视化.... 6
6.1.2 K均值聚类方法:.... 7
6.1.3 聚类求解结果.... 10
6.2 问题二模型的建立和求解.... 11
6.2.1 随机森林算法.... 11
6.2.2 决策树算法.... 12
6.2.3 SVM算法.... 13
6.2.4 使用其他多种分类方法.... 16
6.2.5 不同模型的比较.... 17
6.3 问题三模型的建立和求解.... 19
6.3.1 重力异常数据进行可视化.... 19
6.3.2 迁移预测.... 20
6.3.3 重力异常数据的适用性评估.... 21
七、 模型的评价.... 22
7.1 模型的优缺点.... 22
三、 问题分析
要建立一个数学模型来解决2023辽宁省数学建模竞赛B题,可以采用机器学习或统计分析的方法来完成重力异常数据的区域适配性标定。步骤如下:
3.1 问题一分析
数据准备:
导入附件1中的数据(经度、纬度、重力异常值)。 可能需要对数据进行预处理,如数据清洗,处理缺失值,进行标准化等。 特征工程:
可以考虑根据经度和纬度创建额外的特征,如距离某个地理坐标点的距离等。
标定区域适配性标签Y:
为了标定区域的适配性标签Y,需要定义一种方法来将数据点分为不同的区域或类别。这是一个无监督学习问题,可以考虑使用聚类分析(如K均值聚类)来将数据点分成不同的区域。
3.2 问题二分析
分类预测模型建立:
选择合适的机器学习模型,如决策树、随机森林、支持向量机、神经网络等,来预测区域适配性标签Y。 划分数据集为训练集和测试集,用训练集来训练模型,然后用测试集来评估模型的性能。 模型评估:
使用合适的性能指标(如准确度、召回率、F1分数等)来评估模型的性能。 可能需要进行交叉验证以确保模型的稳定性和泛化能力。
3.3 问题三分析
模型应用:
一旦模型建立并评估成功,可以使用该模型来预测附件2中的重力异常数据的区域适配性标签Y。
四、 模型假设
五、 符号说明
以下是问题1、问题2和问题3中需要使用的模型符号及其说明的总结

六、 模型的建立和求解
6.1 问题一模型的建立和求解
6.1.1 数据可视化
使用Python的matplotlib库对2023辽宁省数学建模竞赛B题数据驱动的水下导航适配区分类预测问题一进行数据可视化,然后使用K均值聚类进行数据点分区。
# 设置中文字体
plt.rcParams['font.sans-serif'] = 'SimHei' # 使用中文字体(这里使用的是“黑体”)
plt.rcParams['axes.unicode_minus'] = False # 用于正常显示负号# 可视化数据
plt.scatter(data['经度'], data['纬度'], c=data['重力异常值'], cmap='viridis')
plt.xlabel('经度')
plt.ylabel('纬度')
plt.title('重力异常数据分布')
plt.colorbar(label='重力异常值')
plt.savefig('gravity_anomaly_visualization.png', dpi=300)
plt.show()
6.1.2 K均值聚类方法
K均值聚类是一种无监督学习方法,用于将数据点分成K个不同的簇,以使每个数据点属于最近的簇。该方法的目标是最小化数据点与其所属簇中心之间的距离的总和。K均值聚类的算法如下:
选择K个初始簇中心,可以随机选择或根据某种启发式方法选择。
将每个数据点分配到与其最近的簇中心。
更新每个簇的中心,计算每个簇中所有数据点的平均值。
重复步骤2和步骤3,直到簇中心不再发生显著变化或达到预定的迭代次数。

(完整代码见文末)
# 使用K均值聚类
X = data[['经度', '纬度', '重力异常值']]
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X) # 标准化数据# 设置聚类数(这里设置为3,你可以根据实际情况调整)
kmeans = KMeans(n_clusters=3, random_state=0)# 保存包含区域标签的数据
data.to_excel('附件1_重力异常数据带区域标签.xlsx', index=False)
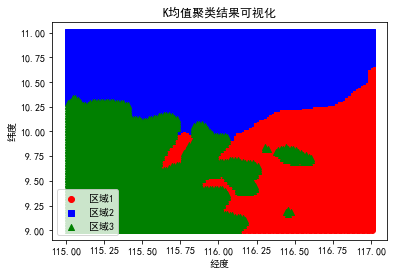
6.1.3 聚类求解结果
# 可视化不同区域的数据
plt.scatter(region1['经度'], region1['纬度'], label='区域1', c='red', marker='o')
plt.scatter(region2['经度'], region2['纬度'], label='区域2', c='blue', marker='s')
...plt.xlabel('经度')
plt.ylabel('纬度')
plt.title('K均值聚类结果可视化')
plt.legend()
plt.savefig('kmeans_clustering_result.png', dpi=300)
plt.show()
上述代码将可视化数据分布,并将其保存为名"gravity_anomaly_visualization.png"的图像。然后,它使用K均值聚类将数据点分为3个不同的区域,并将带有区域标签的数据保存为一个新的Excel文件。可以根据需要更改聚类数或其他参数以获得更合适的结果 。
1.1 问题二模型的建立和求解
2023辽宁省数学建模B题问题二:根据问题一中各划分区域的适配性标定结果Y ,合理选择区域的特征属性指标(特征X ),试建立有效的区域适配区分类预测模型(系统F )。
为了建立一个有效的区域适配区分类预测模型,可以采用监督学习方法,例如决策树、随机森林、支持向量机等,来预测区域的适配性标定结果Y
完整论文和代码:2023辽宁省数学建模高质量原创论文代码成品分享
这篇关于2023年辽宁省数学建模竞赛B题思路详细分析的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







