本文主要是介绍20210414_24期_集成学习(中)_Task08_bagging的原理和案例分析,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
八、bagging的原理和案例分析

目录
- 八、bagging的原理和案例分析
- 来源
- 8.1 Bagging
- 8.1.1 Bagging概念原理
- 9.1.2 Bagging流程
- 9.1.2 Bagging算法特点:
- 9.1.3 随机森林
- 8.2 Bagging的例子
- 参考资料
来源
Datewhle24期__集成学习(中) :
https://github.com/datawhalechina/team-learning-data-mining/tree/master/EnsembleLearning
作者:李祖贤、薛传雨、赵可、杨毅远、陈琰钰
论坛地址:
http://datawhale.club/t/topic/1574
8.1 Bagging
8.1.1 Bagging概念原理
-
首先一张靶图回顾下方差(Variance)和偏差(Bias):

Bias和Variance分别代表准和确两个概念。 -
Bagging是一种降低方差的技术
-
Bagging是Bootstrap aggregating的缩写。中文意思是自助聚合。而Bootstrap本身是一种有放回的抽样方法(可能抽到重复的样本)
-
Bagging是一种并行式的集成学习方法,即基学习器的训练之间没有前后顺序可以同时进行,Bagging使用**“有放回”采样的方式选取训练集**,对于包含m个样本的训练集,进行m次有放回的随机采样操作,从而得到m个样本的采样集,这样训练集中有接近36.8% [1] 的样本没有被采到。按照相同的方式重复进行,我们就可以采集到T个包含m个样本的数据集,从而训练出T个基学习器,最终对这T个基学习器的输出进行结合。
lim m ↦ ∞ ( 1 − 1 m ) m ↦ 1 e ≈ 0.368 \lim _{m \mapsto \infty}\left(1-\frac{1}{m}\right)^{m} \mapsto \frac{1}{e} \approx 0.368 m↦∞lim(1−m1)m↦e1≈0.368… [1]
9.1.2 Bagging流程
Bagging算法的流程:

- 另一形式:

- 从原始样本集中有放回随机采样。共进行k轮抽取,得到k个训练集。(bootstrap的过程,由于是有放回抽样,所以k个训练集之间相互独立)
- 每次使用一份训练集训练一个模型,k 个训练集共得到 k 个基模型。(注:这里并没有具体的分类算法或回归方法,我们可以根据具体问题采用不同的分类或回归方法,如决策树、感知器等)
- 利用这k个基模型对测试集进行预测,将k个预测结果进行聚合。(aggregating的过程)
1. 分类问题:将上步得到的k个模型采用投票的方式得到分类结果
2. 回归问题:计算上述模型的均值作为最后的结果。(所有模型的重要性相同)
9.1.2 Bagging算法特点:
1、可并行的集成方法。每个基模型可以分别、独立、互不影响地生成。
2、主要降低 Variance,对 Bias 无明显作用。因此,适用于 High Variance & Low Bias 的模型。
- 偏差角度:Bagging后的偏差与单个模型相近。
由于 B i a s = 1 k ∑ i = 1 k b i a s i Bias=\frac{1}{k} \sum_{i=1}^{k}bias_{i} Bias=k1∑i=1kbiasi( 共k个基模型, b i a s i bias_{i} biasi为第 i i i个基模型的偏差),所以 Bagging后的偏差与单个模型相近。 - 方差角度
- 方差有两个重要的性质,如下:
1、c为常数,则:
Var ( c X ) = E [ ( c X − E [ c X ] ) 2 ] = c 2 E [ ( X − E [ X ] ) 2 ] = c 2 Var ( X ) \operatorname{Var}(c X)=E\left[(c X-E[c X])^{2}\right]=c^{2} E\left[(X-E[X])^{2}\right]=c^{2} \operatorname{Var}(X) Var(cX)=E[(cX−E[cX])2]=c2E[(X−E[X])2]=c2Var(X)
2、独立随机变量之和的方差等于各变量的方差之和:
Var ( X 1 + ⋯ + X n ) = Var ( X 1 ) + ⋯ + Var ( X n ) \operatorname{Var}\left(X_{1}+\cdots+X_{n}\right)=\operatorname{Var}\left(X_{1}\right)+\cdots+\operatorname{Var}\left(X_{n}\right) Var(X1+⋯+Xn)=Var(X1)+⋯+Var(Xn)
如果各模型独立,根据1,2可知,整体方差:
Var ( 1 n ∑ i = 1 n X i ) = 1 n 2 Var ( ∑ i = 1 n X i ) = σ 2 n \operatorname{Var}\left(\frac{1}{n} \sum_{i=1}^{n} X_{i}\right)=\frac{1}{n^{2}} \operatorname{Var}\left(\sum_{i=1}^{n} X_{i}\right)=\frac{\sigma^{2}}{n} Var(n1i=1∑nXi)=n21Var(i=1∑nXi)=nσ2
因此Bagging可以减少方差。
9.1.3 随机森林
随机森林(Random Forest是Bagging的一个拓展体,它的基学习器固定为决策树,多棵树也就组成了森林,而“随机”则在于选择划分属性的随机,随机森林在训练基学习器时,也采用有放回采样的方式添加样本扰动,同时它还引入了一种属性扰动,即在基决策树的训练过程中,在选择划分属性时,RF先从候选属性集中随机挑选出一个包含K个属性的子集,再从这个子集中选择最优划分属性,一般推荐K=log2(d)。
这样随机森林中基学习器的多样性不仅来自样本扰动,还来自属性扰动,从而进一步提升了基学习器之间的差异度。相比决策树的Bagging集成,随机森林的起始性能较差(由于属性扰动,基决策树的准确度有所下降),但随着基学习器数目的增多,随机森林往往会收敛到更低的泛化误差。同时不同于Bagging中决策树从所有属性集中选择最优划分属性,随机森林只在属性集的一个子集中选择划分属性,因此训练效率更高。

8.2 Bagging的例子
-
案例来源: Amica的https://www.jianshu.com/p/c4bf8821af19集成方法-Bagging
-
数据集来自UCI网站中乳腺癌数据:
- 数据9个特征及因变量(诊断结果)
| 特征名称 | 数值范围 |
|---|---|
| Clump Thickness(肿块密度) | 1 - 10 |
| Uniformity of Cell Size(细胞大小均匀性) | 1-10 |
| Uniformity of Cell Shape(细胞形状均匀性) | 1-10 |
| Marginal Adhesion(边界黏连) | 1-10 |
| Single Epithelial Cell Size(单个上皮细胞大小) | 1-10 |
| Bare Nuclei(裸核) | 1-10 |
| Bland Chromatin(微受激染色质) | 1-10 |
| Normal Nucleoli(正常核) | 1-10 |
| Mitoses(有丝分裂) | 1-10 |
| Class(诊断结果) | 2表示良性, 4表示恶性 |
import numpy as np
import pandas as pd
data = pd.read_excel(r'C:\Users\GJX\Desktop\Datawhale-学习\23期\集成学习\乳腺癌数据集.xlsx')
data.head()
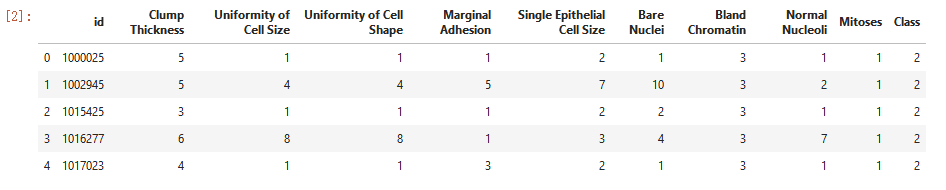
data.shape
(699, 11)
data.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 699 entries, 0 to 698
Data columns (total 11 columns):
id 699 non-null int64
Clump Thickness 699 non-null int64
Uniformity of Cell Size 699 non-null int64
Uniformity of Cell Shape 699 non-null int64
Marginal Adhesion 699 non-null int64
Single Epithelial Cell Size 699 non-null int64
Bare Nuclei 699 non-null object
Bland Chromatin 699 non-null int64
Normal Nucleoli 699 non-null int64
Mitoses 699 non-null int64
Class 699 non-null int64
dtypes: int64(10), object(1)
memory usage: 60.2+ KB
- 可以看出除了ID外, 数据有699个样本和9个特征, 且其中Bare Nuclei (裸核)可能存在缺失值:
data['Bare Nuclei'].value_counts()
1 402
10 132
5 30
2 30
3 28
8 21
4 19
? 16
9 9
7 8
6 4
Name: Bare Nuclei, dtype: int64
- 存在’?'的缺失值
data['Bare Nuclei'].replace('?',4, inplace=True)
data['Bare Nuclei'].value_counts()
1 402
10 132
4 35
5 30
2 30
3 28
8 21
9 9
7 8
6 4
Name: Bare Nuclei, dtype: int64
- 使用平均值替代裸核的缺失值
- 完成预处理后可利用决策树模型查看bagging的效果:
X=data.drop("Class",axis=1)
y=data.Class
#划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y,test_size=0.4, random_state=1)
#采用决策时模型作为基分类器,并采用熵作为指标对属性进行划分
tree = DecisionTreeClassifier(criterion='entropy', max_depth=None)#通过装袋集成方法生成500个决策树
bag = BaggingClassifier(base_estimator=tree,n_estimators=500,max_samples=1.0,max_features=1.0, bootstrap=True,bootstrap_features=False, n_jobs=1, random_state=1)
tree = tree.fit(X_train, y_train)
y_train_pred = tree.predict(X_train)
y_test_pred = tree.predict(X_test)
#准确
tree_train_accuracy = accuracy_score(y_train, y_train_pred)
tree_test_accuracy = accuracy_score(y_test, y_test_pred)
#召回 恶性 或者说灵敏度
tree_train_sen = recall_score(y_train, y_train_pred,pos_label=4)
tree_test_sen = recall_score(y_test, y_test_pred,pos_label=4)
#召回 良性 或者说特异性
tree_train_spe = recall_score(y_train, y_train_pred,pos_label=2)
tree_test_spe = recall_score(y_test, y_test_pred,pos_label=2)
print('Decision tree train/test accuracies(准确率) %.3f/%.3f' % (tree_train_accuracy , tree_test_accuracy ))
print('Decision tree train/test sen(灵敏度) %.3f/%.3f' % (tree_train_sen, tree_test_sen ))
print('Decision tree train/test spe(特异性) %.3f/%.3f' % (tree_train_spe, tree_test_spe ))
Decision tree train/test accuracies(准确率) 1.000/0.954
Decision tree train/test sen(灵敏度) 1.000/0.925
Decision tree train/test spe(特异性) 1.000/0.968
- bagging效果:
# 2、评估通过bagging集成的分类器性能#通过训练集训练多个决策树集成的模型
bag = bag.fit(X_train, y_train)
#运用bagging集成的模型预测训练集的类别
y_train_pred = bag.predict(X_train)
y_test_pred = bag.predict(X_test)#准确率
bag_train_accuracy = accuracy_score(y_train, y_train_pred)
bag_test_accuracy = accuracy_score(y_test, y_test_pred)#灵敏度
bag_train_sen = recall_score(y_train, y_train_pred,pos_label=4)
bag_test_sen = recall_score(y_test, y_test_pred,pos_label=4)#特异性
bag_train_spe = recall_score(y_train, y_train_pred,pos_label=2)
bag_test_spe = recall_score(y_test, y_test_pred,pos_label=2)#打印出集成模型在训练集和测试集上的准确率、灵敏度、特异性
print('Bagging train/test accuracies(准确率) %.3f/%.3f' % (bag_train_accuracy, bag_test_accuracy))
print('Bagging train/test sen(灵敏度) %.3f/%.3f' % (bag_train_sen, bag_test_sen ))
print('Bagging train/test spe(特异性) %.3f/%.3f' % (bag_train_spe, bag_test_spe ))
Bagging train/test accuracies(准确率) 1.000/0.964
Bagging train/test sen(灵敏度) 1.000/0.946
Bagging train/test spe(特异性) 1.000/0.973
- 明显三个指标都提升
参考资料
- https://zhuanlan.zhihu.com/p/37730184 从0开始机器学习-Bagging和Boosting
- https://www.heywhale.com/mw/project/5e4fbed50e2b66002c1fa4ac西瓜书学习笔记(9)–集成学习
- https://www.jianshu.com/p/c4bf8821af19集成方法-Bagging
这篇关于20210414_24期_集成学习(中)_Task08_bagging的原理和案例分析的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





