算法C4补题记录

本文主要是介绍算法C4补题记录，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

A 普通的活动安排

第一行包含一个整数 $n (1 \leq n \leq 106)$ 。
接下来 $n$ 行，每行两个整数 $x_i,y_i(1≤x_i<y_i≤105)$ ，表示每个项目的开始时间和结束时间。
输出一行一个整数，表示最多可以游玩的项目数。

贪心，希望剩下的时间越多越好，按活动结束时间排序。

#include <stdio.h>
#include <stdlib.h>
int n, a[1000005][2], i, now = 1, cnt;
int cmp(const void *p1, const void *p2)
{int *m = (int *)p1, *n = (int *)p2;if (*(m + 1) != *(n + 1)){return *(m + 1) - *(n + 1);}return *(m) - *(n);
}
int main()
{scanf("%d", &n);for (i = 0; i < n; i++){scanf("%d%d", &a[i][0], &a[i][1]);}qsort(a, n, 8, cmp);for (i = 0; i < n; i++){if (a[i][0] < now){continue;}else{now = a[i][1];cnt++;}}printf("%d", cnt);
}

B 钢条切割

需要 $N$ 根钢条，第 $i$ 根钢条的长度应该是 $L_i$ 。他订购了一根很长的钢条，长度就是这 $N$ 条钢条的总长度，每次开机都要收加工费，加工费用是需要锯开的钢条长度的两倍。比如要把一段长 3 米的钢条锯开，就要收 6 元。
设计一个锯开钢条的方案，使得付出的加工费之和最小。
输入
第一行：单个整数 $N ， 1 \leq N \leq 20000$
第二行到第 $N + 1$ 行：第 $i + 1$ 行有一个整数 $L_i，1≤L_i≤50000$
输出
单个整数：表示付出的最小费用

这题真是太让我受益匪浅了，用小顶堆模拟哈夫曼树。
需要切割成本最小，直观来讲，就是先切大块，后切小块，越长的部分越先切除，越少切，避免留着害事。这就是在模拟哈夫曼树，权重越大的结点离根节点越近，最后的成本就是非叶子节点频率*2。

哈夫曼树手写太男了，所以用优先队列来实现。和构建哈夫曼树的过程一样，先取两个最小的元素，加起来放入队列中，直到只剩一个节点。
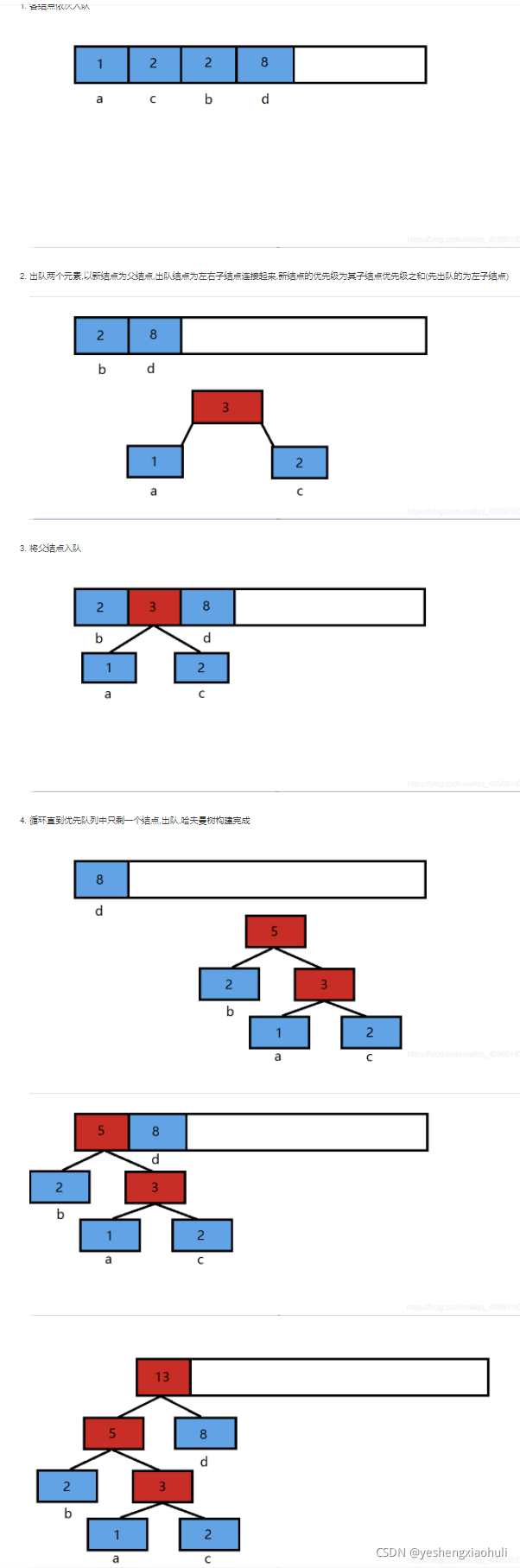
在这里插入图片描述
那么就是，长度为13的，分割成5和8，5分割成2和3，3分割成1和2，分割的都是非叶子节点。

#include <iostream>
#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <algorithm>
#include <queue>
using namespace std;
struct data
{int x, y, z;bool operator<(const data &o) const{return o.z < z;}
};
int main()
{int n, cnt;long long money = 0;scanf("%d", &n);cnt = n;priority_queue<int, vector<int>, greater<int> /*这两个 >之间一定要加一个空格*/> q;for (int i = 1; i <= n; i++){int x;scanf("%d", &x);q.push(x);}while (cnt > 1){int x, y;x = q.top();q.pop();y = q.top();q.pop();//printf("%d %d\n", x, y);q.push(x + y);cnt--;money += 2 * (x + y);}printf("%lld\n", money);return 0;
}

这个板子还不是很懂，改天再看。

C 等差数列构造

出一个长度为3的非负整数数列 $a, b, c$ 。对这个数列，可以执行这样一种操作：选择一个数，让它的值变为原来的值+1。

问最少执行几次操作后，这个数列可以变成等差数列，也就是 $b - a = c - b$ 。

#include <iostream>
#include <algorithm>
using namespace std;
long long a[3];
int main()
{cin >> a[0] >> a[1] >> a[2];long long x = a[2] - a[1], y = a[1] - a[0];if (x > y)cout << (((x - y) & 1) ? (x - y + 1) / 2 + 1 : (x - y) / 2);elsecout << y - x;
}

如果左边的距离大于右边的距离，直接往 $a$ 上加就可以。
比如 $a = 2, b = 10, c = 12$
除了往a上加也不能做什么了。

如果两段距离差是偶数。
$a = 2, b = 4, c = 12$
那就往上加 $b$ ，加到平均分的位置。
如果两端距离差是奇数，如
$a = 3, b = 4, c = 12$
对a,c取平均不再是整数了，先把a往上加1，b再取平均。

D 出路

给定一个矩阵，问你从起点走到终点有多少种走法。起点为左上角，终点为右下角，要求只能向右走一格或向下走一格。#表示不可停留，.表示可以停留，保证左上角和右下角为.，要求结果对1000000007取模。

普通的dp，连我都会做。

#include <stdio.h>
int ans, n, m, i, j;
char x[5], xx;
int road[105][105];
int c[105][105];
int N = 1000000007;
int main()
{scanf("%d%d", &n, &m);gets(x);for (i = 0; i < n; i++){for (j = 0; j < m; j++){scanf("%c", &xx);if (xx == '#'){road[i][j] = 1;}}gets(x);}c[0][0] = 1;for (i = 0; i < n; i++){c[i][0] = 1;if (road[i][0] == 1){c[i][0] = 0;break;}}for (i = 0; i < m; i++){c[0][i] = 1;if (road[0][i] == 1){c[0][i] = 0;break;}}for (i = 1; i < n; i++){for (j = 1; j < m; j++){c[i][j] = (c[i][j - 1] % N + c[i - 1][j] % N) % N;if (road[i][j] == 1){c[i][j] = 0;}}}printf("%d", c[n - 1][m - 1]);
}

到一个格子，可能是从左边来的，也可能是从上边来的。
C[i][j]：到格子(i，j)的方案数.
$C [i] [j] = (c [i] [j - 1] + c [i - 1] [j]);$
如果左（上）边的格子不能踩，那肯定不能从那个方向过来，直接把到左边（上面）格子的方案数置0就可以。

E 数列划分

是贪心，我随便写的，不会证，再说吧。

F 故障的打印机

字符串dp，连我都会。

在机房里有一台打印机，因为年久失修，所以在打印东西时有一定概率发生故障。具体的说，当打印机在打印英文字母时，可能会将一个 $w$ 字母打印成 $u u$ ，也可能将一个 $m$ 字母打印成 $n n$ 。

现在，给出一段打印机的打印结果，请求出原文一共有多少种可能。由于答案可能很大，所以只需要输出其对 $1000000007$ 取模的结果。

#include <stdio.h>
#include <string.h>
char s[100005];
int dp[100005];
int N = 1000000007;
int len, i, j, k;
int main()
{scanf("%s", s);len = strlen(s);dp[0] = 1;if (s[0] == 'u' && s[1] == 'u' || s[0] == 'n' && s[1] == 'n'){dp[1] = 2;}else{dp[1] = 1;}for (i = 2; i < len; i++){if (s[i] == 'u' && s[i - 1] == 'u' || s[i] == 'n' && s[i - 1] == 'n'){dp[i] = (dp[i - 1] % N + dp[i - 2] % N) % N;}else{dp[i] = dp[i - 1];}}printf("%d", dp[len - 1]);
}

如果这个和上一个都是“u”或“v”：
$d p [i] = (d p [i - 1] + d p [i - 2])$
dp[i - 1]代表不犯错，dp[i - 2]代表犯错了，直接把这个和上个连在一起看成一个字符了。

G 单周期CPU

有两个正整数数列 A 和 B，每个数列都有 n 个互不相同的元素，不妨假设为a1,a2…an和b1,b2…bn。可以任意次交换数列 A 中两个元素的位置，求 $Π_{i=1}^n=a_i^{b_i}$ 的最大值。

然后重新排列了A，得到了以上最大值。

然后又重新排列了数列 B 中的元素（注意，并没有动已经交换好的A数列），现在 $Π_{i=1}^n=a_i^{b_i}$ 的值是最小的了。

求重新排列数列 B 后，数列 B 的样子。可以证明，这道题不需要给出A数列。

对原数列换个顺序，最大的和最小的交换一下，第二大的和第二小的交换…

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
int n, i;
int b[100005];
int c[100005];
int hash[10000005];
int cmp(const void *p1, const void *p2)
{int *m = (int *)p1;int *n = (int *)p2;return *m - *n;
}int main()
{scanf("%d", &n);memset(hash, -1, sizeof(hash));for (i = 0; i < n; i++){scanf("%d", &b[i]);c[i] = b[i];}qsort(b, n, 4, cmp);int left = 0, right = n - 1;while (left <= right){hash[b[left]] = b[right];hash[b[right]] = b[left];left++;right--;}for (i = 0; i <= n - 1; i++){printf("%d ", hash[c[i]]);}
}

快排，然后while (left <= right)，用哈希表记录
$h a s h [应该输出这个数] = 输出那个数$
然后用拷贝的原数列，照着哈希表进行输出。

H 1082逐差法

本来有 n 个实验数据 d1,d2…dn。

每次逐差会从当前的数据中拿出两个数据，然后用大的数据减去小的数据，并将这个结果重新加入实验数据中。

也就是说每次逐差，实验数据的数目就会减 1。

当只剩一个实验数据时停止逐差。

求一个取数方案，使得最后剩的这个实验数据的值最小。

此问题可以转化为给定数组组成一个表达式，各个位置可以自选正负，计算最终结果为正数的最小
值。
设所有带正号的元素在 $P$ 集合中，和为 $s 1$ ,所有带负号的元素在 $Q$ 集合中，和为 $s 2$ ，设整个数组的和为 $s u m$ ，则 $s 1 + s 2 = s u m$ ，设 $s 1 - s 2 = a n s$ ，则 $a n s = s u m - 2 * s 2$ ，只要求在 $s u m / 2$ 以下最大的 $s 2$ 即可。
所以可以转化为01背包问题：有 $n$ 件物品，重量和价值都为 $d_i$ ，背包最大容积为 $s u m / 2$ ，求最终能装下的最大价值。

#include<cstdio>
#include<iostream>
using namespace std;
int n, a[505], dp[500005], sum;
int main()
{cin >> n;for(int i = 1; i <= n; i++)cin >> a[i], sum += a[i];for(int i = 1; i <= n; i++)for(int j = sum / 2; j >= a[i]; j--)dp[j] = max(dp[j], dp[j-a[i]] + a[i]);cout << sum - dp[sum/2]*2;
}